2022年浙教版数学七下期中复习阶梯训练：整式的乘除（优生加练）

试卷更新日期：2022-04-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知a=8³³ ， b=16²⁵ ， c=32¹⁹ ，则有（）

A、a<b<c B、c<b<a C、c<a<b D、a<c<b

查看试题解析
2. 如图有两张正方形纸片A和B ，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（）

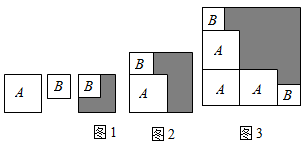A、22 B、24 C、42 D、44

查看试题解析
3. 如图1的8张宽为a，长为 $b (a < b)$ 的小长方形纸片，按如图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示.设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）

A、 $b = 5 a$ B、 $b = 4 a$ C、 $b = 3 a$ D、 $b = a$

查看试题解析
4. 为了求 $1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}$ 的值，可设 $s = 1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}$ ，等式两边同乘以 $2$ ，得 $2 s = 2 (1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}) = 2 + 2^{2} + 2^{3} + \dots + 2^{51}$ ，所以得 $2 s - s = (2 + 2^{2} +$ $2^{3} + \dots + 2^{51}) - (1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}) = 2^{51} - 1$ ，所以 $s = 2^{51} - 1$ ，即： $1 + 2 + 2^{2} + 2^{3} +$ $\dots + 2^{50}$ ＝ $2^{51} - 1$ .仿照以上方法求 $1 + 5 + 5^{2} + 5^{3} + \dots + 5^{2020}$ 的值为（）

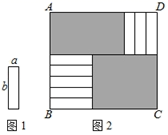A、 $5^{2021} - 1$ B、 $5^{2020} - 1$ C、 $\frac{5^{2020} - 1}{4}$ D、 $\frac{5^{2021} - 1}{4}$

查看试题解析
5. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
6. 如图，有A，B，C三种不同型号的卡片，每种各10张.A型卡片是边长为a的正方形，B型卡片是相邻两边长分别为a、b的长方形，C型卡片是边长为b的正方形.从中取出若干张卡片（每种卡片至少一张），把取出的这些卡片拼成一个正方形，所有符合要求的正方形的个数是（）

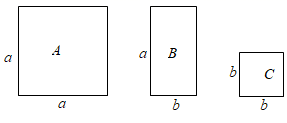A、4 B、5 C、6 D、7

查看试题解析
7. 如图，有两个正方形A ， B ，现将B放在A的内部得图甲，将A ， B并列放置后构造新的正方形得图乙。若图甲和图乙中阴影部分的面积分别为3和30，则正方形A、B的面积之和为（）

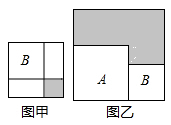A、33 B、30 C、27 D、24

查看试题解析
8. 若 $3^{x} + 3^{x} + 3^{x} + 3^{x} = \frac{4}{9}$ ，则 $x =$ （）

A、-2 B、-1 C、0 D、 $\frac{1}{4}$

查看试题解析
9. 已知a＝2019x+2018，b＝2019x+2019，c＝2019x+2020．则多项式a²+b²+c²﹣ab﹣bc﹣ac的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
10. 观察下列各式及其展开式：（）
${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$

${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$

${(a + b)}^{5} = a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$

……

你猜想 ${(a + b)}^{10}$ 的展开式第三项的系数是（）

A、66 B、55 C、45 D、36

查看试题解析

二、填空题

11. 用纸片拼图时，我们发现利用图1中的三种纸片（边长分别为 $a$ ， $b$ 的正方形和长为 $b$ 宽为 $a$ 的长方形）各若干，可以拼出一些长方形来解释某些等式，比如图2可以解释为： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ．

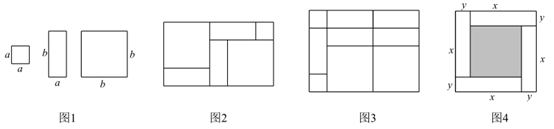(1)、图3可以解释为等式：；

(2)、要拼出一个两边长为 $a + b$ ， $3 a + b$ 的长方形，先回答需要以下三种纸片各多少块，再用画图或整式乘法验证你的结论；
块，块，块

(3)、如图4，大正方形的边长为 $m$ ，小正方形的边长为 $n$ ，若用 $x$ ， $y$ （ $x > y$ ）表示四个相同小长方形的两边长，以下关系式正确的是（填序号）．① $x + y = m$ ；② $2 x y = m^{2} - n^{2}$ ；③ $x^{2} - y^{2} = m n$ ；④ $x^{2} + y^{2} = m^{2} + n^{2}$ ．

查看试题解析
12. 如图是一块长方形ABCD的场地，长AB=a米，宽AD=b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为米² ．

查看试题解析
13. 已知 $x 、 y > 0, x^{2} + y^{2} = 24, {(\sqrt{x} + \sqrt{y})}^{4} + {(\sqrt{x} - \sqrt{y})}^{4} = 180$ ，则 $x y$ = ．

查看试题解析
14. 若（x-3)^x=1，则x的值为.

查看试题解析
15. 如图，现有A，C两类正方形卡片和B类长方形卡片各若干张，用它们可以拼成一些新的长方形．如果要拼成一个长为（3a+b），宽为（a+2b）的长方形，那么需要B类长方形卡片张．

查看试题解析
16. 阅读材料后解决问题：
小明遇到下面一个问题：计算(2+1)(2²+1)(2⁴+1)(2⁸+1)。

经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：

(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1)=(2²-1)(2²+1)(2⁴+1)(2⁸+1)=(2⁴-1)(2⁴+1)(2⁸+1)=(2⁸-1)(2⁸+1)=2¹⁶-1

请你仿照小明解决问题的方法，尝试计算：(6+1)(6²+1)(6⁴+1)(6⁸+1)=。

查看试题解析

三、解答题

17. 若a=2⁵⁵ ， b=3⁴⁴ ， c=4³³ ， d=5²² ，试比较a，b，c，d的大小。

查看试题解析
18. 已知： $A = b y^{2} - a y - 1$ ， $B = 2 y^{2} + 3 a y - 10 y - 1$ ，且多项式 $2 A - B$ 的值与字母y的取值无关，求 $(2 a^{2} b + 2 a b^{2}) - [2 (a^{2} b - 1) + 3 a b^{2} + 2]$ 的值．

查看试题解析
19. 证明：两个连续奇数的平方差是8的倍数，并且等于这两个数的和的两倍．

查看试题解析
20. 已知16^m=4×2²ⁿ^﹣² ， 27ⁿ=9×3^m⁺³ ，求（n﹣m）²⁰¹⁰的值．

查看试题解析
21. 已知代数式：①4^β+1 ， ② $\frac{2}{4^{α}}$ ， ③﹣2，④0，又设k=2ⁿ且α，β，n为整数，
（1）讨论n的正负性，判断①、②、③、④这4个代数式中与k相等的可能性？
（2）进一步说明4^β+1与 $\frac{2}{4^{α}}$ 两个代数式相等的可能性．

查看试题解析
22. 已知α，β为整数，有如下两个代数式2^2α ， $\frac{2}{4^{β}}$
（1）当α=﹣1，β=0时，求各个代数式的值；
（2）问它们能否相等？若能，则给出一组相应的α，β的值；若不能，则说明理由．

查看试题解析

四、综合题

23. 运用所学知识，完成下列题目.

(1)、若 $2^{a} = 3 ， 2^{b} = 6 ， 2^{c} = 12$ ，直接说出a，b，c之间的数量关系：.

(2)、若 $2^{a} = 6 ， 4^{b} = 12 ， 16^{c} = 8$ ，试确定a，b，c之间的数量关系，并说明理由；

(3)、若 $a^{5} = 2 ， b^{5} = 3 ， c^{5} = 72$ ，试确定a，b，c之间的数量关系，并说明理由.

查看试题解析
24. 已知多项式 $x + 2$ 与另一个多项式 $A$ 的乘积为多项式 $B$ .

(1)、若 $A$ 为关于 $x$ 的一次多项式 $x + a ， B$ 中 $x$ 的一次项系数为0，直接写出 $a$ 的值；

(2)、若 $B$ 为 $x^{3} + p x^{2} + q x + 2$ ，求 $2 p - q$ 的值.

(3)、若 $A$ 为关于 $x$ 的二次多项式 $x^{2} + b x + c$ ，判断 $B$ 是否可能为关于 $x$ 的三次二项式，如果可能，请求出b，c的值；如果不可能，请说明理由.

查看试题解析
25. 实践与探索
如图1，边长为 $a$ 的大正方形有一个边长为 $b$ 的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）

(1)、上述操作能验证的等式是____；（请选择正确的一个）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ C、 $a^{2} + a b = a (a + b)$

(2)、请应用这个公式完成下列各题：
①已知 $4 a^{2} - b^{2} = 24$ ， $2 a + b = 6$ ，则 $2 a - b =$ ▲ ．
②计算： $10 0^{2} - 9 9^{2} + 9 8^{2} - 9 7^{2} + ⋯ + 4^{2} - 3^{2} + 2^{2} - 1^{2}$

查看试题解析
26. 嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张．

(1)、问题发现
他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②)．根据图形的面积关系写出一个你所熟悉的乘法公式，这个乘法公式是；

(2)、如果要拼成一个长为a＋2b ，宽为a＋b的大长方形，那么需要Ⅱ型卡片张，Ⅲ型卡片张．

(3)、拓展探究
若a＋b=5，ab=6，求a²＋b²的值；

(4)、当他拼成如图③所示的长方形时，根据图形的面积，可把多项式a²＋3ab＋2b²分解因式，其结果是．

(5)、解决问题
请你依照嘉嘉的方法，利用拼图分解因式：a²＋5ab＋6b²= ．

查看试题解析