2022年浙教版数学七下期中复习阶梯训练:平行线(优生集训)
试卷更新日期:2022-04-08 类型:复习试卷
一、综合题
-
1. 已知点C在射线OA上.
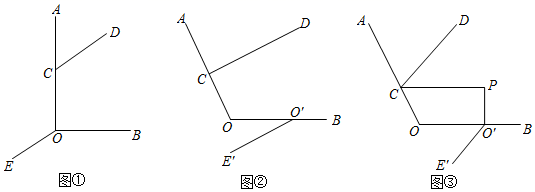 (1)、如图①,CD OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示)(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.2. 如图,直线 直线 ,一块三角板的顶点 在直线 上,边 、 分别交直线 于 、 两点. , , .
(1)、如图①,CD OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示)(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.2. 如图,直线 直线 ,一块三角板的顶点 在直线 上,边 、 分别交直线 于 、 两点. , , . (1)、如图1, ,则
(1)、如图1, ,则① ▲ °;
②若 与 的角平分线交于点 ,则 ▲ °.
(2)、如图2,点 在 的平分线上,连 ,且 ,若 ,求 的度数.(3)、如图3,若 , ,则 °(用含 的式子表示).3. 光线反射是一种常见的物理现象,在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机,自行车尾部的反光镜等就是应用了光的反射原理.
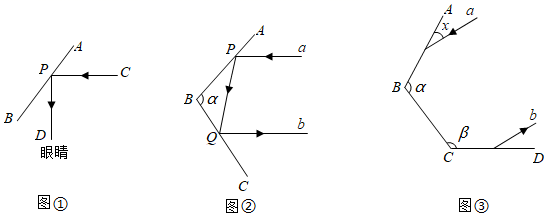 (1)、提词器的原理如图①,AB表示平面镜,CP表示入射光线,PD表示反射光线,∠CPD=90°,求∠APC的度数;(2)、自行车尾部的反光镜在车灯照射下,能把光线按原来的方向返回(如图②),a表示入射光线,b表示反射光线,a∥b.平面镜AB与BC的夹角∠ABC= ,求 .(3)、如图③,若 =108°,设平面镜CD与BC的夹角∠BCD= (90°< <180°),入射光线a与平面镜AB的夹角为x(0°<x<90°),已知入射光线a从平面镜AB开始反射,经过2或3次反射,当反射光线b与入射光线a平行时,请直接写出 的度数.(可用含x的代数式表示).4. (基础知识)(1)、古希腊七贤之一,著名哲学家泰勒斯(Thales , 公元前6世纪)最早从拼图实践中发现了“三角形内角和等于 ”,但这种发现完全是经验性的,泰勒斯并没有给出严格的证明.之后古希腊数学家毕达哥拉斯、欧几里得、普罗科拉斯等相继给出了基于平行线性质的不同的证明.其中欧几里得利用辅助平行线和延长线,通过一组同位角和内错角证明了该定理.请同学们帮助欧几里得将证明过程补充完整.
(1)、提词器的原理如图①,AB表示平面镜,CP表示入射光线,PD表示反射光线,∠CPD=90°,求∠APC的度数;(2)、自行车尾部的反光镜在车灯照射下,能把光线按原来的方向返回(如图②),a表示入射光线,b表示反射光线,a∥b.平面镜AB与BC的夹角∠ABC= ,求 .(3)、如图③,若 =108°,设平面镜CD与BC的夹角∠BCD= (90°< <180°),入射光线a与平面镜AB的夹角为x(0°<x<90°),已知入射光线a从平面镜AB开始反射,经过2或3次反射,当反射光线b与入射光线a平行时,请直接写出 的度数.(可用含x的代数式表示).4. (基础知识)(1)、古希腊七贤之一,著名哲学家泰勒斯(Thales , 公元前6世纪)最早从拼图实践中发现了“三角形内角和等于 ”,但这种发现完全是经验性的,泰勒斯并没有给出严格的证明.之后古希腊数学家毕达哥拉斯、欧几里得、普罗科拉斯等相继给出了基于平行线性质的不同的证明.其中欧几里得利用辅助平行线和延长线,通过一组同位角和内错角证明了该定理.请同学们帮助欧几里得将证明过程补充完整.已知:如图,在 中,

求证: .
证明:延长线段 至点 ,并过点 作 .
∵ (已作),
∴ ▲ (两直线平行,内错角相等),
▲ (两直线平行,同位角相等).
∵ ▲ (平角的定义),
∴ (等量代换).
(2)、(实践运用)如图1,线段 、 相交于点 ,连结 、 ,试证明: .证明:
 (3)、(变化拓展)
(3)、(变化拓展)

①如图2, 、 分别平分 、 ,若 , ,则 的度数为 ;
②如图3,直线 平分 , 平分 ,若 , ,则 的度数为 .
5. 如图1, 中,点 分别在 边上,且 ,点 是边 上一动点,过点 作 与线段 交于点 .(1)、求证: (2)、若点 在边 上运动,保证点 存在且不与点 重合.探究:当点 满足的怎样的位置条件, 成立?请在图2中画出符合条件的图形,并说明理由.
(2)、若点 在边 上运动,保证点 存在且不与点 重合.探究:当点 满足的怎样的位置条件, 成立?请在图2中画出符合条件的图形,并说明理由. (3)、在(2)的条件下,若 成立,直接写出 与ZEDH之间的数量关系6. 上学期我们利用三角板探究了两个角之间的关系,现在我们利用量角器来开展两角之间数量关系的探究活动.已知射线 ,连接AB,P是射线AM上的一个动点(不与点A重合).
(3)、在(2)的条件下,若 成立,直接写出 与ZEDH之间的数量关系6. 上学期我们利用三角板探究了两个角之间的关系,现在我们利用量角器来开展两角之间数量关系的探究活动.已知射线 ,连接AB,P是射线AM上的一个动点(不与点A重合). (1)、如图1,当PB平分 时,利用量角器探究发现 ,请说明理由.(2)、如图2,BC,BD分别平分 和 ,分别交射线AM于点C,D,利用量角器探究发现 与 之间的数量关系保持不变,请写出它们的关系,并说明理由.(3)、在(2)的条件下,点P继续在射线AM上运动,当运动到使 时,我们发现 与 之间存在某种数量关系,请你用含 的式子表示 .7. 已知 ∥ ,点 、 分别是 、 上的两点,点 在 、 之间,连接 、 .(1)、如图①,若 ,求 的度数;
(1)、如图1,当PB平分 时,利用量角器探究发现 ,请说明理由.(2)、如图2,BC,BD分别平分 和 ,分别交射线AM于点C,D,利用量角器探究发现 与 之间的数量关系保持不变,请写出它们的关系,并说明理由.(3)、在(2)的条件下,点P继续在射线AM上运动,当运动到使 时,我们发现 与 之间存在某种数量关系,请你用含 的式子表示 .7. 已知 ∥ ,点 、 分别是 、 上的两点,点 在 、 之间,连接 、 .(1)、如图①,若 ,求 的度数; (2)、如图②,若点 是 下方一点, 平分 , 平分 ,已知 ,求 的度数;
(2)、如图②,若点 是 下方一点, 平分 , 平分 ,已知 ,求 的度数; (3)、如图③,若点 是 上方一点,连接
(3)、如图③,若点 是 上方一点,连接 、 ,且 的延长线 平分 , 平分 , ,求 的度数.
、 ,且 的延长线 平分 , 平分 , ,求 的度数.  8. 已知:任何一个三角形都满足三角形三内角和等于 ,我们把这个结论称之为三角形三内角和定理.如图1, ,且 ,请根据题目条件,结合三角形三内角和定理,探究下列问题:
8. 已知:任何一个三角形都满足三角形三内角和等于 ,我们把这个结论称之为三角形三内角和定理.如图1, ,且 ,请根据题目条件,结合三角形三内角和定理,探究下列问题: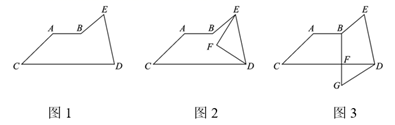 (1)、如图2,在图1基础上作: , , 与 交于点 ,求 的度数;(2)、如图3,在图1基础上作:过 作 ,交 于点 ,且 ,求 的值.9. 已知:AB∥CD .
(1)、如图2,在图1基础上作: , , 与 交于点 ,求 的度数;(2)、如图3,在图1基础上作:过 作 ,交 于点 ,且 ,求 的值.9. 已知:AB∥CD . (1)、探究∠B、∠BED、∠D之间的数量关系,并说明理由;(2)、利用上述中的结论,
(1)、探究∠B、∠BED、∠D之间的数量关系,并说明理由;(2)、利用上述中的结论,①如图2,已知AB∥CD , 试探究∠E、∠G、∠B、∠F、∠D之间的数量关系,并说明理由;
②如图3,已知AB∥CD , 请直接写出∠B、∠D、∠E1、∠E2……∠En、∠F1、∠F2…∠Fn+1之间的数量关系.
10. 直线 , 是 上一定点, 是直线 上一动点,点 在直线 , 之间,且 , , 的平分线交直线 于点 . (1)、如图1,若 ,则 的度数是°.(2)、如图2,若 ,求 的度数;(3)、若 的角平分线交 于点 ,求 的度数(用含 的式子表示).11. 如图1,已知直线CD∥EF , 点A , B分别在直线CD与EF上.P为两平行线间一点.
(1)、如图1,若 ,则 的度数是°.(2)、如图2,若 ,求 的度数;(3)、若 的角平分线交 于点 ,求 的度数(用含 的式子表示).11. 如图1,已知直线CD∥EF , 点A , B分别在直线CD与EF上.P为两平行线间一点. (1)、若∠DAP=40°,∠FBP=70°,则∠APB=(2)、猜想∠DAP , ∠FBP , ∠APB之间有什么关系?并说明理由;(3)、利用(2)的结论解答:
(1)、若∠DAP=40°,∠FBP=70°,则∠APB=(2)、猜想∠DAP , ∠FBP , ∠APB之间有什么关系?并说明理由;(3)、利用(2)的结论解答:①如图2,AP1 , BP1分别平分∠DAP , ∠FBP , 请你写出∠P与∠P1的数量关系,并说明理由;
②如图3,AP2 , BP2分别平分∠CAP , ∠EBP , 若∠APB=β,求∠AP2B . (用含β的代数式表示)
12. 已知 , 是截线 上的一点, 与 、 分别交于 、 .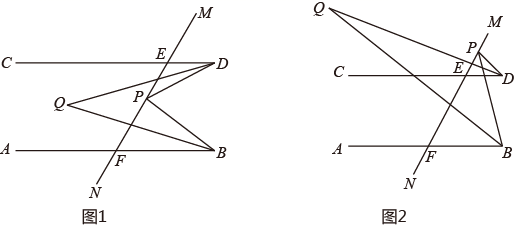 (1)、若 , ,求 的度数:(2)、如图1,当点 在线段 上运动时, 与 的平分线交于 ,问: 是否为定值?若是定值、请求出定值:若不是,说明其范围(3)、①如图2,当点 在线段 的延长线上运动时, 与 的平分线交于 ,则 的值为 ▲ .
(1)、若 , ,求 的度数:(2)、如图1,当点 在线段 上运动时, 与 的平分线交于 ,问: 是否为定值?若是定值、请求出定值:若不是,说明其范围(3)、①如图2,当点 在线段 的延长线上运动时, 与 的平分线交于 ,则 的值为 ▲ .②当点 在线段 上运动时, 与 的 等分线交于 ,其中 , ,设 ,求 的度数(直接用含 , 的代数式表示,不需说明理由).
13. 在三角形ABC中,点D在线段AC上,ED BC交AB于点E , 点F在线段AB上(点F不与点A , E , B重合),连接DF , 过点F作FG⊥FD交射线CB于点G .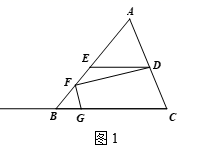

 (1)、如图1,点F在线段BE上,用等式表示∠EDF与∠BGF的数量关系,并证明;(2)、如图2,点F在线段BE上,求证:∠ABC+∠BFG-∠EDF=90°;(3)、当点F在线段AE上时,依题意,在图3中补全图形,请直接用等式表示∠EDF与∠BGF的数量关系,不需证明.14. 如图
(1)、如图1,点F在线段BE上,用等式表示∠EDF与∠BGF的数量关系,并证明;(2)、如图2,点F在线段BE上,求证:∠ABC+∠BFG-∠EDF=90°;(3)、当点F在线段AE上时,依题意,在图3中补全图形,请直接用等式表示∠EDF与∠BGF的数量关系,不需证明.14. 如图 (1)、问题情境:如图1,AB//CD , ∠PAB=130°,∠PCD=120°.求∠APC度数.
(1)、问题情境:如图1,AB//CD , ∠PAB=130°,∠PCD=120°.求∠APC度数.小明的思路是:如图2,过P作PE∥AB , 通过平行线性质,可得∠APC= .
(2)、问题迁移:如图3,AD//BC , 点P在射线OM上运动,∠ADP=∠α , ∠BCP=∠β .当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(3)、如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.15. 如图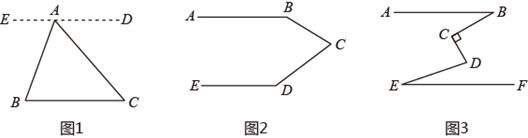 (1)、如图1,已知点A是BC上方的一点,连接AB,AC,求∠B+∠BAC+∠C的度数.
(1)、如图1,已知点A是BC上方的一点,连接AB,AC,求∠B+∠BAC+∠C的度数.阅读并补充下面的求解过程,
解:过点A画ED∥BC.
根据“”,可以得到∠B= , ∠C=∠DAC.
而∠EAB+∠BAC+∠DAC=180°,所以∠B+∠BAC+∠C=180°.
(2)、如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数(提示:过点C画CF∥AB).(3)、如图3,AB∥EF,BC⊥DC于点C,设∠B=x,∠D=y,∠E=z,请用一个含x,y,z的等式表示∠B,∠D,∠E三者之间的数量关系.(直接写出结果)16. 如图,直线PQ∥MN . (1)、若把一块三角尺( )按如图甲方式放置,点D , E , F是三角尺的边与平行线的交点,若 ,则 =度;(2)、若点C是PQ、MN之间(不在直线PQ , MN上)的一个点,且∠1与∠2都是锐角,如图乙,写出∠DCE与∠1,∠2之间的数量关系,并说明理由;(3)、将图甲中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG , 且有∠CEG=∠CEM , 求 的值.17. 我区防汛指挥部在一河道的危险地带两岸各安置一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A光射线自AM顺时针旋转至AN便立即逆时针旋转至AM,如此循环.灯B光射线自BP顺时针旋转至BQ便立即逆时针旋转至BP,如此循环.两灯交叉照射且不间断巡视.若灯A转动的速度是a度/秒,灯B转动的速度是b度/秒,且a,b满足(a﹣4b)2+(a+b﹣5)2=0.若这一带江水两岸河堤相互平行,即PQ∥MN,且∠BAN=60°.根据相关信息,解答下列问题.
(1)、若把一块三角尺( )按如图甲方式放置,点D , E , F是三角尺的边与平行线的交点,若 ,则 =度;(2)、若点C是PQ、MN之间(不在直线PQ , MN上)的一个点,且∠1与∠2都是锐角,如图乙,写出∠DCE与∠1,∠2之间的数量关系,并说明理由;(3)、将图甲中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG , 且有∠CEG=∠CEM , 求 的值.17. 我区防汛指挥部在一河道的危险地带两岸各安置一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A光射线自AM顺时针旋转至AN便立即逆时针旋转至AM,如此循环.灯B光射线自BP顺时针旋转至BQ便立即逆时针旋转至BP,如此循环.两灯交叉照射且不间断巡视.若灯A转动的速度是a度/秒,灯B转动的速度是b度/秒,且a,b满足(a﹣4b)2+(a+b﹣5)2=0.若这一带江水两岸河堤相互平行,即PQ∥MN,且∠BAN=60°.根据相关信息,解答下列问题.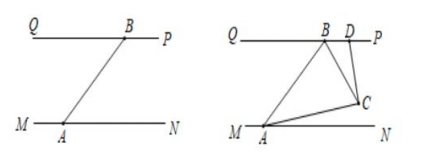 (1)、a= , b=.(2)、若灯B的光射线先转动24秒,灯A的光射线才开始转动,在灯B的光射线到达BQ之前,灯A转动几秒,两灯的光射线互相平行?(3)、如图2,若两灯同时开始转动照射,在灯A的光射线到达AN之前,若两灯射出的光射线交于点C,过点C作CD⊥AC交PQ于点D,则在转动的过程中,∠BAC与∠BCD间的数量关系是否发生变化?若不变,请求出这两角间的数量关系;若改变,请求出各角的取值范围.18. 已知直线AD∥EC,直线DE分别与AD,EC交于D,E两点,点B是直线DE上的一个动点,试探究∠ABC与∠1,∠2之间的数量关系.
(1)、a= , b=.(2)、若灯B的光射线先转动24秒,灯A的光射线才开始转动,在灯B的光射线到达BQ之前,灯A转动几秒,两灯的光射线互相平行?(3)、如图2,若两灯同时开始转动照射,在灯A的光射线到达AN之前,若两灯射出的光射线交于点C,过点C作CD⊥AC交PQ于点D,则在转动的过程中,∠BAC与∠BCD间的数量关系是否发生变化?若不变,请求出这两角间的数量关系;若改变,请求出各角的取值范围.18. 已知直线AD∥EC,直线DE分别与AD,EC交于D,E两点,点B是直线DE上的一个动点,试探究∠ABC与∠1,∠2之间的数量关系. (1)、如图①,当点B在线段DE上运动(点B不与D,E重合)时,若∠1=25°,∠2=15°,则∠ABC=°;猜想:此时数量关系是:∠ABC= , 请说明理由;(2)、如图②,当点B在点D的上方运动(A,B,C三点不在同一直线上)时,猜想:此时数量关系是:∠ABC= , 请说明理由;(3)、如图③,当点B在点E的下方运动(A,B,C三点不在同一直线上)时,猜想:此时数量关系是:∠ABC=.19. 如图,已知AM//BN, ,点 是射线 上一动点(与点 不重合), 、 分别平分 和 ,分别交射线 于 、 .
(1)、如图①,当点B在线段DE上运动(点B不与D,E重合)时,若∠1=25°,∠2=15°,则∠ABC=°;猜想:此时数量关系是:∠ABC= , 请说明理由;(2)、如图②,当点B在点D的上方运动(A,B,C三点不在同一直线上)时,猜想:此时数量关系是:∠ABC= , 请说明理由;(3)、如图③,当点B在点E的下方运动(A,B,C三点不在同一直线上)时,猜想:此时数量关系是:∠ABC=.19. 如图,已知AM//BN, ,点 是射线 上一动点(与点 不重合), 、 分别平分 和 ,分别交射线 于 、 . (1)、求 的度数;(2)、在点P的运动过程中,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数是 , 并说明理由.20. 探究题
(1)、求 的度数;(2)、在点P的运动过程中,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数是 , 并说明理由.20. 探究题已知:如图1,AB∥CD,CD∥EF.求证:∠B+∠BDF+∠F=360°.
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究
 (1)、小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .(2)、接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线AB、EF,然后在平行线间画了一点 ,连接BD,DF后,用鼠标拖动点 ,分别得到了图2、图3、图4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和图4中的 、 与 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量和计算功能,找到了这三个角之间的数量关系.
(1)、小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .(2)、接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线AB、EF,然后在平行线间画了一点 ,连接BD,DF后,用鼠标拖动点 ,分别得到了图2、图3、图4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和图4中的 、 与 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量和计算功能,找到了这三个角之间的数量关系.请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图2中∠B、∠BDF与∠F之间的数量关系并加以证明;
②补全图4,直接写出∠B、∠BDF与∠F之间的数量关系: ▲ .
21. 如图,直线 , ,E、F在 上,且满足 , 平分(1)、求 的度数; (2)、若平行移动 ,那么 的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)、在平行移动 的过程中,是否存在某种情况,使 ?若存在,求出 度数;若不存在,说明理由.22. 已知 .
(2)、若平行移动 ,那么 的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)、在平行移动 的过程中,是否存在某种情况,使 ?若存在,求出 度数;若不存在,说明理由.22. 已知 .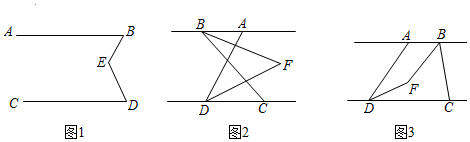 (1)、如图1, 为 , 之间一点,连接 , ,得到 .求证: ;(2)、如图,连接 , , 平分 , 平分 ,且 , 所在的直线交于点 .
(1)、如图1, 为 , 之间一点,连接 , ,得到 .求证: ;(2)、如图,连接 , , 平分 , 平分 ,且 , 所在的直线交于点 .①如图2,当点 在点 的左侧时,若 , ,求 的度数.
②如图3,当点 在点 的右侧时,设 , ,请你求出 的度数.(用含有 , 的式子表示)
23. 同学们以“一块直角三角板和一把直尺”开展数学活动,提出了很多数学问题,请你解答: (1)、如图1,∠α和∠β具有怎样的数量关系?请说明理由;(2)、如图2,∠DFC的平分线与∠EGC的平分线相交于点Q,求∠FQG的大小;(3)、如图3,点P是线段AD上的动点(不与A,D重合),连接PF、PG, 的值是否变化?如果不变,请求出比值;如果变化,请说明理由.24. 如图,已知直线 ,直线l与直线 、 分别交于点C和点D,点P是直线l上一动点,点A在直线 上,点B在直线 上,且点A和点B位于直线l同一侧.
(1)、如图1,∠α和∠β具有怎样的数量关系?请说明理由;(2)、如图2,∠DFC的平分线与∠EGC的平分线相交于点Q,求∠FQG的大小;(3)、如图3,点P是线段AD上的动点(不与A,D重合),连接PF、PG, 的值是否变化?如果不变,请求出比值;如果变化,请说明理由.24. 如图,已知直线 ,直线l与直线 、 分别交于点C和点D,点P是直线l上一动点,点A在直线 上,点B在直线 上,且点A和点B位于直线l同一侧.
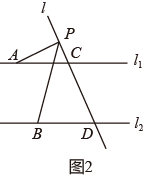
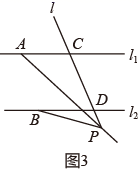 (1)、如图(1),当P点在线段CD(不含端点C和D)上运动时,求证: .(2)、如图(2),当点P运动到直线 上方时,试写出 、 和 三个角的数量关系,并证明.(3)、如图(3)当点P运动到直线 下方时,直接写出 、 和 三个角的数量关系.25. 如图,已知 , 是 的平分线.
(1)、如图(1),当P点在线段CD(不含端点C和D)上运动时,求证: .(2)、如图(2),当点P运动到直线 上方时,试写出 、 和 三个角的数量关系,并证明.(3)、如图(3)当点P运动到直线 下方时,直接写出 、 和 三个角的数量关系.25. 如图,已知 , 是 的平分线. (1)、若 平分 ,求 的度数;(2)、若 在 的内部,且 于 ,求证: 平分 ;(3)、在(2)的条件下,过点 作 ,分别交 、 于点 、 , 绕着 点旋转,但与 、 始终有交点,问: 的值是否发生变化?若不变,求其值;若变化,求其变化范围.
(1)、若 平分 ,求 的度数;(2)、若 在 的内部,且 于 ,求证: 平分 ;(3)、在(2)的条件下,过点 作 ,分别交 、 于点 、 , 绕着 点旋转,但与 、 始终有交点,问: 的值是否发生变化?若不变,求其值;若变化,求其变化范围.