2022年浙教版数学七下期中复习阶梯训练:平行线(优生加练)
试卷更新日期:2022-04-08 类型:复习试卷
一、单选题
-
1. 一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
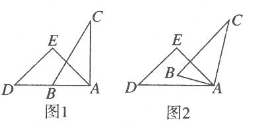 A、 和 B、 和 C、 和 D、以上都有可能2. 如右图,AB∥CD , PG平分∠EPF , ∠A+∠AHP=180°,下列结论:
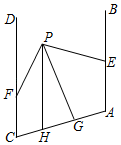
A、 和 B、 和 C、 和 D、以上都有可能2. 如右图,AB∥CD , PG平分∠EPF , ∠A+∠AHP=180°,下列结论:①CD∥PH;②∠BEP+∠DFP=2∠EPG;③∠FPH=∠GPH;④∠A+∠AGP+∠DFP﹣∠FPG=180°;⑤若∠BEP>∠DFP , 则 =2,
其中正确结论的个数是( )
 A、2个 B、3个 C、4个 D、5个3. 下列说法中正确的个数为( )
A、2个 B、3个 C、4个 D、5个3. 下列说法中正确的个数为( )①过一点有且只有一条直线与已知直线垂直;
②两条直线被第三条直线所截,同位角相等;
③经过两点有一条直线,并且只有一条直线;
④在同一平面内,不重合的两条直线不是平行就是相交.
A、1个 B、2个 C、3个 D、4个4. 如图,已知直线 、 被直线 所截, ,E是直线 右边任意一点(点E不在直线 , 上),设 , .下列各式:① ,② ,③ ,④ , 的度数可能是( ) A、①②③ B、①②④ C、①③④ D、①②③④5. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
A、①②③ B、①②④ C、①③④ D、①②③④5. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式: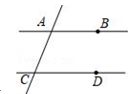
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A、①②③ B、①②④ C、①③④ D、①②③④ 图46. 如图,∠AOC和∠BOC互补,∠AOB=α , OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON的度数( )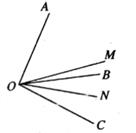 A、180°-2α B、 α C、90°+ α D、90°- α7. 如图,已知直线 , 被直线 所截, ,E是平面内任意一点(点E不在直线 , , 上),设 , .下列各式:① ,② ,③ ,④ , 的度数可能是( )
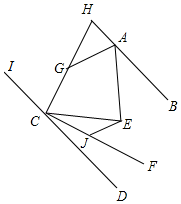
A、180°-2α B、 α C、90°+ α D、90°- α7. 如图,已知直线 , 被直线 所截, ,E是平面内任意一点(点E不在直线 , , 上),设 , .下列各式:① ,② ,③ ,④ , 的度数可能是( ) A、①②③ B、①②④ C、①③④ D、①②③④8. 如图,AB∥CD , CF平分∠ECD , HC⊥CF交直线AB于H , AG平分∠HAE交HC于G , EJ∥AG交CF于J , ∠AEC=80°,则下列结论正确的有( )个.
A、①②③ B、①②④ C、①③④ D、①②③④8. 如图,AB∥CD , CF平分∠ECD , HC⊥CF交直线AB于H , AG平分∠HAE交HC于G , EJ∥AG交CF于J , ∠AEC=80°,则下列结论正确的有( )个.①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.
 A、1 B、2 C、3 D、49. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A、1 B、2 C、3 D、49. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )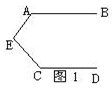


 A、、1个 B、2个 C、3个 D、4个10. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )
A、、1个 B、2个 C、3个 D、4个10. 如图,AB∥CD,点E为AB上方一点,FB,HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150°,则∠EFG的度数为( )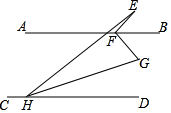 A、90° B、95° C、100° D、150°
A、90° B、95° C、100° D、150°二、填空题
-
11. 已知∠ABG为锐角,AH∥BG,点C从点B(点C不与点B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为点F(点F不与点A重合).若∠ECF=n°,则∠BAF=.(用n来表示)12. 如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是.13. 如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 . (填序号)
 14. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .
14. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .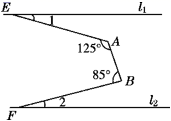 15. 平面直角坐标系中,点A(﹣5,3),B(0,3),C(﹣5,0),在y轴左侧一点P(a,b)(b≠0且点P不在直线AB上).若∠APO=40°,∠BAP与∠COP的角平分线所在直线交于D点,则∠ADO的度数为°.16. 已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED=°.
15. 平面直角坐标系中,点A(﹣5,3),B(0,3),C(﹣5,0),在y轴左侧一点P(a,b)(b≠0且点P不在直线AB上).若∠APO=40°,∠BAP与∠COP的角平分线所在直线交于D点,则∠ADO的度数为°.16. 已知如图,AB∥CD,∠A=130°,∠D=25°,那么∠AED=°.
三、解答题
-
17. 如图,在折线中,已知 , 延长、交于点 , 猜想与的关系,并说明理由.
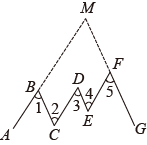 18. 如图已知AB//CD,试探究∠A,∠APC,∠C的数量关系.
18. 如图已知AB//CD,试探究∠A,∠APC,∠C的数量关系.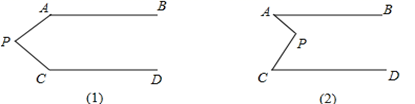 19. 如图,AB∥CD , 分别探讨下面四个图形中∠APC与∠A , ∠C的关系,请你从所得的关系中任意选取一个加以说明.
19. 如图,AB∥CD , 分别探讨下面四个图形中∠APC与∠A , ∠C的关系,请你从所得的关系中任意选取一个加以说明. (1)、图(1)结论:;图(2)结论:;图(3)结论:;图(4)结论: .(2)、你准备证明的是图 , 请在下面写出证明过程.20. 如图,在△ABC中,点E、H在BC上,EF⊥AB,HD⊥AB,垂足分别是F、D,点G在AC上,∠AGD=∠ACB,试说明∠1+∠2=180°.
(1)、图(1)结论:;图(2)结论:;图(3)结论:;图(4)结论: .(2)、你准备证明的是图 , 请在下面写出证明过程.20. 如图,在△ABC中,点E、H在BC上,EF⊥AB,HD⊥AB,垂足分别是F、D,点G在AC上,∠AGD=∠ACB,试说明∠1+∠2=180°.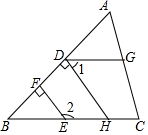 21. 如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
21. 如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.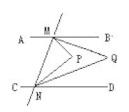 22. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,求∠DOF的度数.
22. 如图,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,求∠DOF的度数.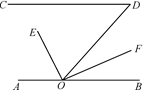
四、综合题
-
23. 如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
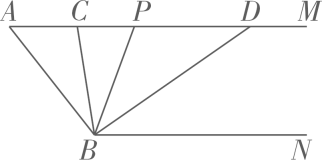 (1)、求∠CBD的度数;(2)、当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.24. 在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
(1)、求∠CBD的度数;(2)、当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.24. 在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.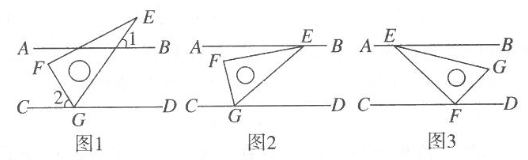 (1)、如图1,若三角尺的 角的顶点 放在CD上,若 ,求 的度数;(2)、如图2,小颓把三角尺的两个锐角的顶点E,G分别放在AB和CD上,请你探索并说明 与 间的数量关系;(3)、如图3,小亮把三角尺的直角顶点 放在CD上, 角的顶点 落在AB上.若 ,则 与 的数量关系是什么?用含 的式子表示并说明理由.25. 如图①.已知 , 点B为平面内一点,于点B,过点B作于点D,设.
(1)、如图1,若三角尺的 角的顶点 放在CD上,若 ,求 的度数;(2)、如图2,小颓把三角尺的两个锐角的顶点E,G分别放在AB和CD上,请你探索并说明 与 间的数量关系;(3)、如图3,小亮把三角尺的直角顶点 放在CD上, 角的顶点 落在AB上.若 ,则 与 的数量关系是什么?用含 的式子表示并说明理由.25. 如图①.已知 , 点B为平面内一点,于点B,过点B作于点D,设.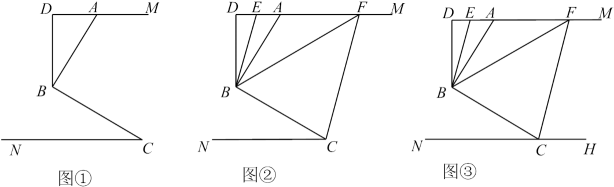 (1)、若 , 求的度数;(2)、如图②,若点E、F在上,连接、、 , 使得平分、平分 , 求的度数;(3)、如图③,在(2)问的条件下,若平分 , 且 , 求的度数.
(1)、若 , 求的度数;(2)、如图②,若点E、F在上,连接、、 , 使得平分、平分 , 求的度数;(3)、如图③,在(2)问的条件下,若平分 , 且 , 求的度数.