2022年浙教版数学七下期中复习阶梯训练:平行线(提高训练)
试卷更新日期:2022-04-08 类型:复习试卷
一、单选题
-
1. 如图l1∥l2点О在直线l1上,将三角板的直角顶点放在点О处,三角板的两条直角边与l2交于A,B两点,若∠1=35°,则∠2的度数为( )
 A、35° B、45° C、55° D、65°2. 如果 与 的两边分别平行, 比 的4倍少 ,那么 的度数是( )A、10° B、 C、 或 D、以上都不对3. 如图,AB//DE,∠1=∠2,则AE与DC的位置关系是( )
A、35° B、45° C、55° D、65°2. 如果 与 的两边分别平行, 比 的4倍少 ,那么 的度数是( )A、10° B、 C、 或 D、以上都不对3. 如图,AB//DE,∠1=∠2,则AE与DC的位置关系是( ) A、相交 B、平行 C、垂直 D、无法确定4. 如图,下列角中属于同位角的是( )
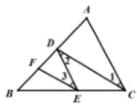
A、相交 B、平行 C、垂直 D、无法确定4. 如图,下列角中属于同位角的是( )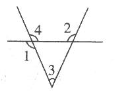 A、 与 B、 与 C、 与 D、 与5. 如图,在三角形ABC中,D,E,F分别为AB,AC,BC边上的点,且 ,那么下列结论中不正确的是( )
A、 与 B、 与 C、 与 D、 与5. 如图,在三角形ABC中,D,E,F分别为AB,AC,BC边上的点,且 ,那么下列结论中不正确的是( ) A、 B、 C、 D、6. 两直线被第三直线所截,则( )A、同位角相等 B、内错角相等 C、同旁内角互补 D、以上说法都不对7. 如图,如果 ∥ ,那么 , , 之间的关系为( )
A、 B、 C、 D、6. 两直线被第三直线所截,则( )A、同位角相等 B、内错角相等 C、同旁内角互补 D、以上说法都不对7. 如图,如果 ∥ ,那么 , , 之间的关系为( ) A、 B、 C、 D、8. 如图,已知直线 , 直线c被直线a、b所截,若 , 则( )
A、 B、 C、 D、8. 如图,已知直线 , 直线c被直线a、b所截,若 , 则( ) A、62° B、28° C、128° D、118°9. 如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定 的个数是( )
A、62° B、28° C、128° D、118°9. 如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定 的个数是( )① ;② ;③ ;④ .
 A、1 B、2 C、3 D、410. 如图所示,由 可得出( )
A、1 B、2 C、3 D、410. 如图所示,由 可得出( ) A、 (两直线平行,内错角相等) B、 内错烉相等,两直线平行) C、 (内错黎相等,两直线平行) D、 (两直线平行,内锆角相等)
A、 (两直线平行,内错角相等) B、 内错烉相等,两直线平行) C、 (内错黎相等,两直线平行) D、 (两直线平行,内锆角相等)二、填空题
-
11. 如图,将直角三角板 与直尺贴在一起,使三角板 的直角顶点 在直尺的一边上,若 ,则 的度数为.
 12. 如图,在不添加辅助线及字母的前提下,请写出一个能判定 的条件:.
12. 如图,在不添加辅助线及字母的前提下,请写出一个能判定 的条件:. 13. 如图,点B,C,D在同一条直线上, ,如果 ,那么 .
13. 如图,点B,C,D在同一条直线上, ,如果 ,那么 . 14. 如图, 平分 ,直尺与OC垂直,则 .
14. 如图, 平分 ,直尺与OC垂直,则 . 15. 纸带沿AB折叠的三种方法如图所示,有以下结论:①如图1,展开后测得∠1=∠2;②如图2,展开后测得∠1=∠2且∠3=∠4;③如图3,测得∠1=∠2.其中能判定纸带两条边a,b互相平行的是.(填序号).
15. 纸带沿AB折叠的三种方法如图所示,有以下结论:①如图1,展开后测得∠1=∠2;②如图2,展开后测得∠1=∠2且∠3=∠4;③如图3,测得∠1=∠2.其中能判定纸带两条边a,b互相平行的是.(填序号). 16. 如图所示, 和 互余,则 .
16. 如图所示, 和 互余,则 .
三、解答题
-
17. 如图,CA是∠BCD的平分线﹐∠A=30°,∠BCD=60°,求证:AB∥CD.
 18. 如图,已知∠1=∠2 求证:a∥b.
18. 如图,已知∠1=∠2 求证:a∥b. 19. 已知,如图,CD平分∠ACB, ,∠AED=82°.求∠EDC的度数.下面是小明同学的证明过程,请在括号内填上恰当的依据.
19. 已知,如图,CD平分∠ACB, ,∠AED=82°.求∠EDC的度数.下面是小明同学的证明过程,请在括号内填上恰当的依据.
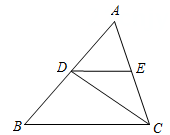
证明: (已知)
∴∠ACB=∠AED( )
∠EDC=∠DCB( )
又∵CD平分∠ACB(已知)
∴ ( )
又∵∠AED=82°(已知)
∴∠ACB=82°( )
∴ ,
∴∠EDC=∠DCB=41°( )
20. 如图,已知AB∥CD,∠A=60°,∠ECD=120°,求∠ECA的度数. 21. 已知,如图,∠ACB=60°,∠ABC=50°,BO、CO分别平分∠ABC、∠ACB,EF是经过点O且平行于BC的直线,求∠BOC的度数.
21. 已知,如图,∠ACB=60°,∠ABC=50°,BO、CO分别平分∠ABC、∠ACB,EF是经过点O且平行于BC的直线,求∠BOC的度数. 22. 已知:如图, , .
22. 已知:如图, , .求证: ∥ .

四、综合题