2022年江苏省镇江市中考数学模拟卷1
试卷更新日期:2022-04-08 类型:中考模拟
一、填空题(每题2分,共24分)
-
1. 某有理数满足它的绝对值等于它的相反数,写出一个符合该条件的数 .2. 使有意义的x的取值范围是.3. 若8的平方根和立方根分别是 和 ,则 .4. 如图,正八边形的两条对角线AC、BE相交于点P,∠CPE的度数为.
 5. 已知(x+3)(x﹣2)+m=x2+x,则一元二次方程x2+x﹣m=0的根是 .6. 中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如下表:
5. 已知(x+3)(x﹣2)+m=x2+x,则一元二次方程x2+x﹣m=0的根是 .6. 中药是以我国传统医药理论为指导,经过采集、炮制、制剂而得到的药物.在一个时间段,某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如下表:中药
黄芪
焦山楂
当归
销售单价(单位:元/千克)
80
60
90
销售额(单位:元)
120
120
360
则在这个时间段,该中药房的这三种中药的平均销售量为千克.
7. 从-1, ,2中任取两个不同的数作积,则所得积的中位数是.8. △ABC中,AB=8,AC=6,点D在AC上且AD=2,如果要在AB上找一点E,使△ADE与原三角形相似,那么AE=9. 如图,正方形ABCD和正方形AEFG的边长分别为5 cm和3 cm,点E、G分别为AB、AD边上的点,H为CF的中点,连接HG,则HG的长为cm.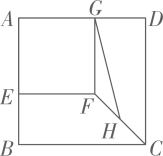 10. 已知一次函数 ,当 时,y的最大值是 .11. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的编号为1~7的小正方形中任意一个涂黑,则所得图案是一个轴对称图形的概率是.
10. 已知一次函数 ,当 时,y的最大值是 .11. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的编号为1~7的小正方形中任意一个涂黑,则所得图案是一个轴对称图形的概率是.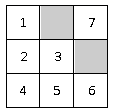 12. 如图,已知Rt△ABC中,∠ABC=90°,∠ACB=30°,斜边AC=4,点P是三角形内的一动点,则PA+PB+PC的最小值是 .
12. 如图,已知Rt△ABC中,∠ABC=90°,∠ACB=30°,斜边AC=4,点P是三角形内的一动点,则PA+PB+PC的最小值是 .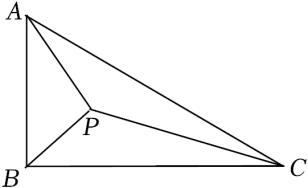
二、单选题(每题3分,共18分)
-
13. 如图所示的几何体的左视图是( )
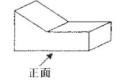 A、
A、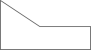 B、
B、 C、
C、 D、
D、 14. 海南的富铁矿是国内少有富铁矿之一,储量居全国第6位,其储量约为237 000 000吨,用科学记数法表示应为( )A、237×106吨 B、2.37×107吨 C、2.37×108吨 D、0.237×108吨15. 如图, 、 是 的切线, 、 为切点,点 在 上,且 ,则 的度数为( )
14. 海南的富铁矿是国内少有富铁矿之一,储量居全国第6位,其储量约为237 000 000吨,用科学记数法表示应为( )A、237×106吨 B、2.37×107吨 C、2.37×108吨 D、0.237×108吨15. 如图, 、 是 的切线, 、 为切点,点 在 上,且 ,则 的度数为( )
 A、55° B、65° C、70° D、90°16. 某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )A、800元 B、600元 C、1200元 D、1000元17. 如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AD的长为( )
A、55° B、65° C、70° D、90°16. 某商场降价销售一批名牌球鞋,已知所获利润y(元)与降价金额x(元)之间满定函数关系式y=﹣x2+50x+600,若降价10元,则获利为( )A、800元 B、600元 C、1200元 D、1000元17. 如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AD的长为( ) A、8cm B、7cm C、6cm D、5cm18. 将数按以下规律排列:1,2,3,2,5,2,7,2,9,2,11……,以此类推,四个同学分别得出一个结论:
A、8cm B、7cm C、6cm D、5cm18. 将数按以下规律排列:1,2,3,2,5,2,7,2,9,2,11……,以此类推,四个同学分别得出一个结论:杨一:第99个数是99;
张三:第2022个数是2;
李四:前101个数的和为2652;
王五,前200个数中有7个完全平方数;
四个结论正确的有( )个
A、4 B、3 C、2 D、1三、解答题
-
19. 计算:(1)、(2)、20.(1)、计算:(2)、解不等式组21. 一个不透明的口袋中有4个大小,质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.22. 如图,四边形 是平行四边形.
 (1)、尺规作图(不写作法,保留作图痕迹);作出 的角平分线 ,交 于点 ;在线段 上截取 ,连接 ;(2)、在(1)所作图中,请判断四边形 的形状,并说明理由.23. 《九章算术》中有这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?其大意如下:今有5只雀、6只燕,分别放一起用衡器称,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置放,两边重量相等.5只雀、6只燕重量为1斤(注:声代1斤=16两).问每只雀、燕各重多少两?24. 为培养学生良好的运动习惯和运动能力,我校本学期开展了“趣味运动会”和“冬季长跑”等体育活动.为了解九年级学生的长跑水平,我校对全体九年级同学进行了长跑测试,体育组陈老师随机抽取20名男生和20名女生的测试成绩(满分100)进行整理和分析(成绩共分成五组:A. ,B. ,C. ,D. ,E. ),绘制了不完整的统计图表:
(1)、尺规作图(不写作法,保留作图痕迹);作出 的角平分线 ,交 于点 ;在线段 上截取 ,连接 ;(2)、在(1)所作图中,请判断四边形 的形状,并说明理由.23. 《九章算术》中有这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?其大意如下:今有5只雀、6只燕,分别放一起用衡器称,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置放,两边重量相等.5只雀、6只燕重量为1斤(注:声代1斤=16两).问每只雀、燕各重多少两?24. 为培养学生良好的运动习惯和运动能力,我校本学期开展了“趣味运动会”和“冬季长跑”等体育活动.为了解九年级学生的长跑水平,我校对全体九年级同学进行了长跑测试,体育组陈老师随机抽取20名男生和20名女生的测试成绩(满分100)进行整理和分析(成绩共分成五组:A. ,B. ,C. ,D. ,E. ),绘制了不完整的统计图表:
收集、整理数据20名男生的长跑成绩分别为:
76,77,95,88,50,89,89,97,99,93,97,89,65,87,68,89,78,88,98,88.
女生长跑成绩在C组和D组的分别为:
73,74,74.74,74,76,83,88,89.


分析数据:两组样本数据的平均数、中位数和众数如表所示:长跑成绩
平均数
中位数
众数
男生
85
88.5
b
女生
81.8
a
74
请根据以上信息,回答下列问题;
(1)、①补全频数分布直方图;②填空:a= ▲ , ▲ ;
(2)、根据以上数据,你认为九年级学生是男生的长跑的成绩更好还是女生的长跑成绩更好?判断并说明理由(一条理由即可);(3)、如果我校九年级有男生900名,女生600名,请估计九年级长跑成绩不低于80分的学生人数.25. 已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=的图象的两个交点; (1)、求此反比例函数和一次函数的解析式;(2)、根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;(3)、求△AOB的面积.26. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接AD,过点D作DM⊥AC,垂足为M,AB、MD的延长线交于点N.
(1)、求此反比例函数和一次函数的解析式;(2)、根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;(3)、求△AOB的面积.26. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连接AD,过点D作DM⊥AC,垂足为M,AB、MD的延长线交于点N. (1)、求证:MN是⊙O的切线;(2)、求证:DN2=BN•(BN+AC);(3)、若BC=6,cosC= ,求DN的长.27. 如图,已知;抛物线y= x2+bx+c经过点A(0,2),点C(4,0),且交x轴于另一点B.
(1)、求证:MN是⊙O的切线;(2)、求证:DN2=BN•(BN+AC);(3)、若BC=6,cosC= ,求DN的长.27. 如图,已知;抛物线y= x2+bx+c经过点A(0,2),点C(4,0),且交x轴于另一点B.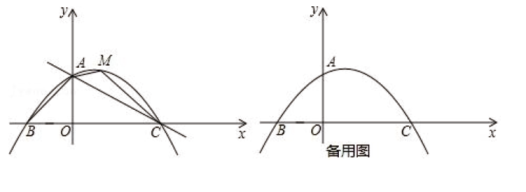 (1)、求抛物线的解析式;(2)、在直线AC上方的抛物线上有一点M,求三角形ACM面积的最大值及此时点M的坐标;(3)、将线段OA绕x轴上的动点P(m,0)顺时针旋转90°得到线段O'A',若线段O'A’与抛物线只有一个公共点,请结合函数图象,求m的取值范围.28. 如图
(1)、求抛物线的解析式;(2)、在直线AC上方的抛物线上有一点M,求三角形ACM面积的最大值及此时点M的坐标;(3)、将线段OA绕x轴上的动点P(m,0)顺时针旋转90°得到线段O'A',若线段O'A’与抛物线只有一个公共点,请结合函数图象,求m的取值范围.28. 如图 (1)、如图①,点A、点B在直线 同侧,请你在直线 上找一点P,使得AP+BP的值最小;(不需要说明理由)(2)、如图②, ,点P为∠AOB内一定点, ,点E,F分别在OA,OB上,△PEF的周长是否存在最小值?若存在,请求出最小值,若不存在,请说明理由:(3)、如图③,已知四边形OABC中, , , , ,点H为OA边上的点,且OH=4,点P,F分别在AB,OC上运动,点E在线段OH上运动,连接EF,EP,PF,△EFP的周长是否存在最小值?若存在,请求出△EFP周长最小值和此时OE的长,若不存在,请说明理由.
(1)、如图①,点A、点B在直线 同侧,请你在直线 上找一点P,使得AP+BP的值最小;(不需要说明理由)(2)、如图②, ,点P为∠AOB内一定点, ,点E,F分别在OA,OB上,△PEF的周长是否存在最小值?若存在,请求出最小值,若不存在,请说明理由:(3)、如图③,已知四边形OABC中, , , , ,点H为OA边上的点,且OH=4,点P,F分别在AB,OC上运动,点E在线段OH上运动,连接EF,EP,PF,△EFP的周长是否存在最小值?若存在,请求出△EFP周长最小值和此时OE的长,若不存在,请说明理由.