2022年浙教版数学八下期中复习阶梯训练：数据分析初步（优生集训）
试卷更新日期：2022-04-07 类型：复习试卷
一、综合题
-
1. 某同学参加了学校举行的“五好小公民·红旗飘飘”演讲比赛，7名评委给该同学的打分(单位：分)情况如下表：
评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
(1)、直接写出该同学所得分数的众数与中位数.(2)、计算该同学所得分数的平均数.2. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩，测试规则为连续接球10个，每垫球到位1个记1分.
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩（分）
7
6
8
7
7
5
8
7
8
7
(1)、小明将三人的成绩整理后制作了下面的表格：平均数
中位数
众数
方差
甲
7
b
7
0.8
乙
7
7
d
0.4
丙
a
c
e
0.81
则表中a= ， b= ， c= ， d= ， e=.
(2)、若在他们三人中选择一名垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？请作出简要分析.3. 某中学九年级学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩（单位：个）1号
2号
3号
4号
5号
总数
甲班
100
98
110
89
103
500
乙班
90
97
101
113
99
500
经统计发现两班5名学生踢毽子的总个数相等，此时有学生建议，可以通过考查数据中的其他信息为参考，请你回答下列问题：
(1)、甲班比赛数据的中位数为 ，乙班比赛数据的平均数为；(2)、计算两班比赛数据的方差；(3)、根据以上信息，你认为应该把冠军奖状发给哪一个班？简述理由.4. “双减”政策实施以来，我校积极探寻更为合理的学生评价方案.班主任石老师对班级学生的学习生活等采取的是量化积分制.下面统计的是博学组和笃行组连续八周的量化积分，并将得到的数据制成如下的统计表：量化积分统计表（单位：分）
周次
组别
一
二
三
四
五
六
七
八
博学组
12
14
16
14
14
13
15
14
笃行组
13
11
15
17
16
18
13
9
(1)、请根据表中的数据完成下表平均数
中位数
众数
方差
博学组
14
14
笃行组
14
8.25
(2)、根据量化积分统计表中的数据，请在下图中画出笃行组量化积分的折线统计图.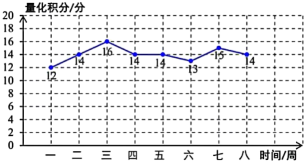
(3)、根据折线统计图中的信息，请你对这两个小组连续八周的学习生活情况作出一条简要评价.5. 在“心系灾区”自愿捐款活动中，某班30名同学的捐款情况如下表：捐款（元）
5
10
15
20
25
30
人数
11
9
6
2
1
1
(1)、这个班级捐款总数是多少元？(2)、求这30名同学捐款的平均数。6. 某校欲招聘一名数学教师，学校对甲、乙、丙三位候选人进行了三项能力测试，各项测试成绩满分均为100分，根据结果择优录用。三位候选人的各项测试成绩如下表所示（单位：分）：测试项目
测试成绩
甲
乙
丙
教学能力
85
73
73
科研能力
70
71
65
组织能力
64
72
84
(1)、如果根据三项测试的平均成绩，谁将被录用？请说明理由；(2)、根据实际需要，学校将教学、科研和组织三项能力测试的得分按5：3：2的比例来确定每人的成绩，谁将被录用？请说明理由。7. 一次期中考试中，A，B，C，D，E五位同学的数学、英语成绩有如下信息：A
B
C
D
E
平均分
方差
数学
71
72
69
68
70
____
2
英语
88
82
94
85
76
85
____
(1)、求这五位同学在本次考试中数学成绩的平均分和英语成绩的方差；(2)、为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分=从标准分看，标准分大的考试成绩更好，请问A同学在本次考试中，数学与英语哪个学科考得更好？
8. 为了给车间18名工人确定生产任务，某厂对上月生产情况进行了统计，结果如下表所示：产量（件）
40
30
10
9
8
人数
1
1
5
8
3
(1)、计算他们月产量的平均数、众数及中位数；(2)、以月平均数作为月生产任务合理吗？为什么？你认为把月生产任务定为多少比较合理？
9. 下表是某校八年级（1）班20名学生某次数学测验的成绩统计表：成绩（分）
60
70
80
90
100
人数
1
5
x
x
2
(1)、若这20名学生成绩的平均数为82分，求x和y的值。(2)、在（1）的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值。10. 某校举办弘扬中华传统知识演讲比赛，八（1）班计划从甲、乙两位同学中选出一位参加学校的决赛，已知这两位同学在预赛中各项成绩如表图：
(1)、表中a的值为；b的值为 ．(2)、把图中的统计图补充完整；(3)、若演讲内容、语言表达、形象风度、现场效果四项得分按30%、50%、10%、10%的权重比例计算两人的最终得分，并选择最终得分较高的同学作为代表参赛，那么谁将代表八（1）班参赛?请说明理由．项目
甲的成绩（分）
乙的成绩（分）
演讲内容
95
90
语言表达
90
85
形象风度
85
b
现场效果
90
95
平均分
a
90
11. 甲、乙两校参加区举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，统计学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图和统计表：甲校成绩统计表
成绩
7分
8分
9分
10分
人数
11
0
x
8
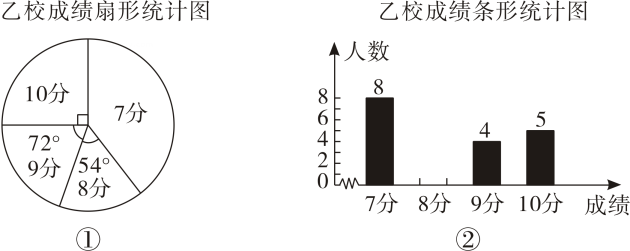(1)、甲校参赛人数是人，；(2)、请你将如图②所示的统计图补充完整；(3)、请分别求出甲校和乙校学生成绩的平均数和中位数，并从平均数和中位数的角度分析哪个学校的成绩较好？12. 为了解某校八年级体育科目训练情况，从八年级学生中随机抽取了部分学生进行了一次体育科目测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图请根据统计图中的信息解答下列问题：
(1)、图1中的度数是 ▲ ， 并把图2条形统计图补充完整．(2)、抽取的这部分的学生的体育科目测试结果的中位数是在级；(3)、依次将优秀、良好、及格、不及格记为90分、80分、70分、50分，请计算抽取的这部分学生体育的平均成绩．13. 某县教育局组织了一次经典诵读比赛，中学组有两队各10人的比赛成绩如下表：甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)、甲队成绩的中位数是分，乙队成绩的众数是分；(2)、计算乙队的平均成绩；(3)、如果要从两个队中选择一对参加市级比赛，你认为安排哪个队更容易获奖．14. 为响应“双减”政策，老师们都精心设计每天的作业，兴华学校调查了部分学生每天完成作业所用时间，并用得到的数据绘制了如下不完整的统计图，根据图中信息完成下列问题：
(1)、将条形统计图补充完整；(2)、抽查学生完成作业所用时间的众数是；(3)、求所有被抽查学生完成作业所用的平均时间．15. 某校开展了以“不忘初心，奋斗新时代”为主题的读书活动，校德育处对本校八年级学生九月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了抽样调查，随机抽取八年级部分学生，对他们的“读书量”（单位：本）进行了统计，并将统计结果绘制成了如下统计图：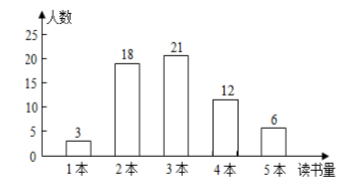
(1)、本次所抽取学生九月份“读书量”的众数为本，中位数为本；(2)、求本次所抽取学生九月份“读书量”的平均数.16. 体育课上，七年级某班男同学进行了100米测验，达标成绩为15秒，下表是梦想小组8名男生的成绩记录，其中“+”表示成绩大于15秒.﹣0.8
+1
﹣1.2
0
﹣0.7
+0.6
﹣0.4
﹣0.1
问：
(1)、这个小组男生的达标率为多少？（达标率＝）(2)、这个小组男生的平均成绩是多少秒？17. 甲、乙两人在相同的情况下各打靶6次，每次打靶的成绩依次如下（单位：环）：甲：10，7，8，7，8，8
乙：5，6，10，8，9，10
(1)、甲成绩的众数 ， 乙成绩的中位数.(2)、计算乙成绩的平均数和方差；(3)、已知甲成绩的方差是1环，则的射击成绩离散程度较小.（填“甲”或“乙”）18. 甲、乙、丙三名候选人要参加学校学生会干部竞选，按程序分别进行答辩、笔试和民主投票.答辩、笔试成绩如下表所示，学生民主投票每张选票只限填写甲、乙、丙中的一人，且每张选票记1分.统计得票后，绘出如下所示不完整的统计图.答辩、笔试成绩统计表
人员
甲
乙
丙
答辩成绩（分）
95
88
86
笔试成绩（分）
80
86
90
根据以上信息，请解答下列问题.
(1)、参加投票的共有人，乙的得票率是.(2)、补全条形统计图.(3)、学校将答辩、笔试和学生投票三项得分按4：4：2的比例确定每位候选人的总成绩，总成绩最高者当选，试通过计算说明哪位候选人当选.19. 2021年是中国共产党建党100周年，某校开展了全校教师学习党史活动并进行了党史知识竞赛，从七、八年级中各随机抽取了20名教师，统计这部分教师的竞赛成绩（竞赛成绩均为整数，满分为10分，9分及以上为优秀）．相关数据统计、整理如下：抽取七年级教师的竞赛成绩（单位：分）
6，7，7，8，8，8，8，8，8，8，8，9，9，9，9，10，10，10，10，10．
八年级教师竞赛成绩扇形统计图
七，八年级教师竞赛成绩统计表年级
七年级
八年级
平均数
8.5
8.5
中位数
9
众数
8
优秀率
45%
55%
根据以上信息，解答下列问题：
(1)、填空： ， ；(2)、估计该校七年级120名教师中竞赛成绩达到8分及以上的人数；(3)、根据以上数据分析，从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异．20. 某学校从九年级同学中任意选取40人，随机分成甲、乙两个小组进行“引体向上”体能测试，根据测试成绩绘制出统计表和如图所示的统计图（成绩均为整数，满分为10分）甲组成绩统计表：
成绩
7
8
9
10
人数
1
9
5
5
乙组成绩统计图
根据上面的信息，解答下列问题：
(1)、甲组的平均成绩为分， ， 甲组成绩的中位数是 ， 乙组成绩的众数是；(2)、若已经计算出甲组成绩方差为0.81，求出乙组成绩的方差，并判断哪个小组的成绩更加稳定？21. 某校春季运动会计划从七年级三个班中评选一个精神文明队，评比内容包括：“开幕式得分”，“纪律卫生”和“投稿及播稿情况”三项（得分均为整数分），三个班的各项得分（不完整）如图所示．
(1)、“开幕式”三个班得分的中位数是；“纪律卫生”三个班得分的众数是；(2)、根据大会组委会的规定：“开幕式”，“纪律卫生”，“投稿及播稿情况”三项按4：4：2的比例确定总成绩，总成绩高的当选精神文明队，已知七年级一班的总成绩为79分．①请计算七年级二班的总成绩；
②若七年级三班当选精神文明队，请求出七年级三班在“投稿及播稿情况”方面的最少得分？
22. 某中学为选拔一名选手参加我市“学宪法 讲宪法”主题演讲比赛，经研究，按表所示的项目和权数对选拔赛参赛选手进行考评．下图分别是是小明、小华在选拔赛中的得分表和各项权数分布表：得分表
项目
选手
服装
普通话
主题
演讲技巧
小明
85分
70分
80分
85分
小华
90分
75分
75分
80分
结合以上信息，回答下列问题：
(1)、小明在选拔赛中四个项目所得分数的众数是 ， 中位数是；(2)、评分时按统计表中各项权数考评．①求出演讲技巧项目对应扇形的圆心角的大小．
②如此考评，小明和小华谁更优秀，派出哪位同学代表学校参加比赛呢？
23. 为了解某校九年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：
(1)、求出本次抽测的男生人数及图①中m的值，并补全图②；(2)、写出本次抽测成绩的众数、中位数；(3)、若规定引体向上5次以上（含5次）为体能达标，根据样本数据，估计该校350名九年级男生中有多少人体能达标．24. 表格是小明一学期数学成绩的记录，根据表格提供的信息回答下面的问题．考试类别
平时
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩
88
92
90
86
90
96
(1)、小明6次成绩的众数是分；中位数是分；(2)、计算小明平时成绩的平均分；(3)、计算小明平时成绩的方差；(4)、按照学校规定，本学期的综合成绩的权重如图所示，请你求出小明本学期的综合成绩，要写出解题过程．（注意：①平时成绩用四次成绩的平均数；②每次考试满分都是100分）．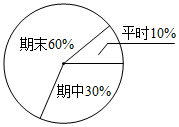
25. 某初中学校积极实施综合素质评定。从"道德品质"、"公民素养"、学习能力"、"交流合作"、"运动与健康"、审美与表现"六个维度进行量化考核(每项满分120分)。某学生本学期6项考核成绩如下表所示：
成绩类别
道德品质
公民素养
交流合作
学习能力
运动健康
审美表现
成绩/分
112
105
110
108
113
108
(1)、6项考核成绩的中位数为 ， 众数为(2)、求该生6项考核成绩的平均成绩．(3)、如果本学期的总评成绩按照"公民素养"、"咬流合作"、"运动与健康"、"审美与表现"成绩各占10%，学习能力"成绩占20%，"道德品质"成绩占40%计算，那么该生本学期的综合评定成绩是多少？