安徽省合肥市瑶海区2022年中考一模数学试题

试卷更新日期：2022-04-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 在（－1）²、－1、0、－ $\frac{3}{2}$ 中，四个数中，最大的数是（）

A、（－1）² B、－1 C、0 D、－ $\frac{3}{2}$

查看试题解析
2. 下列运算结果为a⁵的是（）

A、a³＋a² B、
（a²）³
C、a¹⁰÷a² D、a²•a³

查看试题解析
3. 保护知识产权是鼓励创新的重要保障，据国家专利局统计： 2021 年我国共查处1500万件知识产权案件，有力打击了查版行为．数据1500万用科学记数法表示正确的是（）

A、15×10 B、15×10 C、15×10 D、15×10

查看试题解析
4. 如图是某个几何体的三视围，该几何体是（）

A、长方体 B、三棱柱 C、正方体 D、三棱锥

查看试题解析
5. 点O、A、B、C、D在数轴上的位置如图所示，O为原点，OA＝OB、AC＝1，若点B所表示的数为 $\sqrt{34}$ ，则点D所表示的整数为（）

A、－7 B、－6 C、－5 D、－4

查看试题解析
6. 如图，AB、AC是⊙O的切线，B、C为切点，点D是优弧BC上一点，∠BDC＝70°，则∠A的度数是（）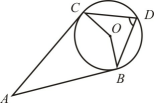

A、20° B、40° C、55° D、70°

查看试题解析
7. 中国正在布局以5G等为代表的战略性新兴产业，据统计2020年我国已建成5G基站a万座，计划2022年基站数量达到b万座，如果每年的平均增长率为x，则以下关系正确的是（）

A、a（1＋x）＝b B、b（1－x）＝a C、a（1＋2x）＝b D、a（1＋x）＝b

查看试题解析
8. 寒假期间，语文老师给学生布置了阅读任务，小国、小玲分别从《红楼梦》、《西游记》、《三国演义》三本名著中随机选择两本作为自己的阅读书目，则她俩选择的书目完全相同的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看试题解析
9. 实数x、y满足x²＋y²＝100，则xy的最大值是（）

A、25 B、50 C、24 D、48

查看试题解析
10. 在等边ΔABC中，AB＝4、AD是中线，点E是BD上点（不与B、D重合），点F是AC上一点，连接EF交AD于点G，CF＝2BE，以下结论不正确的是（）

A、当EF $/ /$ AB时，BE＝ $\frac{4}{3}$ B、当EF⊥AC时，CE＝4BE C、EG≠FG D、点G不可能是AD的中点

查看试题解析

二、填空题

11. 计算： $(- 2)^{0} - (\frac{1}{2})^{- 1}$ ＝

查看试题解析
12. 因式分解：ax-ax³=

查看试题解析
13. 如图，ΔABC中，AD是中线，点E在AD上，且CE＝CD＝1，∠BAD＝∠ACE，则AC的长为

查看试题解析
14. 二次函数y＝ax＋bx＋c（a≠0）的图象过点A（0，1）和C（－1，0）

(1)、若函数图象的对称轴是x＝－1，则函数解析式为

(2)、当a＝－2时，作直线x＝h（h＞0）交直线AC于P，交抛物线于点Q，交x轴于点D，当PQ＝QD时，h＝

查看试题解析
15. 如图是一种机器零件的示意图，其中AB⊥BE，CD⊥BE，测得AB＝5cm、CD＝3cm、∠CED＝45°，∠ACE＝175°，求零件外边缘ACE的长l＝（结果保留1位小数，参考数据： $\sqrt{2}$ ＝1.414，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

查看试题解析

三、解答题

16. 先化简、再求值： $\frac{2}{x^{2} - 4} \div \frac{1}{x^{2} - 2 x}$ ，其中x＝－ $\frac{1}{2}$ ．

查看试题解析
17. 如图，在平面直角坐标系中，ΔABC三个顶点的坐标分别为A（－3，－1），B （－4，－4），C（－1，－3）
⑴以O为旋转中心，将△ABC顺时针旋转90°得到△A₁B₁C₁；
⑵以O为对称中心，作出△ABC关于点O的中心对称图形ΔA₂B₂C₂；

查看试题解析
18. 在数学探究课上，老师布置如下活动：用若干个大小一样的小矩形拼成一个大矩形，探究图中包含的矩形（含正方形）个数，如图1，是由两个小矩形组成的一个图形，该图中共有3个矩形．尝试解决以下问题：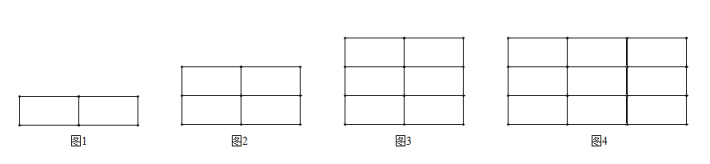

(1)、图2是由4个小矩形组成的图形，该图中共有个矩形；图3是由6个小矩形组成的图形，该图中共有个矩形；

(2)、小军在与同学探究时发现，矩形的个数与最大矩形的长和宽所包含的线段条数有关．如图4，最大矩形的长包含6条线段，宽也包含6条线段，则该图中共有个矩形；若某大矩形是由mn个矩形组成，则该图中共有个小矩形；（备注：1＋2＋3＋……＋n＝ $\frac{n (n + 1)}{2}$ ）

查看试题解析
19. 如图，直线y₁＝mx与双曲线y₂＝ $\frac{n}{x}$ 交于点A、B，过点A作AP⊥x轴，垂足点P的坐标是（－2，0），连接BP，且SΔABP＝2．

(1)、求反比例函数的解析式；

(2)、当y₁＞y₂时，求x的取值范围

查看试题解析
20. 已知：RtΔACB中， ∠C＝90°，以AC为直径的⊙O交AB于E，点F为弧EC的中点，OF的延长线交CB于D．

(1)、求证：CD＝BD；

(2)、连接EC交OD于G，若AC＝6、CD＝4，求GF的长．

查看试题解析
21. 北京冬奥会正式比赛项目冬季两项是融滑雪和射击于一体的项目，要求运动负滑行一段时间再进行射击，对运动员的体能和稳定性都是极大的考验．某冬季两项集训队为了解运动员滑雪后射击的准确性，从甲、乙两个队分别抽了40名运动员进行了模拟测试，并将他们滑雪10公里后的射击成绩进行了整理、描述和分析，下面给出了部分信息．（说明：成绩8.0～10环及以上为优秀；7.0～7.9环为良好；6.0～6.9环为合格；6.0 环以下为不合格）．
①甲队运动员成绩的频数分布直方图如下图所示（数据分为五组：5≤x＜6；6≤x＜7；7≤x＜8；8≤x＜9；9≤x≤10）
②甲队运动员射击成绩在7≤x＜8这一组的是：7、7.1、7.3，7.3、7.3、7.4、7.6、7.7、7.8、7.9；
③乙队运动员的成绩中没有3人相同，其平均数、中位数、众数、优秀率如下：
平均数
中位数
众数
优秀率
7.9
7.6
8.4
40%
根据以上信息，回答下列问题：

(1)、求甲队运动员射击成绩在7≤x＜8这组数据的中位数和众数；

(2)、成绩是7.6环的运动员，在哪个队里的名次更好些？请说明理由；

(3)、根据上述信息，推断队运动员滑雪后射击状态状况更好，理由为（至少从两个不同的角度说明推断的合理性）

查看试题解析
22. 已知：抛物线y＝－x²＋kx＋k＋1（k＞1）与x轴交于A、B两点，（点A在点B的左侧），与y轴交于点C．

(1)、k＝2时，求抛物线的顶点坐标；

(2)、若抛物线经过一个定点，求这个定点的坐标；

(3)、点P为抛物线上一点，且位于直线BC上方，过点P作PF∥y轴，交BC于点F，求PF长度的最大值（用含k式子表示）．

查看试题解析
23. 已知：矩形ABCD中，E为BC中点，AE⊥BD于F，AB＝2 $\sqrt{2}$

(1)、求证：DF＝2BF

(2)、求CF的长；

(3)、延长CF交AB于点H，将△BCF沿直线CH翻折为△B′FC，B′C交BD于点G，延长CB′交AD于点M，求 $\frac{A M}{M D}$ 的值．

查看试题解析

平均数	中位数	众数	优秀率
7.9	7.6	8.4	40%