安徽省C20教育联盟2022年九年级第一次学业水平检测数学试题
试卷更新日期:2022-04-07 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列运算中正确的是( )A、 B、 C、 D、3. 下列几何体中,其俯视图与主视图完全相同的是( )A、
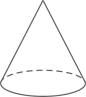 B、
B、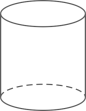 C、
C、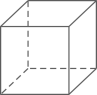 D、
D、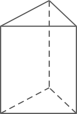 4. 2022年1月15日,国家卫健委新闻发言人在国务院联防联控机制新闻发布会上表示,要持续推进新冠病毒疫苗接种,截止14日,完成全程接种的人数为122058.4万人,其中数据122058.4万用科学记数法表示为( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 有长度分别为3cm,5cm,7cm,9cm的四条线段,从中任取三条线段能够组成三角形的概率是( )
4. 2022年1月15日,国家卫健委新闻发言人在国务院联防联控机制新闻发布会上表示,要持续推进新冠病毒疫苗接种,截止14日,完成全程接种的人数为122058.4万人,其中数据122058.4万用科学记数法表示为( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 有长度分别为3cm,5cm,7cm,9cm的四条线段,从中任取三条线段能够组成三角形的概率是( )
A、 B、 C、 D、7. 在“双减政策”的推动下,某校学生课后作业时长有了明显的减少.去年上半年平均每周作业时长为a分钟,经过去年下半年和今年上半年两次整改后,现在平均每周作业时长比去年上半年减少了70%,设每半年平均每周作业时长的下降率为x,则可列方程为( )A、 B、 C、 D、8. 如图,上有A、B两点,点C为弧AB上一点,点P是外一点,且 , , 则的度数为( )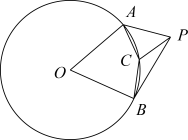 A、 B、 C、 D、9. 已知抛物线经过点 , 且当时, , 则下列判断正确的是( )A、 , B、 , C、 , D、 ,10. 如图,在和中, , , , 点M、N、P分别为EF、BC、CE的中点,若绕点A在平面内自由旋转,面积的最大值为( )
A、 B、 C、 D、9. 已知抛物线经过点 , 且当时, , 则下列判断正确的是( )A、 , B、 , C、 , D、 ,10. 如图,在和中, , , , 点M、N、P分别为EF、BC、CE的中点,若绕点A在平面内自由旋转,面积的最大值为( ) A、24 B、18 C、12 D、20
A、24 B、18 C、12 D、20二、填空题
-
11. 计算: .12. “同位角相等”的逆命题是 .
13. 反比例函数与在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则的面积为 .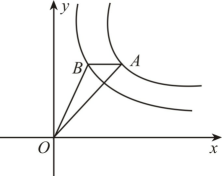 14. 在矩形ABCD中, , , E是BC的中点,连接AE,过点D作于点F,连接CF、AC.(1)、线段DF的长为;(2)、若AC交DF于点M,则 .
14. 在矩形ABCD中, , , E是BC的中点,连接AE,过点D作于点F,连接CF、AC.(1)、线段DF的长为;(2)、若AC交DF于点M,则 .三、解答题
-
15. 解方程: .16. 在坐标平面内,的顶点位置如图所示.

⑴将作平移变换,使得点变换成得到 .
⑵以点O为位似中心,在网格中画出与位似的图形 , 且使得与的相似比为 .
17. “大疫”当前,真情弥坚.新冠疫情发生后,全社会积极筹措群众急需的生活用品和防疫物资运往灾区,奉献爱心.已知运输物资的甲车组每天可行420千米,乙车组因故推迟2天出发,为了确保物资按时送达,乙车组以每天行630千米的速度前进,乙车组需要几天可以追上甲车组?18. 观察下列等式的规律:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
第5个等式:;
……
按照以上规律,解决下列问题:
(1)、写出第7个等式:;(2)、写出第n个等式(用含n的等式表示),并验证.19. 如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成.已知天桥高度BC≈4.8米,引桥水平跨度AC=8米.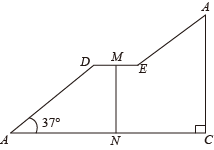
(参考:sin37°=0.60,cos37°=0.80,tan37°=0.75)
(1)、求水平平台DE的长度;(2)、若与地面垂直的平台立枉MN的高度为3米,求两段楼梯AD与BE的长度之比.20. 如图,的半径为1,A、B、C是上的三个点,点P在劣弧AB上, , PC平分 .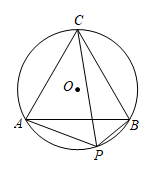 (1)、求证:;(2)、当点P位于什么位置时,的面积最大?求出最大面积.21. 疫情防控已成为常态化,为了解学生对疫情防控措施的知晓情况,某校保健室开展了“疫情防控知识”问卷测试(满分10分).他们将全校学生成绒进行统计,并随机抽取了40位同学的成绩绘制成如下的频数分布表和频数分布直方图(不完整).
(1)、求证:;(2)、当点P位于什么位置时,的面积最大?求出最大面积.21. 疫情防控已成为常态化,为了解学生对疫情防控措施的知晓情况,某校保健室开展了“疫情防控知识”问卷测试(满分10分).他们将全校学生成绒进行统计,并随机抽取了40位同学的成绩绘制成如下的频数分布表和频数分布直方图(不完整).组号
成绩
频数
频率
1
2
0.050
2
6
0.150
3
a
0.450
4
9
0.225
5
b
m
6
2
0.050
合计
40
1.000

根据以上提供的信息,解答下列问题:
(1)、表格中 , , ;补全频数分布直方图;(2)、这40位同学成绩的中位数落在哪一个小组?(3)、全校共有1200位同学参与测试,若以组中值(每组成绩的中间数值)为本组数据的代表,请估计所有同学成绩的平均分大约是多少?
