山西省百校联考(一)2022年中考模拟数学试题
试卷更新日期:2022-04-07 类型:中考模拟
一、单选题
-
1. 一5的绝对值是( )A、5 B、 C、 D、-52. 下列运算结果正确的是( )A、 B、 C、 D、3. 中国传统纹饰图案不但蕴含了丰富的文化,而且大多数图案还具有对称美.下列纹饰图案中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列调查中,适宜采用抽样调查的是( )A、调查某批次医用口罩的合格率 B、了解某校八年级一班学生的视力情况 C、了解100张百元钞票中有没有假钞 D、调查神舟十四号载人飞船各零部件的质量5. 通过严格实施低碳管理等措施,2022年北京冬奥会和冬残奥会全面实现了碳中和.根据测算,北京冬奥会三个赛区的场馆使用绿电4亿千瓦时,可以减少燃烧12.8万吨标准煤,减少排放二氧化碳32万吨,实现了“山林场馆、生态冬奥”的目标,其中的32万用科学记数法表示为( )
4. 下列调查中,适宜采用抽样调查的是( )A、调查某批次医用口罩的合格率 B、了解某校八年级一班学生的视力情况 C、了解100张百元钞票中有没有假钞 D、调查神舟十四号载人飞船各零部件的质量5. 通过严格实施低碳管理等措施,2022年北京冬奥会和冬残奥会全面实现了碳中和.根据测算,北京冬奥会三个赛区的场馆使用绿电4亿千瓦时,可以减少燃烧12.8万吨标准煤,减少排放二氧化碳32万吨,实现了“山林场馆、生态冬奥”的目标,其中的32万用科学记数法表示为( ) A、 B、 C、 D、6. 如图,在中, , 点是延长线上一点,过点作 . 若 , 则的度数为( )
A、 B、 C、 D、6. 如图,在中, , 点是延长线上一点,过点作 . 若 , 则的度数为( ) A、20° B、30° C、40° D、50°7. 不等式组的解集在数轴上表示正确的是( )A、
A、20° B、30° C、40° D、50°7. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 用配方法解方程 时,配方后所得的方程为( )A、 B、 C、 D、9. 已知点 , 均在反比例函数的图象上,且 , 则下列关系正确的是( )A、 B、 C、 D、10. 刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
8. 用配方法解方程 时,配方后所得的方程为( )A、 B、 C、 D、9. 已知点 , 均在反比例函数的图象上,且 , 则下列关系正确的是( )A、 B、 C、 D、10. 刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
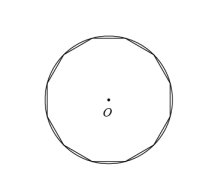 A、1 B、3 C、 D、
A、1 B、3 C、 D、二、填空题
-
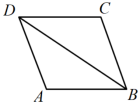
11. 计算: .12. 如图,在菱形中,连接 . 若 , 则的度数为°.
 13. 如图是4个外观完全相同的试剂瓶,分别装有稀硫酸溶液、稀盐酸溶液、氯化钠溶液、碳酸钠溶液.随机从这4瓶无标签试剂中抽取1瓶,抽到稀硫酸溶液的概率是 .
13. 如图是4个外观完全相同的试剂瓶,分别装有稀硫酸溶液、稀盐酸溶液、氯化钠溶液、碳酸钠溶液.随机从这4瓶无标签试剂中抽取1瓶,抽到稀硫酸溶液的概率是 . 14. 如图,网格中小正方形的边长都是1,若以格点为圆心,长为半径作 , 且点 , 均在格点上,则扇形的面积为 .
14. 如图,网格中小正方形的边长都是1,若以格点为圆心,长为半径作 , 且点 , 均在格点上,则扇形的面积为 . 15. 如图,在中, , 以为边作等边三角形 , 使点与点在同侧,连接 , 则 .
15. 如图,在中, , 以为边作等边三角形 , 使点与点在同侧,连接 , 则 .
三、解答题
-
16.(1)、计算: .(2)、解二元一次方程组:17. 如图,在四边形中, , , 点在的延长线上,点在的延长线上,且 , 连接 , . 求证:
 (1)、;(2)、 .18. 2021年12月9日“天宫课堂”第一课正式开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩!某校为了培养学生对航天知识的学习兴趣,组织全校800名学生进行了“航天知识竞赛”.教务处从中随机抽取了名学生的竞赛成绩(满分100分,每名学生的成绩记为分)分成四组,A组:;B组:;C组:;D组: , 并得到如下不完整的频数分布表、频数直方图和扇形统计图.根据图中信息,解答下列问题:
(1)、;(2)、 .18. 2021年12月9日“天宫课堂”第一课正式开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富在中国空间站进行太空授课,神奇的太空实验堪称宇宙级精彩!某校为了培养学生对航天知识的学习兴趣,组织全校800名学生进行了“航天知识竞赛”.教务处从中随机抽取了名学生的竞赛成绩(满分100分,每名学生的成绩记为分)分成四组,A组:;B组:;C组:;D组: , 并得到如下不完整的频数分布表、频数直方图和扇形统计图.根据图中信息,解答下列问题:
分组
频数
A:
B:
18
C:
24
D:
 (1)、的值为 , 的值为 , 的值为 .(2)、请补全频数直方图并计算扇形统计图中表示“C”的扇形圆心角的度数为 ▲ °.(3)、若规定学生竞赛成绩为优秀,请估算全校竞赛成绩达到优秀的学生人数.(4)、竞赛结束后,九年级一班从本班获得优秀的甲、乙、丙、丁四名同学中随机抽取两名宣讲航天知识.请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.19. “网上买年货,安心过大年”.2022年1月9日“全晋乐购”网上年货节启动.公众可通过多个电商平台参与减免、直降、秒杀等促销活动,享受无接触配送等服务.某网店专售一款中国结,其成本为每个40元,当销售单价为80元时,每天可销售100个.为了吸引更多顾客,该网店采取降价措施.据市场调查发现该款中国结销售单价每降1元,每天可多销售5个.设该款中国结的销售单价为元(为正整数),每天的销售量为个.
(1)、的值为 , 的值为 , 的值为 .(2)、请补全频数直方图并计算扇形统计图中表示“C”的扇形圆心角的度数为 ▲ °.(3)、若规定学生竞赛成绩为优秀,请估算全校竞赛成绩达到优秀的学生人数.(4)、竞赛结束后,九年级一班从本班获得优秀的甲、乙、丙、丁四名同学中随机抽取两名宣讲航天知识.请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.19. “网上买年货,安心过大年”.2022年1月9日“全晋乐购”网上年货节启动.公众可通过多个电商平台参与减免、直降、秒杀等促销活动,享受无接触配送等服务.某网店专售一款中国结,其成本为每个40元,当销售单价为80元时,每天可销售100个.为了吸引更多顾客,该网店采取降价措施.据市场调查发现该款中国结销售单价每降1元,每天可多销售5个.设该款中国结的销售单价为元(为正整数),每天的销售量为个. (1)、请直接写出与的函数关系式.(2)、当该网店每天销售利润为4500元时,求该款中国结的销售单价.20. 阅读下面材料,解答提出的问题.
(1)、请直接写出与的函数关系式.(2)、当该网店每天销售利润为4500元时,求该款中国结的销售单价.20. 阅读下面材料,解答提出的问题.德国著名数学家高斯在上小学时就已求出计算公式 , 其推导方法如下:
设 , ①
则 . ②
由①+②,得 ,
所以, .
即 .
(1)、请利用上述公式计算 .(2)、类比上述方法并证明: .(3)、若(其中为正整数),直接写出n的值.21. 某校数学兴趣小组开展综合实践活动——测量校园内旗杆的高度.如图,已知测倾器的高度为1.5米,在测点处安置测倾器,测得旗杆顶部点的仰角 , 在与点相距4.5米的点处安置测倾器,测得点的仰角(点 , , 在同一条水平线上,且点 , , , , , , 都在同一竖直平面内,点 , , 在同一直线上),求旗杆顶部离地面的高度 . (精确到0.1米,参考数据: , , ) 22. 问题情境:数学活动课上,老师出示了一个问题.如图1,在正方形中, , 分别以 , 为边在正方形内部作等边三角形与等边三角形 , 线段与交于点 , 线段与交于点 . 猜想与的数量关系,并加以证明.
22. 问题情境:数学活动课上,老师出示了一个问题.如图1,在正方形中, , 分别以 , 为边在正方形内部作等边三角形与等边三角形 , 线段与交于点 , 线段与交于点 . 猜想与的数量关系,并加以证明. (1)、数学思考:请解答老师出示的问题.(2)、深入探究:试判断四边形的形状,并加以证明.(3)、问题拓展:将从图1的位置开始沿射线的方向平移得到 , 连接 , . 当四边形是矩形时,得到图2.请直接写出平移的距离.23. 如图,已知抛物线与轴交于点和点 , 与轴交于点 . 连接 , .
(1)、数学思考:请解答老师出示的问题.(2)、深入探究:试判断四边形的形状,并加以证明.(3)、问题拓展:将从图1的位置开始沿射线的方向平移得到 , 连接 , . 当四边形是矩形时,得到图2.请直接写出平移的距离.23. 如图,已知抛物线与轴交于点和点 , 与轴交于点 . 连接 , .
 (1)、求抛物线的表达式,并直接写出所在直线的表达式.(2)、点为第四象限内抛物线上一点,连接 , , 求四边形面积的最大值及此时点的坐标.(3)、设点是所在直线上一点,且点的横坐标为 . 是否存在点 , 使为等腰三角形?若存在,直接写出的值;若不存在,请说明理由.
(1)、求抛物线的表达式,并直接写出所在直线的表达式.(2)、点为第四象限内抛物线上一点,连接 , , 求四边形面积的最大值及此时点的坐标.(3)、设点是所在直线上一点,且点的横坐标为 . 是否存在点 , 使为等腰三角形?若存在,直接写出的值;若不存在,请说明理由.