广东省2022年中考数学模拟测试题
试卷更新日期:2022-04-07 类型:中考模拟
一、单选题
-
1. 下列运算中,结果为负值的是( )A、 B、 C、 D、2. 已知有理数a、b在数轴上的位置如图所示,则下列结论中正确的是( )
 A、 B、 C、 D、3.
A、 B、 C、 D、3.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
 A、40° B、50° C、80° D、100°4. 对于数据:6,3,4,7,6,0,9.下列判断中正确的是( )A、这组数据的平均数是6,中位数是6 B、这组数据的平均数是6,中位数是7 C、这组数据的平均数是5,中位数是6 D、这组数据的平均数是5,中位数是75. 在一个不透明的口袋中装有2个红球,6个绿球,这些球除颜色外无其他差别,从这个袋子中随机摸出一个球摸到绿球的概率为( )A、1 B、 C、 D、6. 下列命题是真命题的是( )A、一组对边平行,且另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、四边都相等的矩形是正方形 D、对角线相等的四边形是矩形7. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A、40° B、50° C、80° D、100°4. 对于数据:6,3,4,7,6,0,9.下列判断中正确的是( )A、这组数据的平均数是6,中位数是6 B、这组数据的平均数是6,中位数是7 C、这组数据的平均数是5,中位数是6 D、这组数据的平均数是5,中位数是75. 在一个不透明的口袋中装有2个红球,6个绿球,这些球除颜色外无其他差别,从这个袋子中随机摸出一个球摸到绿球的概率为( )A、1 B、 C、 D、6. 下列命题是真命题的是( )A、一组对边平行,且另一组对边相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、四边都相等的矩形是正方形 D、对角线相等的四边形是矩形7. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )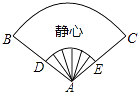 A、175πcm2 B、350πcm2 C、 πcm2 D、150πcm28. 如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
A、175πcm2 B、350πcm2 C、 πcm2 D、150πcm28. 如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )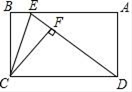 A、6 B、5 C、4 D、39. 一副三角板按图1所示的位置摆放,将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( )
A、6 B、5 C、4 D、39. 一副三角板按图1所示的位置摆放,将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( ) A、75cm2; B、(25+25)cm2; C、(25+)cm2; D、(25+)cm210. 对于二次函数y=ax2-(2a-1)x+a-1(a≠0),有下列结论:①其图象与x轴一定相交;②若a<0,函数在x>1时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中正确结论的个数是( )A、1 B、2 C、3 D、4
A、75cm2; B、(25+25)cm2; C、(25+)cm2; D、(25+)cm210. 对于二次函数y=ax2-(2a-1)x+a-1(a≠0),有下列结论:①其图象与x轴一定相交;②若a<0,函数在x>1时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中正确结论的个数是( )A、1 B、2 C、3 D、4二、填空题
-
11. 若 = ,则 的值为.12. 已知a﹣2b=10,则代数式a2﹣4ab+4b2的值为 .13. 如图,平行四边形ABCD中,点E是AD边上一点,连结EC、BD交于点F , 若AE:ED=5:4记△DFE的面积为S1 , △BCF的面积为S2 , △DCF的面积为S3 , 则DF:BF= , S1:S2:S3= .
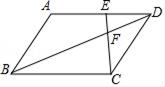 14. 如图,在 中,点 、 分别为边 、 的中点, 的平分线交线段 于点 ,若 , ,则线段 的长为.
14. 如图,在 中,点 、 分别为边 、 的中点, 的平分线交线段 于点 ,若 , ,则线段 的长为. 15. 某校八年级甲、乙两班举行电脑汉字输入比赛,两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如下表:
15. 某校八年级甲、乙两班举行电脑汉字输入比赛,两个班参加比赛的学生每分钟输入汉字的个数经统计和计算后结果如下表:班级
参加人数
平均字数
中位数
方差
甲
55
135
149
191
乙
55
135
151
110
有一位同学根据上面表格得出如下结论:
①甲、乙两班学生的平均水平相同;
②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);
③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是(填序号).
16. 已知实数a,b同时满足 , , 则b= .17. 如图,在矩形中,点、、分别在边、、、上,点P在矩形内,若 , , , , 四边形的面积为11,则四边形的面积为 .
三、解答题
-
18. 先化简 ,再任取一个你喜欢的x的值,代入求值。19. 如图,在Rt 中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt , 过点D作DE⊥CB,垂足为点E.
 (1)、依题意补全图形;(2)、求证: AC=PE;(3)、连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.20. 如图,在和中,为斜边, , 、相交于点 .
(1)、依题意补全图形;(2)、求证: AC=PE;(3)、连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.20. 如图,在和中,为斜边, , 、相交于点 .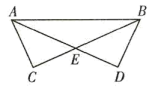 (1)、请说明的理由;(2)、若 , , 求的长.21. 某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):
(1)、请说明的理由;(2)、若 , , 求的长.21. 某商店一周内甲、乙两种计算器每天的销售量如下(单位:个):类别/星期
一
二
三
四
五
六
七
平均数
甲
3
4
4
3
4
5
5
乙
4
3
3
4
3
5
6
4
(1)、将表格填写完整.(2)、求甲种计算器本周销售量的方差.(3)、已知乙种计算器本周销售量的方差为 , 本周哪种计算器的销售量比较稳定?说明理由.22. 如图,AB是⊙O直径,BC⊥AB于点B,点C是射线BC上任意一点,过点C作CD切⊙O于点D,连接AD. (1)、求证:BC=CD;(2)、若∠C=60°,BC=3,求AD的长.23. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ).
(1)、求证:BC=CD;(2)、若∠C=60°,BC=3,求AD的长.23. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为BC边上的点,反比例函数y= (k≠0)在第一象限内的图象经过点D(m,2)和AB边上的点E(3, ).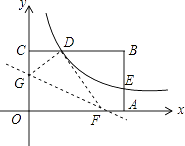 (1)、求反比例函数的表达式和m的值;(2)、将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.24. 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
(1)、求反比例函数的表达式和m的值;(2)、将矩形OABC的进行折叠,使点O于点D重合,折痕分别与x轴、y轴正半轴交于点F,G,求折痕FG所在直线的函数关系式.24. 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.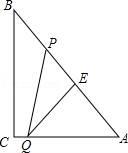 (1)、当t为何值时,PQ∥BC?(2)、设四边形PQCB的面积为y,求y关于t的函数关系式;(3)、四边形PQCB面积能否是△ABC面积的 ?若能,求出此时t的值;若不能,请说明理由;(4)、当t为何值时,△AEQ为等腰三角形?(直接写出结果)
(1)、当t为何值时,PQ∥BC?(2)、设四边形PQCB的面积为y,求y关于t的函数关系式;(3)、四边形PQCB面积能否是△ABC面积的 ?若能,求出此时t的值;若不能,请说明理由;(4)、当t为何值时,△AEQ为等腰三角形?(直接写出结果)