2022年广东省深圳市初中学业水平考试仿真模拟题
试卷更新日期:2022-04-07 类型:中考模拟
一、单选题
-
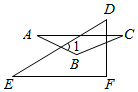
1. -2022的绝对值是( )A、2022 B、-2022 C、 D、2. 舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )A、4.995×1011 B、49.95×1010 C、0.4995×1011 D、4.995×10103. 下列运算正确的是( )A、 B、 C、 D、4. 将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为( )A、 B、 C、 D、5. 若点在第二象限,则a的取值范围是( )A、 B、 C、 D、6. 如图, , , ACEF,则的度数为( )
 A、 B、 C、 D、7. 下列命题正确的是( )A、方程x2﹣x+1=0有两个不相等实数根 B、对角线相等的四边形是矩形 C、平分弦的直径垂直于弦 D、等腰三角形底边上的中线平分顶角8. 某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满,设大房间有 个,小房间有 个.下列方程正确的是( )A、 B、 C、 D、9. 如果一个正整数能表示为两个正整数的平方差,那么这个正整数就称为“智慧数”,例如:5=32﹣22 , 5就是一个智慧数,则下列各数不是智慧数的是( )A、2020 B、2021 C、2022 D、202310. 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2 ;③S△CDF:S△BEF=9:4;④tan∠DCF= .其中正确的有( )
A、 B、 C、 D、7. 下列命题正确的是( )A、方程x2﹣x+1=0有两个不相等实数根 B、对角线相等的四边形是矩形 C、平分弦的直径垂直于弦 D、等腰三角形底边上的中线平分顶角8. 某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满,设大房间有 个,小房间有 个.下列方程正确的是( )A、 B、 C、 D、9. 如果一个正整数能表示为两个正整数的平方差,那么这个正整数就称为“智慧数”,例如:5=32﹣22 , 5就是一个智慧数,则下列各数不是智慧数的是( )A、2020 B、2021 C、2022 D、202310. 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2 ;③S△CDF:S△BEF=9:4;④tan∠DCF= .其中正确的有( )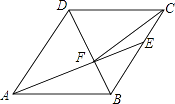 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 分解因式:2a3﹣8a= .12. 抛物线 的顶点坐标为 .13. 已知一元二次方程 有一个根为0,则a的值为.14. 在 中, , 平分 , 平分 , 相交于点 ,且 ,则 .
 15. 中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式 = 来表示二元一次方程组 ,而该方程组的解就是对应两直线(不平行)与a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式 = 所对应两直线交点坐标是 .
15. 中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式 = 来表示二元一次方程组 ,而该方程组的解就是对应两直线(不平行)与a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式 = 所对应两直线交点坐标是 .三、解答题
-
16. 计算17. 解不等式组 , 并利用数轴确定不等式组的解集.
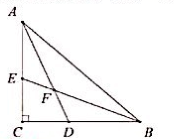
 18. 父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.(1)、求爸爸吃到一个花生馅汤圆,一个芝麻馅汤圆的概率;(2)、若给爸爸再增加一个花生馅的汤圆,则爸爸吃到一个花生馅汤圆,一个芝麻馅汤圆的可能性是否会增大?请说明理由.19. 图1是某种路灯的实物图片,图2是该路灯的平面示意图, 为立柱的一部分,灯臂 ,支架 与立柱 分别交于A,B两点,灯臂 与支架 交于点C,已知 , , ,求支架 的长.(结果精确到 ,参考数据: , , )
18. 父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.(1)、求爸爸吃到一个花生馅汤圆,一个芝麻馅汤圆的概率;(2)、若给爸爸再增加一个花生馅的汤圆,则爸爸吃到一个花生馅汤圆,一个芝麻馅汤圆的可能性是否会增大?请说明理由.19. 图1是某种路灯的实物图片,图2是该路灯的平面示意图, 为立柱的一部分,灯臂 ,支架 与立柱 分别交于A,B两点,灯臂 与支架 交于点C,已知 , , ,求支架 的长.(结果精确到 ,参考数据: , , )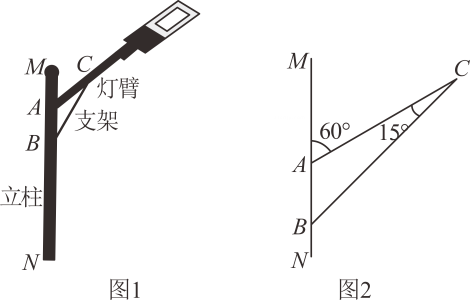 20. 如图,直线y1=ax+b与双曲线y2= 交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).
20. 如图,直线y1=ax+b与双曲线y2= 交于A,B两点,与x轴交于点C,点A的纵坐标为6,点B的坐标为(﹣3,﹣2).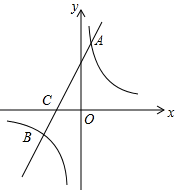 (1)、求直线和双曲线的解析式;(2)、根据图象直接写出ax+b﹣ >0中x的取值范围.21. 如图1,在平面直角坐标系中,已知点 , 以O为圆心,OA为半径作 , 交y轴于点C,直线l:经过点C.
(1)、求直线和双曲线的解析式;(2)、根据图象直接写出ax+b﹣ >0中x的取值范围.21. 如图1,在平面直角坐标系中,已知点 , 以O为圆心,OA为半径作 , 交y轴于点C,直线l:经过点C. (1)、设直线l与的另一个交点为如图 , 求弦CD的长;(2)、将直线l向上平移2个单位,得直线m,如图2,求证:直线m与相切;(3)、在的前提下,设直线m与切于点P,Q为上一动点,过点P作 , 交直线QA于点如图 , 则的最大面积为 .22. 如图1.抛物线与轴交于A、两点.交轴于点 , 点 , 连接 .
(1)、设直线l与的另一个交点为如图 , 求弦CD的长;(2)、将直线l向上平移2个单位,得直线m,如图2,求证:直线m与相切;(3)、在的前提下,设直线m与切于点P,Q为上一动点,过点P作 , 交直线QA于点如图 , 则的最大面积为 .22. 如图1.抛物线与轴交于A、两点.交轴于点 , 点 , 连接 .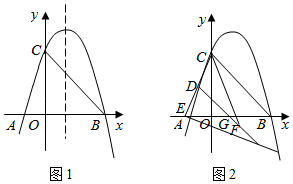 (1)、求抛物线的解析式;(2)、为抛物线上一点,点为轴上一点,点在轴上,求的最小值;(3)、如图2.点是抛物线上一点,为第四象限抛物线上一点,延长交轴于点 , 连接 , 点 , 直线与交于点 , 点在线段上,且 , 已知 , 求点的坐标.
(1)、求抛物线的解析式;(2)、为抛物线上一点,点为轴上一点,点在轴上,求的最小值;(3)、如图2.点是抛物线上一点,为第四象限抛物线上一点,延长交轴于点 , 连接 , 点 , 直线与交于点 , 点在线段上,且 , 已知 , 求点的坐标.