初中数学人教版八年级下学期备考期中考试压轴题
试卷更新日期:2022-04-06 类型:复习试卷
一、解答题
-
1. 已知 + + +…+ = ,求n的值.2. 阅读理解
“分母有理化”是我们常用的一种化简的方法: ,除此之外,我们也可以用平方之后再开方的方式来化简一些有特点的无理数,如:对于
设 ,
易知
故 ,由
解得 ,即 .
根据以上方法,化简
3. 已知 的三边长为 , , ,化简 .4. 如图,以直角三角形AOC 的直角顶点O为原点,以 OA,OC 所在直线为x轴,y轴建立平面直角坐标系,点 满足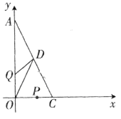 (1)、则 点的坐标为; 点的坐标为.(2)、直角三角形 的面积为.(3)、已知坐标轴上有两动点 同时出发, 点从 点出发沿 轴负方向以1个单位长度每秒的速度匀速移动, 点从 点出发以2个单位长度每秒的速度沿 轴正方向移动,点 到达 点整个运动随之结束. 的中点 的坐标是 ,设运动时间为t(t>0)秒,问:是否存在这样的t使 ?若存在,请求出 的值;若不存在,请说明理由.5. 先阅读下面材料,然后再根据要求解答提出的问题:
(1)、则 点的坐标为; 点的坐标为.(2)、直角三角形 的面积为.(3)、已知坐标轴上有两动点 同时出发, 点从 点出发沿 轴负方向以1个单位长度每秒的速度匀速移动, 点从 点出发以2个单位长度每秒的速度沿 轴正方向移动,点 到达 点整个运动随之结束. 的中点 的坐标是 ,设运动时间为t(t>0)秒,问:是否存在这样的t使 ?若存在,请求出 的值;若不存在,请说明理由.5. 先阅读下面材料,然后再根据要求解答提出的问题:设a、b是有理数,且满足 ,求 的值?
解: 由题意得: ,
因为a、b都是有理数,
所以a-3、b+2也是有理数,
由于 是无理数,
所以a-3=0、b+2=0,
所以a=3、b=-2,
所以 ,
问题: 设x、y都是有理数,且满足 ,求x+y的值,
6. 如图,在平面直角坐标系中,点A,B,c的坐标分别为A(0,m),B(-5,0),C(n,0),且(n-3)²+ =0.一动点P从点B出发,以每秒2单位长度的速度沿射线B0匀速运动,设点P运动的时间为ts. (1)、求A,C两点的坐标;(2)、连接PA,若∆PAB为等腰三角形,求点P的坐标;(3)、当点P在线段B0上运动时间t= ▲ s时,使△AOP≌△AOC?(请直接写出t的值,不需说明理由)7. 如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.
(1)、求A,C两点的坐标;(2)、连接PA,若∆PAB为等腰三角形,求点P的坐标;(3)、当点P在线段B0上运动时间t= ▲ s时,使△AOP≌△AOC?(请直接写出t的值,不需说明理由)7. 如图,将矩形ABCD沿EF折叠,使点C恰好落在AB边的中点C'上,点D落在D'处,C'D'交AE于点M.若AB=6,BC=9,求线段ED.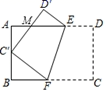 8. 如图,在等边 中,点 (2,0),点 是原点,点 是 轴正半轴上的动点,以 为边向左侧作等边 ,当 时,求 的长.
8. 如图,在等边 中,点 (2,0),点 是原点,点 是 轴正半轴上的动点,以 为边向左侧作等边 ,当 时,求 的长. 9. 中, , , , 分别是边 和 上的动点,在图中画出 值最小时的图形,并直接写出 的最小值为.
9. 中, , , , 分别是边 和 上的动点,在图中画出 值最小时的图形,并直接写出 的最小值为. 10. △ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2 , 若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.
10. △ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2 , 若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.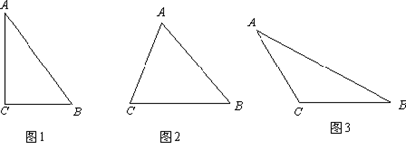 11. 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?
11. 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D.若AB=3cm,BC=5cm,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△ABP为等腰三角形?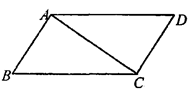 12. 小明同学在做作业时,遇到如下问题:如图1,已知:等边△ABC,点D在BC上,以AD为边作等边△ADE,连接CE,求证:∠ACE=60°.
12. 小明同学在做作业时,遇到如下问题:如图1,已知:等边△ABC,点D在BC上,以AD为边作等边△ADE,连接CE,求证:∠ACE=60°. (1)、请你解答小明的这道题;(2)、在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?
(1)、请你解答小明的这道题;(2)、在这个问题中,当D在BC上运动时,点E是否在一条线段上运动?(直接答“是”或“不是”)
(3)、如图2,正方形ABCD的边长为2,E是直线BC上的一个动点,以DE为边作正方形DEFG(DEFG按逆时针排列)。当E在直线BC上运动时,点G是否在一条直线上运动?如果是,请你画出这条直线并证明;如果不是,也请说明理由;(4)、连接AG、CG,①求证:AG2-CE2是定值; ②求AG+CG的最小值(直接写出答案即可)。13. 一、阅读理解:在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
14. 在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的. (1)、(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).(2)、(验证猜想)同学们讨论得出下列三种证明思路(如图1):
(1)、(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).(2)、(验证猜想)同学们讨论得出下列三种证明思路(如图1):思路一:过点A作 ,交CD的延长线于点G.
思路二:过点A作 ,并截取 ,连接DG.
思路三:延长CD至点G,使 ,连接AG.
请选择你喜欢的一种思路证明(探究发现)中的结论.
(3)、(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且 , ,设 ,试用含 的代数式表示DF的长.15. 如图,在矩形 中, , ,若点M、N分别是线段 、 上的两个动点,则求 的最小值. 16. 如图,△ABC是边长为10的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合).
16. 如图,△ABC是边长为10的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合).
(Ⅰ)如图1,若点Q是BC边上一动点,与点P同时以相同的速度由C向B运动(与C、B不重合).求证:BP=AQ;
(Ⅱ)如图2,若Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E , 连接PQ交AB于D , 在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生改变,请说明理由.
17. 如图1,点C在线段AB上,分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN,连结AM、BD.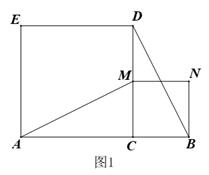 (1)、AM与BD的关系是: .(2)、如果将正方形BCMN绕点C顺时针旋转锐角α,它不变(如图2).(1)中所得的结论是否仍然成立?请说明理由.
(1)、AM与BD的关系是: .(2)、如果将正方形BCMN绕点C顺时针旋转锐角α,它不变(如图2).(1)中所得的结论是否仍然成立?请说明理由. (3)、在(2)的条件下,连接AB、DM,若AC=4,BC=2,求 的值.18. 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(3)、在(2)的条件下,连接AB、DM,若AC=4,BC=2,求 的值.18. 如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.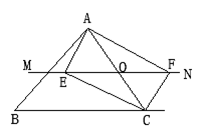 (1)、求证:EO=FO;(2)、当点O运动到何处时,四边形AECF是矩形?并证明你的结论;(3)、若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。19. 如图,在Rt△ABC中,∠B=90°,AC=12,∠A=60°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)、求证:EO=FO;(2)、当点O运动到何处时,四边形AECF是矩形?并证明你的结论;(3)、若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。19. 如图,在Rt△ABC中,∠B=90°,AC=12,∠A=60°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF. (1)、AB的长是 .(2)、在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.(3)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.20.
(1)、AB的长是 .(2)、在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.(3)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.20.定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
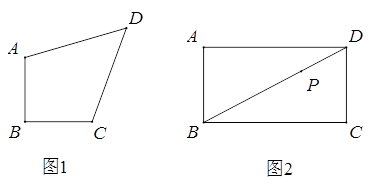 (1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
(1)、如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)、如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.21. 如图,四边形ABCD为菱形,∠BAD=60°,E为直线BD上的动点(点E不与点B和点D重合),直线CE绕C点顺时针旋转60°与直线AD相交于点F,连接EF.(1)如图①,当点E在线段BD上时,∠CEF= 度;
(2)如图②,当点E在BD延长线上时,试判断∠DEF+∠DFE与∠CEF度数之间的关系,并说明理由;
(3)如图③,若四边形ABCD为平行四边形,∠DBC=∠DCB=45°,E为直线BD上的动点(点E不与点B和点D重合),射线CE绕C点顺时针旋转45°与直线AD相交于点F,连接EF,探究∠DEF+∠DFE与∠CEF度数之间的关系.(直接写出结果)
 22. 如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
22. 如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
23. (1)如图1,在平行四边形ABCD中,对角线AC、BD相交于O点,过点O的直线l与边AB、CD分别交于点E、F,绕点O旋转直线l,猜想直线l旋转到什么位置时,四边形AECF是菱形.证明你的猜想.(2)若将(1)中四边形ABCD改成矩形ABCD,使AB=4cm,BC=3cm,
①如图2,绕点O旋转直线l与边AB、CD分别交于点E、F,将矩形ABCD沿EF折叠,使点A与点C重合,点D的对应点为D′,连接DD′,求△DFD′的面积.
②如图3,绕点O继续旋转直线l,直线l与边BC或BC的延长线交于点E,连接AE,将矩形ABCD沿AE折叠,点B的对应点为B′,当△CEB′为直角三角形时,求BE的长度.请直接写出结果,不必写解答过程.
 24.
24.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
 25. 阅读下面材料:
25. 阅读下面材料:
小明遇到这样一个问题:如图1,在边长为的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)


请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 , 则AD的长为__________.


