2022年中考数学二轮专题复习-等腰三角形、直角三角形及解直角三角形
试卷更新日期:2022-04-06 类型:二轮复习
一、单选题
-
1. 在中, , , 则的值是( )A、 B、 C、 D、2. 如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为a,则两梯脚之间的距离BC为( )
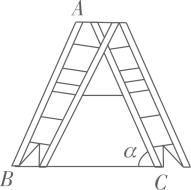 A、4cos a B、4sin a C、4tan a D、3. 如图,中, , , 若将绕点逆时针旋转得到 , 连接 , 则在点运动过程中,线段的最小值为( )
A、4cos a B、4sin a C、4tan a D、3. 如图,中, , , 若将绕点逆时针旋转得到 , 连接 , 则在点运动过程中,线段的最小值为( ) A、1 B、 C、 D、24. 如图,在ABC中,AB=AC,D是BC的中点,∠B=35°,则∠BAD=( )
A、1 B、 C、 D、24. 如图,在ABC中,AB=AC,D是BC的中点,∠B=35°,则∠BAD=( )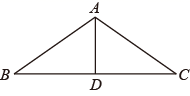 A、110° B、70° C、55° D、35°5. 如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )
A、110° B、70° C、55° D、35°5. 如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )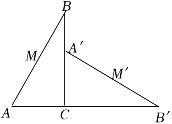 A、6 B、2π C、3π D、4π6. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交AC于点D,交BC于点E,交BA的延长线于点F,若 ,则BF的长为( )
A、6 B、2π C、3π D、4π6. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交AC于点D,交BC于点E,交BA的延长线于点F,若 ,则BF的长为( )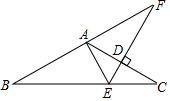 A、 B、3 C、 D、7. 如图,已知点D,E,F分别在△ABC的三边上,将△ABC沿DE,DF翻折,顶点B,C均落在△ABC内的点O处,且BD与CD重合于线段OD,若∠AEO+∠AFO=58°,则∠A的度数为( )
A、 B、3 C、 D、7. 如图,已知点D,E,F分别在△ABC的三边上,将△ABC沿DE,DF翻折,顶点B,C均落在△ABC内的点O处,且BD与CD重合于线段OD,若∠AEO+∠AFO=58°,则∠A的度数为( )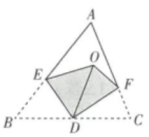 A、58° B、59° C、60° D、61°8. 已知 为圆 的直径, 为圆周上一点, , .则 的度数为( )
A、58° B、59° C、60° D、61°8. 已知 为圆 的直径, 为圆周上一点, , .则 的度数为( ) A、10° B、15° C、20° D、30°9. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A、10° B、15° C、20° D、30°9. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )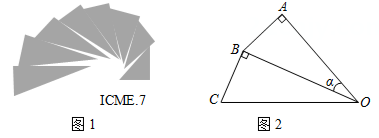 A、 B、 C、 D、10. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于 MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
A、 B、 C、 D、10. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于 MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( ) A、8 B、7 C、6 D、511. 如图,四边形ABCD是一张平行四边形纸片,其高AG=2cm,底边BC=6cm,∠B=45°,沿虚线EF将纸片剪成两个全等的梯形,若∠BEF=30°,则AF的长为( )
A、8 B、7 C、6 D、511. 如图,四边形ABCD是一张平行四边形纸片,其高AG=2cm,底边BC=6cm,∠B=45°,沿虚线EF将纸片剪成两个全等的梯形,若∠BEF=30°,则AF的长为( )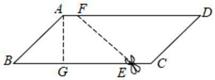 A、1cm B、 cm C、(2 ﹣3)cm D、(2﹣ )cm12. 如图,明年舟山将再添一个最高颜值城市新地标,新城长峙岛上将矗立起一座摩天轮,其直径为90m,旋转1周用时15min.小明从摩天轮的底部(与地面相距0.5m)出发开始观光,摩天轮转动1周,小明在离地面68m以上的空中有多长时间?( )
A、1cm B、 cm C、(2 ﹣3)cm D、(2﹣ )cm12. 如图,明年舟山将再添一个最高颜值城市新地标,新城长峙岛上将矗立起一座摩天轮,其直径为90m,旋转1周用时15min.小明从摩天轮的底部(与地面相距0.5m)出发开始观光,摩天轮转动1周,小明在离地面68m以上的空中有多长时间?( ) A、3min B、5min C、6min D、10min13. 如图,在 中, , , 为 边的中点, , 绕 点旋转,它的两边分别交 和 的延长线于 , ,当点 在 延长线上时, , , 的关系为( )
A、3min B、5min C、6min D、10min13. 如图,在 中, , , 为 边的中点, , 绕 点旋转,它的两边分别交 和 的延长线于 , ,当点 在 延长线上时, , , 的关系为( ) A、 = B、 = C、 = D、 =14. 如图, 中, , ,点D是边 上一动点,连接 ,以 为直径的圆交 于点E.若 长为4,则线段 长的最小值为( )
A、 = B、 = C、 = D、 =14. 如图, 中, , ,点D是边 上一动点,连接 ,以 为直径的圆交 于点E.若 长为4,则线段 长的最小值为( ) A、 B、 C、 D、15. 如图,ABC和ECD都是等腰直角三角形,∠ACB=∠DCE=90°,ABC的顶点A在ECD的斜边DE上.下列结论不正确的是( )
A、 B、 C、 D、15. 如图,ABC和ECD都是等腰直角三角形,∠ACB=∠DCE=90°,ABC的顶点A在ECD的斜边DE上.下列结论不正确的是( )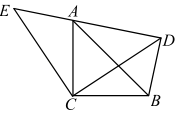 A、ACE≌BCD B、∠DAB=45° C、AD+DB=DE D、ABD是直角三角形16. 如图, 中, , , ,垂足为Q,延长MN至G,取 ,若 的周长为12, ,则 周长是( )
A、ACE≌BCD B、∠DAB=45° C、AD+DB=DE D、ABD是直角三角形16. 如图, 中, , , ,垂足为Q,延长MN至G,取 ,若 的周长为12, ,则 周长是( )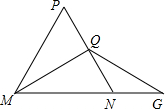 A、8+2m B、8+m C、6+2m D、6+m17. 如图,已知四边形 是边长为4的正方形,以对角线 为边作正三角形 ,过点 作 ,交 的延长线于点 ,则 的长是( )
A、8+2m B、8+m C、6+2m D、6+m17. 如图,已知四边形 是边长为4的正方形,以对角线 为边作正三角形 ,过点 作 ,交 的延长线于点 ,则 的长是( )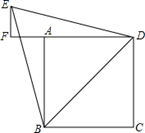 A、 B、 C、 D、18. 如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( )
A、 B、 C、 D、18. 如图,将一个等腰直角三角形△ABC按如图方式折叠,若DE=a,DC=b,下列四个结论:①DC′平分∠BDE;②BC长为2a+b;③△BDC′是等腰三角形;④△CED的周长等于BC的长.其中,正确的是( ) A、①②④ B、②③④ C、②③ D、②④19. 著名画家达·芬奇用三个正方形和三个全等的直角三角形拼成如下图形证明了勾股定理,其中 ,连结HF,CJ,得到4个全等的四边形HFGI,四边形HFBA,四边形CJEA,四边形JCBD.CJ分别交AB,ED于点M,N,若 ,且 ,则HF的长为( )
A、①②④ B、②③④ C、②③ D、②④19. 著名画家达·芬奇用三个正方形和三个全等的直角三角形拼成如下图形证明了勾股定理,其中 ,连结HF,CJ,得到4个全等的四边形HFGI,四边形HFBA,四边形CJEA,四边形JCBD.CJ分别交AB,ED于点M,N,若 ,且 ,则HF的长为( ) A、 B、 C、 D、20. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
A、 B、 C、 D、20. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )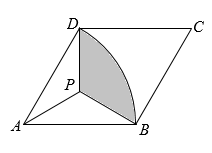 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
21. 如图,在△ABC中, AB=AC ,BC=3+ ,∠BAC=90°,点D、E都在边BC上,∠DAE=45°.若BD=2CE,则DE的长是。
 22. 疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.
22. 疫情期间,小红在家里在图1所示的平板支架上网课,图2是她观看网课的侧面示意图,已知平板宽度AB=20cm,支架底板宽度CD=AB,支撑角∠ABC=60°,支撑板CE=BE=6cm,小红坐在距离支架底板20cm处观看(即DF=20cm),Q点是AB中点.当视线PQ与屏幕AB垂直时,小红的眼睛距离桌面的高度PF等于 cm;当落在屏幕中点的视线与屏幕构成的夹角(指锐角或直角)不小于75°时,能使观看平板视频的效果最佳,为保证最佳的观看效果,小红眼睛距离桌面的最大高度和最小高度的差等于 cm.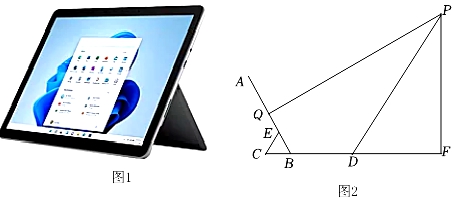 23. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.
23. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.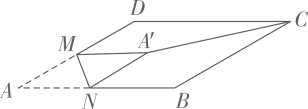 24. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π).
24. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π).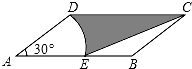 25. 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,则建筑物的高度米.(测角器的高度忽略不计,结果精确到0.1米)(参考数据:sin48°≈ ,tan48°≈ ,sin64°≈ ,tan64°≈2)
25. 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,则建筑物的高度米.(测角器的高度忽略不计,结果精确到0.1米)(参考数据:sin48°≈ ,tan48°≈ ,sin64°≈ ,tan64°≈2) 26. 如图,把一副三角板按如图放置,∠ACB=∠ADB=90°,∠CAB=30°,∠DAB=45°,点E是AB的中点,连结CE,DE,DC.若AB=6,则∆DEC的面积为
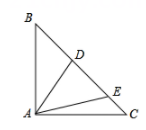
26. 如图,把一副三角板按如图放置,∠ACB=∠ADB=90°,∠CAB=30°,∠DAB=45°,点E是AB的中点,连结CE,DE,DC.若AB=6,则∆DEC的面积为 27. 如图,在 中, ,延长线段BC至点 使 ,连接AD.若点 是线段BC上一个动点,过点 作 交AB于点 ,连接AP,则当 的面积最大时,BP的长度为.
27. 如图,在 中, ,延长线段BC至点 使 ,连接AD.若点 是线段BC上一个动点,过点 作 交AB于点 ,连接AP,则当 的面积最大时,BP的长度为.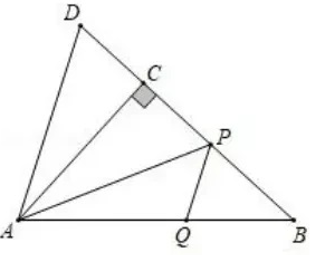 28. 图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+ , 则图3中线段AB的长为.
28. 图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+ , 则图3中线段AB的长为. 29. 如图,在△AB1C1中,AC1=B1C1 , ∠C1=20°,在B1C1上取一点C2 , 延长AB1到点B2 , 使得B1B2=B1C2 , 在B2C2上取一点C3 , 延长AB2到点B3 , 使得B2B3=B2C3 , 在B3C3上取一点C4 , 延长AB3到点B4 , 使得B3B4=B3C4 , ……,按此操作进行下去,那么第2个三角形的内角∠AB2C2=°;第n个三角形的内角∠ABnCn=°.
29. 如图,在△AB1C1中,AC1=B1C1 , ∠C1=20°,在B1C1上取一点C2 , 延长AB1到点B2 , 使得B1B2=B1C2 , 在B2C2上取一点C3 , 延长AB2到点B3 , 使得B2B3=B2C3 , 在B3C3上取一点C4 , 延长AB3到点B4 , 使得B3B4=B3C4 , ……,按此操作进行下去,那么第2个三角形的内角∠AB2C2=°;第n个三角形的内角∠ABnCn=°.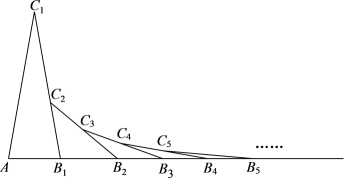 30. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号:
30. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号:
三、解答题
-
31. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.
 32. 某一天,小明和小亮想利用所学过的测量知识来测量G棵古树的高度AB.他们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示,于是他们先在古树周围的空地上选择一点D,通过测倾器测得树的顶端A的仰角为45°,再在BD的延长线上确定一点F,使DF=5米,并在F处通过测倾器测得树的顶端A的仰角为30°,测倾器的高度CD=EF=1米已知点FD、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(结果保留根号)
32. 某一天,小明和小亮想利用所学过的测量知识来测量G棵古树的高度AB.他们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示,于是他们先在古树周围的空地上选择一点D,通过测倾器测得树的顶端A的仰角为45°,再在BD的延长线上确定一点F,使DF=5米,并在F处通过测倾器测得树的顶端A的仰角为30°,测倾器的高度CD=EF=1米已知点FD、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(结果保留根号)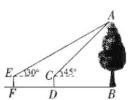 33. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
33. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)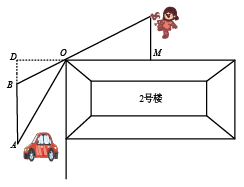 34. 探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
34. 探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE. (1)、当∠BAD=60°时,求∠CDE的度数;(2)、当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;(3)、深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.35. 如图是一个小商场的纵截面图(矩形 ), 是商场的顶部, 是商场的地面,地面由边长为 的正方形瓷砖铺成,从 到 共有 块瓷砖, 和 是商场的两面墙壁, 是顶部正中央的一个长方形的灯饰( ).小张同学想通过学过的几何知识来测量该商场的高度( )和灯饰的长度( ),于是去商场时带了一块镜子和一根激光笔,他先把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 两块砖的 处,发现激光笔的反射光照到了 处;再把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 三块砖的 处,发现激光笔的反射光恰好又照到了 处,请你帮忙计算 的高度和 的长度.
(1)、当∠BAD=60°时,求∠CDE的度数;(2)、当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;(3)、深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.35. 如图是一个小商场的纵截面图(矩形 ), 是商场的顶部, 是商场的地面,地面由边长为 的正方形瓷砖铺成,从 到 共有 块瓷砖, 和 是商场的两面墙壁, 是顶部正中央的一个长方形的灯饰( ).小张同学想通过学过的几何知识来测量该商场的高度( )和灯饰的长度( ),于是去商场时带了一块镜子和一根激光笔,他先把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 两块砖的 处,发现激光笔的反射光照到了 处;再把激光笔挂在墙壁 距地面两块砖高度( 的长)的 处,镜子水平放在地面距离 三块砖的 处,发现激光笔的反射光恰好又照到了 处,请你帮忙计算 的高度和 的长度. 36. 问题背景:如图1,等腰△ABC中,AB=AC , ∠BAC=120°,作AD⊥BC于点D , 则D为BC的中点,∠BAD= ∠BAC=60°,于是 = = ;
36. 问题背景:如图1,等腰△ABC中,AB=AC , ∠BAC=120°,作AD⊥BC于点D , 则D为BC的中点,∠BAD= ∠BAC=60°,于是 = = ;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D , E , C三点在同一条直线上,连接BD .

①求证:△ADB≌△AEC;
②请直接写出线段AD , BD , CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM , 作点C关于BM的对称点E , 连接AE并延长交BM于点F , 连接CE , CF .
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
37. 将两个等腰直角三角形纸片 和 放在平面直角坐标系中,已知点A坐标为 , , , ,并将会 绕点O顺时针旋转.
(Ⅰ)当旋转至如图①的位置时, ,求此时点C的坐标;(Ⅱ)如图②,连接 ,当 旋转到y轴的右侧,且点B , C , D三点在一条直线上时,求 的长;
(Ⅲ)当旋转到使得 的度数最大时,求 的面积(直接写出结果即可).
四、综合题
-
38. 爱好思考的小实在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”,如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC=b,AB=c.
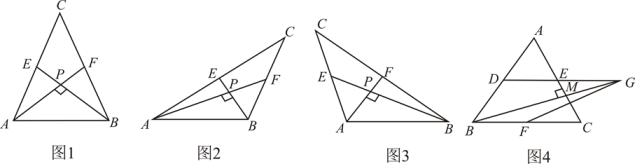 (1)、【特例探究】
(1)、【特例探究】①如图1,当tan∠PAB=1, 时,a= , b=.
②如图2,当∠PAB=30°,c=4时,a= , b=.
(2)、【归纳证明】请你观察(1)中的计算结果,猜想 、 、 三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)、【拓展证明】如图4,在△ABC中, , ,D、E、F分别是边AB、AC、BC的中点,连结DE并延长至点G,使得GE=DE,连结BG.若BG⊥AC于点M时,求GF的长.
39. 如图, 是边长为 的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是 ,当点 到达点 时,P,Q两点停止运动,设点 的运动时间为 ,解答下列问题: (1)、求 的面积.(2)、当 为何值时, 是直角三角形?(3)、是否存在某一时刻 ,使四边形APQC的面积是 面积的 ?如果存在,求出 的值;如果不存在,请说明理由.
(1)、求 的面积.(2)、当 为何值时, 是直角三角形?(3)、是否存在某一时刻 ,使四边形APQC的面积是 面积的 ?如果存在,求出 的值;如果不存在,请说明理由.