浙江省金华市六校联谊2022年模拟考试数学试卷
试卷更新日期:2022-04-06 类型:中考模拟
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. -6的倒数是A、6 B、-6 C、 D、
-
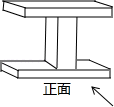
2. 如图,该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
3. 我们的祖国地域辽阔,其中领水面积约为 .把370000这个数用科学记数法表示为A、 B、 C、 D、
-
4. 下列计算不正确的是( )A、a2•a3=a5 B、(a2)3=a6 C、a3÷a2=a D、a3+a3=a6
-
5. 将二次函数y=x2的图象向左平移1个单位,再向上平移2个单位后,所得图象的函表达式是( )A、y=(x﹣1)2+2 B、y=(x+1)2+2 C、y=(x﹣1)2﹣2 D、y=(x+1)2﹣2
-
6. 在平面直角坐标系中,点 关于 轴对称的点的坐标是A、 B、 C、 D、
-
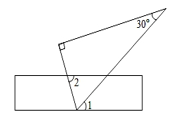
7. 一把直尺与含30°的直角三角板如图所示放置,∠1=40°,则∠2的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
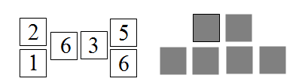
8. 如图,有一些写有号码的卡片,它们的背面都相同,现将它们背面朝上,从中任意摸出一张,摸到6号卡片的概率是( )
 A、
A、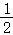 B、
B、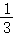 C、
C、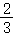 D、
D、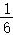
-
9. 如图将一个三角板放在⊙O上,使三角板的一直角边经过圆心O,两直角边与⊙O交于点B和点C,测得AC=5cm,AB=3cm,则⊙O的半径长为( )
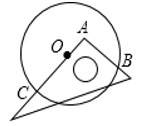 A、4cm B、3.5cm C、2.85cm D、3.4cm
A、4cm B、3.5cm C、2.85cm D、3.4cm -
10. 如图,正方形 边长为4,点 在边 上运动(不含端点),以 为边作等腰直角三角形 ,∠AEF= ,连接 .下面四个说法中有几个正确( )
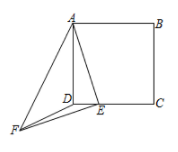
①当 时, ;②当 时,点 , , 共线;③当三角形 与三角形 面积相等时,则DE= ;④当 平分∠EAF时,则DE= .
A、1个 B、2个 C、3个 D、4个
二、填空题:本题共6小题,每小题4分,共24分。
-
11. 函数 中自变量x的取值范围是.
-
12. 分解因式:
-
13. 数据1,2,4,5,3,6的中位数是 .
-
14. 小明用图1中的一副七巧板拼出如图2所示的“火箭图”,若正方形ABCD的边长为4cm,则图2中M与N两点之间的距离为 cm.

-
15. 如图,15个形状大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角为60°,A、B、C都在格点上,点D在过A、B、C三点的圆弧上,若E也在格点上,且∠AED=∠ACD,则cos∠AEC= .

-
16. 如图在矩形ABCD中,AB=6,AD=8,E为对角线AC上的动点,EF⊥DE交BC边于点F,以DE,EF为邻边作矩形DEFG.
 (1)、当AE=2时,求 ;(2)、点H在AD上且HD=3,连接HG,则HG的取值范围是.
(1)、当AE=2时,求 ;(2)、点H在AD上且HD=3,连接HG,则HG的取值范围是.
三、解答题(本题有8小题,共66分)
-
17. 计算:
-
18. 解方程
-
19. 在疫情期间,某校开展线上教学的模式,为学生提供四类在线学习方式:A(在线阅读)、B(在线听课)、C(在线答疑)、D(在线讨论),为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查(每人只能选一类),并根据调查结果绘制成如图所示两幅不完整的统计图.
 (1)、本次调查的人数是 , C在扇形统计图中的圆心角度数为 度;(2)、请补全条形统计图;(3)、若该校共有学生1200人,请你估计对“在线听课”最感兴趣的学生人数;
(1)、本次调查的人数是 , C在扇形统计图中的圆心角度数为 度;(2)、请补全条形统计图;(3)、若该校共有学生1200人,请你估计对“在线听课”最感兴趣的学生人数; -
20. 如图在5×5的网格中,△ABC的顶点都在格点上.(仅用无刻度的直尺在给定的网格中按要求画图,画图过程用虚线表示,画图结果用实线表示)
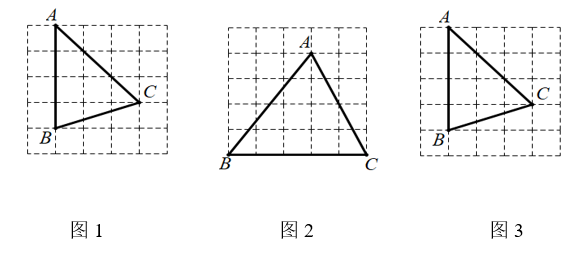 (1)、在图1中画出△ABC的中线AD;(2)、在图2中画线段CE,点E在AB上,使得 : =2 : 3;(3)、在图3中画出△ABC的外心点O.
(1)、在图1中画出△ABC的中线AD;(2)、在图2中画线段CE,点E在AB上,使得 : =2 : 3;(3)、在图3中画出△ABC的外心点O. -
21. 如图,AB为⊙O的直径,C、F为⊙O上两点,且点C为弧BF的中点,过点C作AF的垂线,交AF的延长线于点E,交AB的延长线于点D.
 (1)、求证:DE是⊙O的切线;(2)、如果半径的长为3,tanD= ,求AE的长.
(1)、求证:DE是⊙O的切线;(2)、如果半径的长为3,tanD= ,求AE的长. -
22. 为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时 千米的道路 (如图所示),当无人机在限速道路的正上方 处时,测得限速道路的起点 的俯角是 ,无人机继续向右水平飞行 米到达 处,此时又测得起点 的俯角是 ,同时测得限速道路终点 的俯角是 (注: ).(参考数据: , , )
 (1)、求无人机离道路AB的高度(结果保留根号);(2)、如果李师傅在道路 上行驶的时间是 分 秒,请判断他是否超速?并说明理由.( )
(1)、求无人机离道路AB的高度(结果保留根号);(2)、如果李师傅在道路 上行驶的时间是 分 秒,请判断他是否超速?并说明理由.( ) -
23. 某班“数学兴趣小组”对函数y= 的图象和性质进行了探究,探究过程如下,请补充完成:(1)、下表是y与x的几组对应值,请直接写出m,n的值:m=;n=.
x
-2
-1
0
n
2
3
4
y
m
0
-1
-3
5
3
2
(2)、如图在平面直角坐标系中,描出了以上表格中的对应值为坐标的一些点,请再描出其它的点并画出函数图象; (3)、通过观察函数图象,小明发现该函数图象与反比例函数y = (k>0)的图象形状相同,是轴对称图形,请直接写出该函数图象的对称轴的表达式:;(4)、当-2≤ x≤ 时,关于x的方程kx+ 3= 有实数解,求k的取值范围.
(3)、通过观察函数图象,小明发现该函数图象与反比例函数y = (k>0)的图象形状相同,是轴对称图形,请直接写出该函数图象的对称轴的表达式:;(4)、当-2≤ x≤ 时,关于x的方程kx+ 3= 有实数解,求k的取值范围. -
24. 抛物线 (a<0,h>0)的图象与x轴相交于A,B两点(A在B的左侧),与y轴相交于点P,顶点为C,以AB为直径的圆恰过顶点C且与y轴的正半轴相交于点Q,
 (1)、求点A的坐标,并用h的代数式表示a;(2)、当点P是OQ的中点时,求直径AB的长;(3)、如图直线AM垂直AC交抛物线于点M,点T的坐标是(6,0),当以点A,T,C为顶点的三角形与△ABM相似时,求h的值。
(1)、求点A的坐标,并用h的代数式表示a;(2)、当点P是OQ的中点时,求直径AB的长;(3)、如图直线AM垂直AC交抛物线于点M,点T的坐标是(6,0),当以点A,T,C为顶点的三角形与△ABM相似时,求h的值。
