浙江省宁波市七中教育集团2021-2022学年九年级下学期数学第三次月考试题卷

试卷更新日期：2022-04-06 类型：月考试卷

进入出卷网下载

一、选择题：（每小题4分，共40分。在每小题给出的四个选项中，只有一项符合题目要求）

1. $- \frac{7}{2}$ 的相反数是（）

A、 $- \frac{7}{2}$ B、 $- \frac{2}{7}$ C、 $\frac{2}{7}$ D、 $\frac{7}{2}$

查看试题解析
2. 据央视网消息，全国广大共产党员积极响应党中央号召，踊跃捐款，表达对新冠肺炎疫情防控工作的支持，据统计，截至3月20日，全国已有7901万多名党员自愿捐款，共捐款82.6亿元，82.6亿用科学记数法可表示为（）

A、0.826×10¹⁰ B、8.26×10⁹ C、8.26×10⁸ D、82.6×10⁸

查看试题解析
3. 一个几何体由大小相同的小立方块搭成，它的俯视图如图所示，其中小正方形中的数字表示在该位置小立方块的个数，则该几何体的主视图为（）

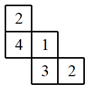A、 B、 C、 D、

查看试题解析
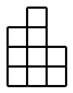4. 下列计算正确的是（）

A、a²·a³=a⁶ B、a⁶^÷a^-2=a^-3 C、（-2ab²）³=-8a³b⁶ D、（2a+b）²=4a²+b²

查看试题解析
5. 泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的（）

A、图形的平移 B、图形的旋转 C、图形的轴对称 D、图形的相似

查看试题解析
6. 如图，数轴上两点M，N所对应的实数分别为m，n，则m-n的结果可能是（）

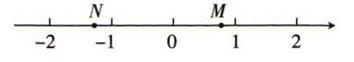A、-1 B、1 C、2 D、3

查看试题解析
7. 某厂计划加工180万个医用口罩，第一周按原计划的速度生产，一周后以原来速度的1.5倍生产，结果比原计划提前一周完成任务若设原计划每周生产x万个口罩，则可列方程为（）

A、 $\frac{180 - x}{x} = \frac{180 - x}{1.5 x} + 1$ B、 $\frac{180 - x}{x} = \frac{180 - x}{1.5 x} - 1$ C、 $\frac{180}{x} = \frac{180}{1.5 x} + 2$ D、 $\frac{180}{x} = \frac{180}{1.5 x} - 2$

查看试题解析
8. 如图，菱形ABCD的边长为10，面积为80，∠BAD<90°，⊙O与边AB，AD都相切，菱形的顶点A到圆心O的距离为5，则⊙O的半径长等于（）

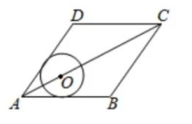A、2.5 B、 $\sqrt{5}$ C、2 $\sqrt{2}$ D、3

查看试题解析
9. 如图1，正方形ABCD中，AC，BD相交于点O，E是OD的中点，动点P从点E出发，沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A，在此过程中线段AP的长度y随着运动时间x的函数关系如图2所示，则AB的长为（）

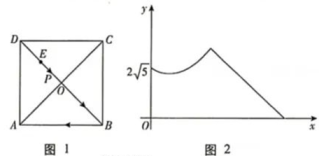A、4 $\sqrt{2}$ B、4 C、3 $\sqrt{3}$ D、2 $\sqrt{2}$

查看试题解析
10. 勾股定理是人类最伟大的科学发现之一。如图1，分别以直角三角形的各边为边向外作三个等边三角形：如图2，将较小的两个等边三角形△AFG和△BDE放在最大的等边三角形△ABC内，DE与FG交于点P，连结AP，FE．欲求△GEC的面积，只需知道下列哪个三角形的面积即可（）

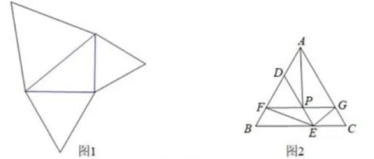A、△APG B、△ADP C、△DFP D、△FEG

查看试题解析

二、填空题：（每小题5分，共30分）

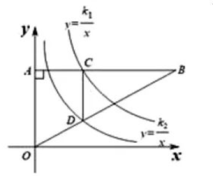
11. 分解因式： xy²4x=

查看试题解析
12. 一个不透明的袋子里装有除颜色不同其他都相同的红球、黄球和蓝球，其中红球有2个，黄球有1个，从中任意摸出1球是红球的概率为 $\frac{1}{4}$ ，则蓝球的个数是

查看试题解析
13. 一个圆锥的底面半径r=10，高h=20，则这个圆锥的侧面积是

查看试题解析
14. 已知关于x的一元二次方程x²-4x-2k+8=0有两个实数根x₁ ， x₂ ，若x₁³x₂+x₁x₂³=24，则k的值是

查看试题解析
15. 如图，在平面直角坐标系中，Rt△AOB的直角边OA在y轴的正半轴上，反比例函数y= $\frac{k_{1}}{x}$ 的图像交直角边AB于点C，反比例函数y= $\frac{k_{2}}{x}$ 的图像交斜边OB于点D，CD∥y轴，S_△B_CD=3k₁-7.5k₂ ，则 $\frac{k_{1}}{k_{2}}$ 的值是

查看试题解析
16. 如图，半径为2，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P向半径OA引垂线PH，交OA于点H，设△OPH的内心为I，当点P在弧AB．上从点A运动到点B时，线段BI的最小值为

查看试题解析

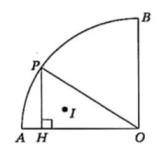
三、解答题：（本大题有 8小题，第17~20小题每小题8分，第21小题10分，第22、23小题每小题12分，第24小题14分，共80分）

17.

(1)、计算： ${(- \frac{1}{2})}^{- 1} + | - 2 | + 4 s i n 60 ° - \sqrt{12} + (π - 3)^{0}$

(2)、先化简，再求值： $1 - \frac{a - b}{a + 2 b} \div \frac{a^{2} - b^{2}}{a^{2} + 4 a b + 4 b^{2}}$ ，其中a= $\sqrt{3}$ -3，b=3．

查看试题解析
18. 某中学为了解九年级学生对新冠肺炎防控知识的掌握情况，从全校九年级学生中随机抽取部分学生进行调查．调查结果分为四类： A类——非常了解： B类——比较了解； C类——一般了解： D类-不了解．现将调查结果绘制成如下不完整的统计图，请根据统计图中的信息解答下列问题：

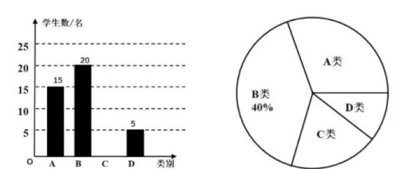(1)、本次共调查了名学生；

(2)、补全条形统计图．

(3)、 D类所对应扇形的圆心角的大小为；

(4)、若该校九年级学生共有500名，根据以上抽样结果，估计该校九年级学生对新冠肺炎防控知识非常了解的约有多少名？

查看试题解析
19. 如图，在4x4的方格子中，△ABC的三个顶点都在格点上．

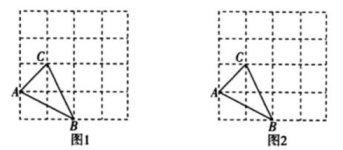(1)、在图1中画出线段CD，使CD⊥CB，其中D是格点．

(2)、在图2中画出平行四边形ABEC，其中E是格点．

查看试题解析
20. 宁波市某校数学兴趣小组借助无人机测量一条河流的宽度CD．如图所示，一架水平飞行的无人机在A处测得正前方河流的左岸C处的俯角为α，无人机沿水平线AF方向继续飞行50米至B处，测得正前方河流右岸D处的俯角为30°．线段AM的长为无人机距地面的铅直高度，点M、C、D在同一条直线上．其中tanα=2， MC= 50 $\sqrt{3}$ 米．

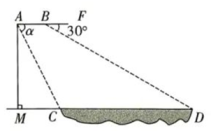(1)、求无人机的飞行高度AM；（结果保留根号）

(2)、求河流的宽度CD．（结果精确到1米，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
21. 一辆快车从宁波开往北京，一辆慢车从北京开往宁波，两车同时出发，分别以各自的速度在宁波和北京两地间匀速行驶1h后，快车司机发现有重要文件遗忘在宁波，便立即返回拿上文件（取文件时间不计）后再从宁波开往北京，结果快车先到达北京，慢车继续行驶到宁波．设慢车行驶时间为x（h），两车之间的距离为y（km），y与x的函数图象如图所示，请回答下列问题：

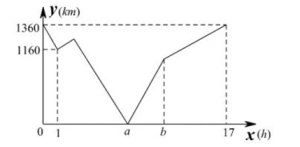(1)、直接写出宁波与北京的距离．

(2)、求快车的速度．

(3)、求a的值，并说明a所表示的实际意义．

(4)、求b的值，并说明b所表示的实际意义．

查看试题解析
22. 如图，已知四边形ABCD是矩形，点E在BA的延长线上，AE=AD，EC与BD相交于点G，与AD相交于点F，AF=AB．

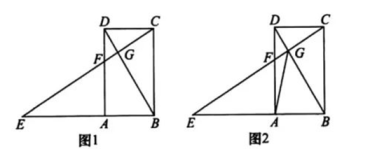(1)、求证： BD⊥EC：

(2)、若AB=1，求AE的长；

(3)、如图2，连接AG，求证： EG- DG= $\sqrt{2}$ AG．

查看试题解析
23. 如图，已知抛物线y=-x²+bx+3的图象与x轴相交于点A和点B，与y轴交于点C，图象的对称轴为直线x=-1．连结AC，有一动点D在线段AC上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F．设点D的横坐标为m．

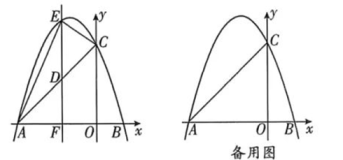(1)、求AB的长度；

(2)、连结AE、CE，当△ACE的面积最大时，求点D的坐标：

(3)、直接写出m为何值时，△ADF与△CDE相似．

查看试题解析
24. 在圆O中，AO、BO、是圆O的半径，点C在劣弧AB上，OA=10，AC=12，AC∥OB，连结AB ．

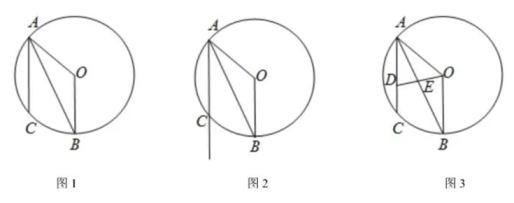(1)、如图1，求证：AB平分∠OAC；

(2)、点M在弦AC的延长线上，连结BM，如果△AMB是直角三角形，请你在图2中画出点M的位置并求CM的长：

(3)、如图，点D在弦AC上，与点A不重合，连结OD与弦AB交于点E，设点D与点C的距离为x，△OEB的面积为y，求y与x的函数关系式，并写出自变量x的取值范围．

查看试题解析

浙江省宁波市七中教育集团2021-2022学年九年级下学期数学第三次月考试题卷

一、选择题：（每小题4分，共40分。在每小题给出的四个选项中，只有一项符合题目要求）

二、填空题： （每小题5分，共30分）

三、解答题： （本大题有 8小题，第17~20小题每小题8分，第21小题10分，第22、23小题每小题12分，第24小题14分，共80分）

二、填空题：（每小题5分，共30分）

三、解答题：（本大题有 8小题，第17~20小题每小题8分，第21小题10分，第22、23小题每小题12分，第24小题14分，共80分）