安徽省安庆市2021-2022学年九年级下学期综合素质调研数学试卷
试卷更新日期:2022-04-06 类型:开学考试
一、单选题
-
1. 下列二次函数中,对称轴为直线x = 1的是( )A、y=-x2+1 B、y= (x–1) 2 C、y= (x+1) 2 D、y =-x2-12. 若 , 则的值为( )A、 B、 C、 D、3. 在中, , , 则的值为( )A、 B、 C、 D、4. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、5. 如图,在▱ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,他们相交于G,延长BE交CD的延长线于点H,则图中的相似三角形共有( )
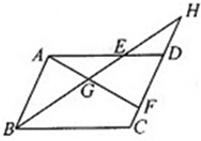 A、2对 B、3对 C、4对 D、5对6. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )
A、2对 B、3对 C、4对 D、5对6. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )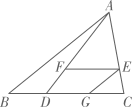 A、 B、 C、 D、7. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、
A、 B、 C、 D、7. 某气球内充满了一定质量 的气体,当温度不变时,气球内气体的气压 (单位: )是气体体积 (单位: )的反比例函数: ,能够反映两个变量 和 函数关系的图象是( )A、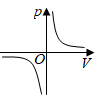 B、
B、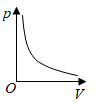 C、
C、 D、
D、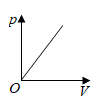 8. 已知如图: , 且 , 则的大小是( )
8. 已知如图: , 且 , 则的大小是( )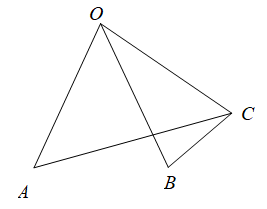 A、45° B、50° C、55° D、65°9. 如图,在中, , , D、E在斜边AB边上, , 若 , 则的面积为( )
A、45° B、50° C、55° D、65°9. 如图,在中, , , D、E在斜边AB边上, , 若 , 则的面积为( )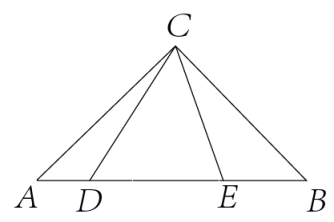 A、6 B、 C、4 D、10. 如图,坐标系的原点为O,点P是第一象限内抛物线y= x2﹣1上的任意一点,PA⊥x轴于点A.则OP﹣PA值为( )
A、6 B、 C、4 D、10. 如图,坐标系的原点为O,点P是第一象限内抛物线y= x2﹣1上的任意一点,PA⊥x轴于点A.则OP﹣PA值为( )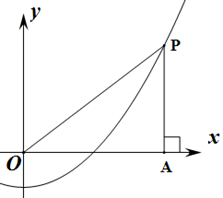 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
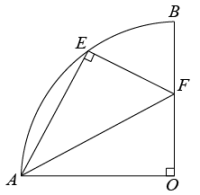
11. 抛物线的顶点在x轴上,那么.12. 反比例函数图象与正比例函数图象交于 , , 则的值为.13. 如图,在扇形AOB中, , 点E在弧AB上,点F在OB上, , 若 , , 则扇形AOB半径为.
 14. 如图.直线与坐标轴相交于A、B两点,动点P在线段AB上,动点Q在线段OA上、连结OP,且满足 , 则当度时,线段OQ的最小值为.
14. 如图.直线与坐标轴相交于A、B两点,动点P在线段AB上,动点Q在线段OA上、连结OP,且满足 , 则当度时,线段OQ的最小值为.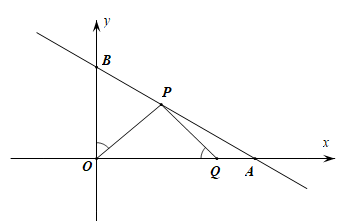
三、解答题
-
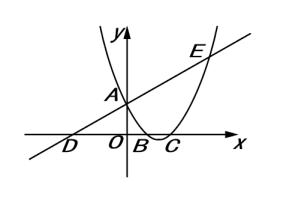
15. 计算:.16. 如图,已知直钱与y轴交于点A,与x轴交于点D,抛物线与直线交于A,E两点,与x轴交于B,C两点,点B的坐标为 , 求该抛物线对应的函数表达式.
 17. 如图,一次函数y=-x+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B两点.
17. 如图,一次函数y=-x+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B两点.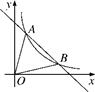 (1)、求反比例函数的解析式;(2)、在第一象限内,当一次函数y=-x+5的值大于反比例函数y= (k≠0)的值时,写出自变量x的取值范围.18. 如图,在正方形 中, 为边 的中点,点 在边 上,且 ,延长 交 的延长线于点 .
(1)、求反比例函数的解析式;(2)、在第一象限内,当一次函数y=-x+5的值大于反比例函数y= (k≠0)的值时,写出自变量x的取值范围.18. 如图,在正方形 中, 为边 的中点,点 在边 上,且 ,延长 交 的延长线于点 .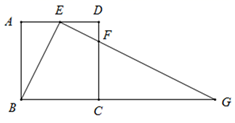 (1)、求证:△ ∽△ .(2)、若 ,求 的长.19. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)
(1)、求证:△ ∽△ .(2)、若 ,求 的长.19. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)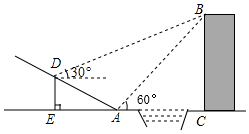 20. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , , .
20. 如图,在平面直角坐标系中,已知的三个顶点坐标分别是 , , .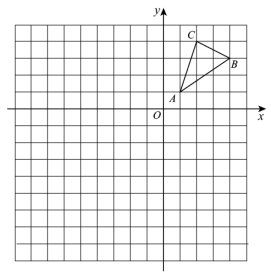 (1)、请作出绕O点逆时针旋转90°的 , 并求出线段AB扫过的面积.(2)、以点O为位似中心,将扩大为原来的2倍,得到 , 在y轴的左侧.21. 如图,AB是的弦,点C是在过点B的切线上,且且交AB于点P.
(1)、请作出绕O点逆时针旋转90°的 , 并求出线段AB扫过的面积.(2)、以点O为位似中心,将扩大为原来的2倍,得到 , 在y轴的左侧.21. 如图,AB是的弦,点C是在过点B的切线上,且且交AB于点P.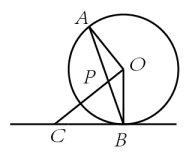 (1)、求证:(2)、若的半径为 , 求证:为等边三角形.
(1)、求证:(2)、若的半径为 , 求证:为等边三角形.