山东省济宁市任城区2020-2021学年高二下学期数学期中考试试卷
试卷更新日期:2022-04-06 类型:期中考试
一、单选题
-
1. 函数 的图象如图所示,则下列数值排序正确的是( )
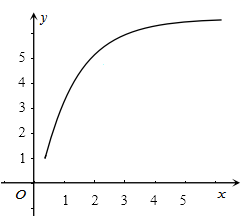 A、 B、 C、 D、2. 将6本相同的书分给8个同学,每人至多分一本,而且书必须分完,则不同的分法种数是( )A、 B、 C、 D、3. 习近平总书记在“十九大”报告中指出:坚定文化自信,推动中华优秀传统文化创造性转化.“杨辉三角”揭示了二项式系数在三角形中的一种几何排列规律,最早在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现,欧洲数学家帕斯卡在1654年才发现这一规律,比杨辉要晚近四百年.“杨辉三角”是中国数学史上的一个伟大成就,激发起一批又一批数学爱好者的探究欲望.如图所示,在由二项式系数所构成的“杨辉三角”中,第10行第9个数是( )
A、 B、 C、 D、2. 将6本相同的书分给8个同学,每人至多分一本,而且书必须分完,则不同的分法种数是( )A、 B、 C、 D、3. 习近平总书记在“十九大”报告中指出:坚定文化自信,推动中华优秀传统文化创造性转化.“杨辉三角”揭示了二项式系数在三角形中的一种几何排列规律,最早在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现,欧洲数学家帕斯卡在1654年才发现这一规律,比杨辉要晚近四百年.“杨辉三角”是中国数学史上的一个伟大成就,激发起一批又一批数学爱好者的探究欲望.如图所示,在由二项式系数所构成的“杨辉三角”中,第10行第9个数是( )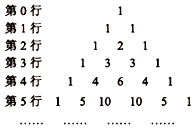 A、9 B、10 C、36 D、454. 已知随机变量的分布列为 , , 2,3,4,则( )A、 B、 C、4 D、55. 今天是星期二,经过7天后还是星期二,那么经过天后是( )A、星期一 B、星期二 C、星期三 D、星期四6. 在的展开式中,的系数为( )A、-80 B、80 C、160 D、2407. 函数的图象大致是( )A、
A、9 B、10 C、36 D、454. 已知随机变量的分布列为 , , 2,3,4,则( )A、 B、 C、4 D、55. 今天是星期二,经过7天后还是星期二,那么经过天后是( )A、星期一 B、星期二 C、星期三 D、星期四6. 在的展开式中,的系数为( )A、-80 B、80 C、160 D、2407. 函数的图象大致是( )A、 B、
B、 C、
C、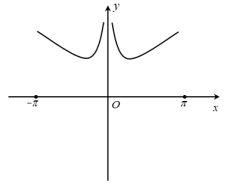 D、
D、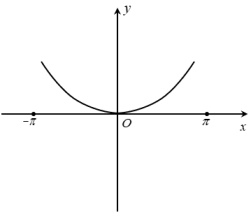 8. 已知函数的定义域为R,且 , , 则不等式的解集为( )A、 B、 C、 D、
8. 已知函数的定义域为R,且 , , 则不等式的解集为( )A、 B、 C、 D、二、多选题
-
9. 下列导数运算正确的是( )A、 B、 C、 D、10. 已知函数的导函数是 , 的图象如图所示,下列说法正确的是( )
 A、函数在上单调递减 B、函数在上单调递减 C、函数在处取得极大值 D、函数共有2个极小值点11. 从1,2,3,4,5,6中任取三个不同的数组成一个三位数,则在所组成的数中( )A、偶数有60个 B、比300大的奇数有48个 C、个位和百位数字之和为7的数有24个 D、能被3整除的数有48个12. 已知 , 为自然对数的底数,则下列不等式一定成立的是( )A、 B、 C、 D、
A、函数在上单调递减 B、函数在上单调递减 C、函数在处取得极大值 D、函数共有2个极小值点11. 从1,2,3,4,5,6中任取三个不同的数组成一个三位数,则在所组成的数中( )A、偶数有60个 B、比300大的奇数有48个 C、个位和百位数字之和为7的数有24个 D、能被3整除的数有48个12. 已知 , 为自然对数的底数,则下列不等式一定成立的是( )A、 B、 C、 D、三、填空题
-
13. 若 , 则n!= .14. 若函数满足 , 则 .15. 甲和乙两个箱子里各装有6个球,其中甲箱中有3个红球、3个白球,乙箱中有4个红球、2个白球.掷一枚质地均匀的骰子,如果点数不超过2,从甲箱子中摸出1个球;如果点数超过2,从乙箱子中摸出1个球,则摸到红球的概率为 .16. 若 , 则 , .
四、解答题
-
17. 已知函数 .(1)、当时,求的单调区间;(2)、若在区间上单调递增,求的取值范围.18. 在下面三个条件中任选一个,补充在下面的问题中,并对其求解.
条件①:第3项与第7项的二项式系数相等;
条件②:只有第5项的二项式系数最大;
条件③:所有项的二项式系数的和为256.
问题:在的展开式中,____.
(1)、求的值;(2)、若其展开式中的常数项为112,求其展开式中所有项的系数的和.19. 某礼品店要制作一批长方体包装盒,材料是边长为 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是 的正方形,然后在余下两个角处各切去一个长、宽分别为 、 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒. (1)、求包装盒的容积 关于 的函数表达式,并求函数的定义域;(2)、当 为多少时,包装盒的容积最大?最大容积是多少?
(1)、求包装盒的容积 关于 的函数表达式,并求函数的定义域;(2)、当 为多少时,包装盒的容积最大?最大容积是多少?