江苏省淮安市金湖、洪泽等六校2020-2021学年高二下学期数学期中考试试卷
试卷更新日期:2022-04-06 类型:期中考试
一、单选题
-
1. 复数 , 则在复平面内, 对应的点的坐标是( )A、 B、 C、 D、2. 曲线在处的切线如图所示,则( )
 A、0 B、-1 C、1 D、3. 在的展开式中x的系数为( )A、80 B、240 C、-80 D、1604. 为响应国家精准扶贫政策,某工作组要在村外一湖岸边修建一段道路(如图中虚线处),要求该道路与两条直线道路平滑连接(注:两直线道路:y1= 2x,y2=3x 6分别与该曲线相切于(0,0),(2,0),已知该弯曲路段为三次函数图象的一部分,则该函数解析式为( )
A、0 B、-1 C、1 D、3. 在的展开式中x的系数为( )A、80 B、240 C、-80 D、1604. 为响应国家精准扶贫政策,某工作组要在村外一湖岸边修建一段道路(如图中虚线处),要求该道路与两条直线道路平滑连接(注:两直线道路:y1= 2x,y2=3x 6分别与该曲线相切于(0,0),(2,0),已知该弯曲路段为三次函数图象的一部分,则该函数解析式为( ) A、 B、 C、 D、5. 要从甲、乙等7人中选4人在座谈会上发言,若甲、乙都被选中,且他们发言中间恰好间隔一人,那么不同的发言顺序共有( )A、80种 B、120种 C、60种 D、240种6. 已知函数 的图象如图所示,则其导函数的图象大致形状为( )
A、 B、 C、 D、5. 要从甲、乙等7人中选4人在座谈会上发言,若甲、乙都被选中,且他们发言中间恰好间隔一人,那么不同的发言顺序共有( )A、80种 B、120种 C、60种 D、240种6. 已知函数 的图象如图所示,则其导函数的图象大致形状为( )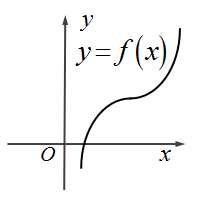 A、
A、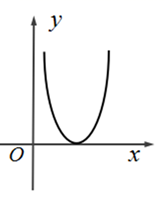 B、
B、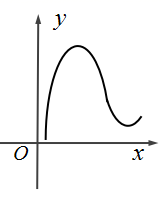 C、
C、 D、
D、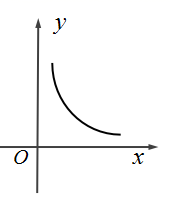 7. 设复数(i是虚数单位),则( )A、-2 B、-i C、2 D、08. 1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式 , 这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式,有下列四个结论:①;②;
7. 设复数(i是虚数单位),则( )A、-2 B、-i C、2 D、08. 1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写出以下公式 , 这个公式在复变论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式,有下列四个结论:①;②;③;④.其中所有正确结论的编号是( )
A、①②③ B、②④ C、①②④ D、①③二、多选题
-
9. 我国南宋数学家杨辉1261年所著的《详解九章算法》就给出了著名的杨辉三角,由此可见我国古代数学的成就是非常值得中华民族自豪的.以下关于杨辉三角的猜想中正确的有( )
 A、由“在相邻的两行中,除1以外的每一个数都等于它‘肩上’两个数的和”猜想: B、 C、第34行中从左到右第14与第15个数的比为 D、由“第n行所有数之和为”猜想:10. 甲,乙,丙,丁,戊五人并排站成一排照相,下列说法正确的是( )A、如果甲,乙必须相邻,那么不同的排法有24种 B、甲不站在排头,乙不站在正中间,则不同的排法共有78种 C、甲乙不相邻且乙在甲的右边,则不同的排法共有36种 D、若五人已站好,后来情况有变,需加上2人,但不能改变原来五人的相对顺序,则不同的排法共有42种11. 定义在区间上的连续函数的导函数为 , 若使得 , 则称为区间上的“中值点”.下列在区间上“中值点”多于一个的函数是( )A、 B、 C、 D、12. 在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer),简单的讲就是对于满足一定条件的连续函数 , 存在一个点 , 使得 , 那么我们称该函数为“不动点”函数,而称为该函数的一个不动点.依据不动点理论,下列说法正确的是( )A、函数有1个不动点 B、函数有2个不动点 C、若定义在R上的奇函数 , 其图像上存在有限个不动点,则不动点个数是奇数 D、若函数在区间上存在不动点,则实数a满足(e为自然对数的底数)
A、由“在相邻的两行中,除1以外的每一个数都等于它‘肩上’两个数的和”猜想: B、 C、第34行中从左到右第14与第15个数的比为 D、由“第n行所有数之和为”猜想:10. 甲,乙,丙,丁,戊五人并排站成一排照相,下列说法正确的是( )A、如果甲,乙必须相邻,那么不同的排法有24种 B、甲不站在排头,乙不站在正中间,则不同的排法共有78种 C、甲乙不相邻且乙在甲的右边,则不同的排法共有36种 D、若五人已站好,后来情况有变,需加上2人,但不能改变原来五人的相对顺序,则不同的排法共有42种11. 定义在区间上的连续函数的导函数为 , 若使得 , 则称为区间上的“中值点”.下列在区间上“中值点”多于一个的函数是( )A、 B、 C、 D、12. 在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer),简单的讲就是对于满足一定条件的连续函数 , 存在一个点 , 使得 , 那么我们称该函数为“不动点”函数,而称为该函数的一个不动点.依据不动点理论,下列说法正确的是( )A、函数有1个不动点 B、函数有2个不动点 C、若定义在R上的奇函数 , 其图像上存在有限个不动点,则不动点个数是奇数 D、若函数在区间上存在不动点,则实数a满足(e为自然对数的底数)三、填空题
-
13. 设 , 且 , 若能被整除,则.14. 若函数 , 则满足不等式的的取值范围为.15. 将7名支教教师安排到3所学校任教,每校至少2人的分配方法总数为a,则二项式的展开式中含x项的系数为(用数字作答).16. 若 , , , 且对任意 , (),恒成立,则实数a的取值范围为.
四、解答题
-
17. 已知复数(),且是纯虚数.(1)、求复数z及;(2)、在复平面内,若复数()对应点在第二象限,求实数m的取值范围.18. 在①的一个极值点为0,②为奇函数,③若曲线在点处的切线与直线垂直这三个条件中任选一个,补充在下面的问题中,并回答下列问题.
已知函数 , 且_________,求在上的最大值与最小值.
注:如果选择多个条件解答,按第一个解答计分.
19. 已知的展开式中 ,(1)、求;(2)、展开式中系数最大的项为第几项?(3)、求(注: , )20. 已知函数 , .(1)、若函数在上是增函数,求实数a的取值范围;(2)、若函数在上的最小值为2,求实数a的值.21. 六安市某生态旅游景区升级改造,有一块半圆形土地打算种植花草供人游玩欣赏,如图所示,其中AB长为km,C、D两点在半圆弧上,满足 , 设. (1)、现要在景区内铺设一条观光道路,由线段BC,CD和组成,则当为何值时,观光道路的总长最长,并求最大值;(2)、若在和内种满月季花,在扇形内种满薰衣草,已知月季花利润是每平方千米元,薰衣草的利润是每平方千米元,则当为何值时,才能使总利润最大?最大利润是多少?22. 已知函数 , (为常数).(1)、若函数与函数在处有相同的切线,求实数的值;(2)、若 , 且 , 证明:;(3)、若对任意 , 不等式恒成立,求实数的取值范围.
(1)、现要在景区内铺设一条观光道路,由线段BC,CD和组成,则当为何值时,观光道路的总长最长,并求最大值;(2)、若在和内种满月季花,在扇形内种满薰衣草,已知月季花利润是每平方千米元,薰衣草的利润是每平方千米元,则当为何值时,才能使总利润最大?最大利润是多少?22. 已知函数 , (为常数).(1)、若函数与函数在处有相同的切线,求实数的值;(2)、若 , 且 , 证明:;(3)、若对任意 , 不等式恒成立,求实数的取值范围.