2022年中考数学二轮专题复习-三角形及全等
试卷更新日期:2022-04-05 类型:二轮复习
一、单选题
-
1. 以下列各组长度的线段为边,能构成三角形的是( )A、7 、5、12 B、6、8、15 C、8、4、3 D、4、6、52. 在下列图形中,线段 AD 的长表示点 A 到直线 BC 的距离的是( )A、
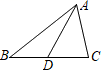 B、
B、 C、
C、 D、
D、 3. 尺规作图:作 角等于已知角 .示意图如图所示,则说明 的依据是( )
3. 尺规作图:作 角等于已知角 .示意图如图所示,则说明 的依据是( )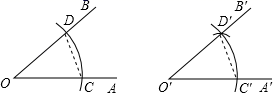 A、SSS B、SAS C、ASA D、AAS4. 人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A、SSS B、SAS C、ASA D、AAS4. 人字梯中间一般会设计一“拉杆”,这样做的道理是( )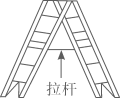 A、两点之间线段最短 B、三角形的稳定性 C、两点确定一条直线 D、垂线段最短5. 在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )A、1个 B、2个 C、3个 D、4个6. 如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有( )
A、两点之间线段最短 B、三角形的稳定性 C、两点确定一条直线 D、垂线段最短5. 在平面直角坐标系xOy中,点A(﹣2,0),点B(0,3),点C在坐标轴上,若三角形ABC的面积为6,则符合题意的点C有( )A、1个 B、2个 C、3个 D、4个6. 如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有( )①△BPQ是等边三角形;②△PCQ是直角三角形;③∠APB=150°;④∠APC=120°.
 A、①②③ B、①②④ C、②③④ D、①②③④7. 如图,已知点D,E,F分别在△ABC的三边上,将△ABC沿DE,DF翻折,顶点B,C均落在△ABC内的点O处,且BD与CD重合于线段OD,若∠AEO+∠AFO=58°,则∠A的度数为( )
A、①②③ B、①②④ C、②③④ D、①②③④7. 如图,已知点D,E,F分别在△ABC的三边上,将△ABC沿DE,DF翻折,顶点B,C均落在△ABC内的点O处,且BD与CD重合于线段OD,若∠AEO+∠AFO=58°,则∠A的度数为( )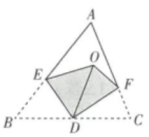 A、58° B、59° C、60° D、61°8. 如图所示,在四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A、58° B、59° C、60° D、61°8. 如图所示,在四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( ) A、4个 B、3个 C、2个 D、1个9. 在测量一个小口圆柱形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,CD为直径,测得AB=a,EF=b,则圆柱形容器的壁厚是( )
A、4个 B、3个 C、2个 D、1个9. 在测量一个小口圆柱形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,CD为直径,测得AB=a,EF=b,则圆柱形容器的壁厚是( ) A、a B、b C、b-a D、(b-a)10. 如图,在 中, , , 为 边的中点, , 绕 点旋转,它的两边分别交 和 的延长线于 , ,当点 在 延长线上时, , , 的关系为( )
A、a B、b C、b-a D、(b-a)10. 如图,在 中, , , 为 边的中点, , 绕 点旋转,它的两边分别交 和 的延长线于 , ,当点 在 延长线上时, , , 的关系为( ) A、 = B、 = C、 = D、 =11. 如图, , ,欲证 ,则可增加的条件是( )
A、 = B、 = C、 = D、 =11. 如图, , ,欲证 ,则可增加的条件是( ) A、 B、 C、 D、12. 如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
A、 B、 C、 D、12. 如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( ) A、 B、 C、 D、13. 如图,已知平行四边形ABCD的面积为100,P为边CD上的任意一点,E,F分别是线段PA,PB的中点,则图中阴影部分的总面积为( )
A、 B、 C、 D、13. 如图,已知平行四边形ABCD的面积为100,P为边CD上的任意一点,E,F分别是线段PA,PB的中点,则图中阴影部分的总面积为( ) A、30 B、25 C、22.5 D、5014. 如图, 中, , ,D、E为BC边上两点, ,过A点作 ,且 ,连接DF、BF.下列结论:① ,②AD平分 ;③若 , ,则 ;④若 , ,其中正确的个数有( )
A、30 B、25 C、22.5 D、5014. 如图, 中, , ,D、E为BC边上两点, ,过A点作 ,且 ,连接DF、BF.下列结论:① ,②AD平分 ;③若 , ,则 ;④若 , ,其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个15. 如图,在△ABC中,∠ABC=45°,AB=3,AD⊥BC于点D,BE⊥AC于点E,AE=1.连接DE,将△AED沿直线AE翻折至△ABC所在的平面内,得△AEF,连接DF.过点D作DG⊥DE交BE于点G.则下列结论正确的有( )个.
A、1个 B、2个 C、3个 D、4个15. 如图,在△ABC中,∠ABC=45°,AB=3,AD⊥BC于点D,BE⊥AC于点E,AE=1.连接DE,将△AED沿直线AE翻折至△ABC所在的平面内,得△AEF,连接DF.过点D作DG⊥DE交BE于点G.则下列结论正确的有( )个.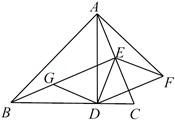
①△BDG≌△ADE;②△GDE为等腰直角三角形;③四边形DFEG的周长为2 +2.
A、3 B、2 C、1 D、016. 如图,边长为5的等边三角形 中,M是高 所在直线上的一个动点,连接 ,将线段 绕点B逆时针旋转 得到 ,连接 .则在点M运动过程中,线段 长度的最小值是( ) A、 B、1 C、2 D、17. 将△OBA按如图方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为 , 将△OAB绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点A对应点的坐标为( )
A、 B、1 C、2 D、17. 将△OBA按如图方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为 , 将△OAB绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点A对应点的坐标为( )
 A、 B、 C、 D、18. 如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD , AE相交于F , 已知BD=4AD , 设△ABC的面积为S , △CEF的面积为S1 , △ADF的面积为S2 , 则 的值为( )
A、 B、 C、 D、18. 如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD , AE相交于F , 已知BD=4AD , 设△ABC的面积为S , △CEF的面积为S1 , △ADF的面积为S2 , 则 的值为( )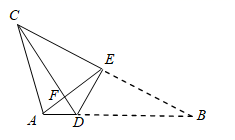 A、 B、 C、 D、19. 在平行四边形 中, , 于E, 于F, , BF相交于H , BF与AD的延长线相交于点G , 下面给出四个结论:① ;② ;③ ;④ ,其中正确的结论是( )
A、 B、 C、 D、19. 在平行四边形 中, , 于E, 于F, , BF相交于H , BF与AD的延长线相交于点G , 下面给出四个结论:① ;② ;③ ;④ ,其中正确的结论是( )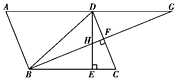 A、②③ B、①②④ C、②③④ D、①②③④20. 如图,在平面直角坐标系中,平行四边形 的边 在y轴的正半轴上,反比例函数 的图象分别交 于中点D,交 于点E,且 ,连接 ,若 ,则k的值为( )
A、②③ B、①②④ C、②③④ D、①②③④20. 如图,在平面直角坐标系中,平行四边形 的边 在y轴的正半轴上,反比例函数 的图象分别交 于中点D,交 于点E,且 ,连接 ,若 ,则k的值为( ) A、5 B、 C、6 D、
A、5 B、 C、6 D、二、填空题
-
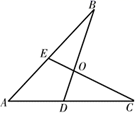
21. 如图,已知 ABD≌ ACE,∠A=53°,∠B=21°,则∠BEC=°.
 22. 用海伦公式求面积的计算方法是: ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中,已知三边之长 , , ,则 的面积为.23. 如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为
22. 用海伦公式求面积的计算方法是: ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中,已知三边之长 , , ,则 的面积为.23. 如图,在△ABC中,AB=AC,D为BC上的一点,∠BAD=28°,在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE∥AB,则∠DOC的度数为 24. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为.
24. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D.E为线段BD上一点,连结CE,将边BC沿CE折叠,使点B的对称点B'落在CD的延长线上.若AB=10,BC=8,则△ACE的面积为. 25. 如图,把一副三角板按如图放置,∠ACB=∠ADB=90°,∠CAB=30°,∠DAB=45°,点E是AB的中点,连结CE,DE,DC.若AB=6,则∆DEC的面积为
25. 如图,把一副三角板按如图放置,∠ACB=∠ADB=90°,∠CAB=30°,∠DAB=45°,点E是AB的中点,连结CE,DE,DC.若AB=6,则∆DEC的面积为 26. 在 ABC中,AD⊥BC于点D,BD=CD,若BC=6,AD=4,则图中阴影部分的面积为.
26. 在 ABC中,AD⊥BC于点D,BD=CD,若BC=6,AD=4,则图中阴影部分的面积为. 27. 如图,在△ABC中, AB=AC ,BC=3+ ,∠BAC=90°,点D、E都在边BC上,∠DAE=45°.若BD=2CE,则DE的长是。
27. 如图,在△ABC中, AB=AC ,BC=3+ ,∠BAC=90°,点D、E都在边BC上,∠DAE=45°.若BD=2CE,则DE的长是。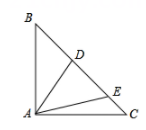 28. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.
28. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.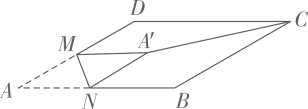 29. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF.其中正确的有.
29. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF.其中正确的有.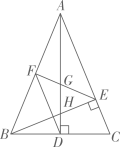 30. 如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC',DC'与AB交于点E,连接AC',若AD=AC'=2,BD=3,则点D到BC的距离为.
30. 如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC',DC'与AB交于点E,连接AC',若AD=AC'=2,BD=3,则点D到BC的距离为.
三、作图题
-
31. 如图所示,在平面直角坐标系中 的三个顶点坐标分别为 , , .
 (1)、作出 关于x轴对称的 ;(2)、 的面积为 , 边上的高为;(3)、在y轴找一点P,使得 的周长最小,请画出点P,并直接写出 的周长最小值为;(4)、在x轴上找一点P,使得 为等腰三角形,则点P的坐标为 .32. 如图,在所给平面直角坐标系(每小格均为边长是1个单位长度的正方形)中完成下列各题.
(1)、作出 关于x轴对称的 ;(2)、 的面积为 , 边上的高为;(3)、在y轴找一点P,使得 的周长最小,请画出点P,并直接写出 的周长最小值为;(4)、在x轴上找一点P,使得 为等腰三角形,则点P的坐标为 .32. 如图,在所给平面直角坐标系(每小格均为边长是1个单位长度的正方形)中完成下列各题. (1)、已知 , , ,画出 关于 轴对称的图形△ ,并写出 的坐标;(2)、在 轴上画出点 ,使 最小;(3)、在(1)的条件下,在 轴上画出点 ,使 最大.
(1)、已知 , , ,画出 关于 轴对称的图形△ ,并写出 的坐标;(2)、在 轴上画出点 ,使 最小;(3)、在(1)的条件下,在 轴上画出点 ,使 最大.四、解答题
-
33. 如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
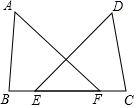 34. 如图,已知 地在 地的正东方向,两地相距 两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距变相等.上午8:00测得一辆在高速公路上行驶的汽车位于 地的正南方向 处,至上午8:20,发现该车在 地的西北方向 处,该段高速公路限速为110km/h,判断该车是否超速行驶.
34. 如图,已知 地在 地的正东方向,两地相距 两地之间有一条东北走向的高速公路,且A,B两地到这条高速公路的距变相等.上午8:00测得一辆在高速公路上行驶的汽车位于 地的正南方向 处,至上午8:20,发现该车在 地的西北方向 处,该段高速公路限速为110km/h,判断该车是否超速行驶. 35. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
35. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .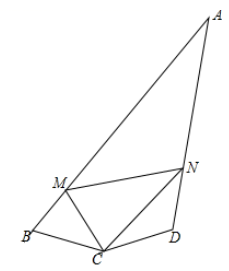 36. 如图,在 中,∠BAC=90°,AB=AC , ∠ABC的平分线交AC于点D , 过点C作BD的垂线交BD的延长线于点E , 交BA的延长线于点F . 求证:BD=2CE .
36. 如图,在 中,∠BAC=90°,AB=AC , ∠ABC的平分线交AC于点D , 过点C作BD的垂线交BD的延长线于点E , 交BA的延长线于点F . 求证:BD=2CE . 37. 探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
37. 探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE. (1)、当∠BAD=60°时,求∠CDE的度数;(2)、当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;(3)、深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.38. 小明遇到这样一个问题
(1)、当∠BAD=60°时,求∠CDE的度数;(2)、当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;(3)、深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.38. 小明遇到这样一个问题
如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法2:如图2,作BE⊥CD,垂足为点E.
方法3:如图3,作CF⊥AB,垂足为点F.
根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.