2022年浙教版数学八年级下册期中复习专题3 几何
试卷更新日期:2022-04-04 类型:复习试卷
一、单选题(每题4分,共40分)
-
1. 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、730°2. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( )
 A、1.4 B、1.6 C、1.8 D、2.23. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( )
A、1.4 B、1.6 C、1.8 D、2.23. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( ) A、 B、 C、 D、4. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )
A、 B、 C、 D、4. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )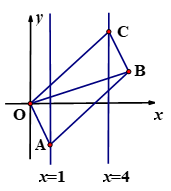 A、3 B、4 C、5 D、65. 在 中, 于 , 是 的中点, ,若 , ,则 的长是( )
A、3 B、4 C、5 D、65. 在 中, 于 , 是 的中点, ,若 , ,则 的长是( ) A、 B、 C、1 D、26. 如图,在▱ABCD中,AD=2AB , F是AD的中点,作CE⊥AB , 垂足E在线段AB上,连接EF、CF , 下列结论中:①∠DCF= ∠BCD;②∠DFE=3∠AEF;③EF=CF;④S△BEC=S△CEF . 一定成立的是( )
A、 B、 C、1 D、26. 如图,在▱ABCD中,AD=2AB , F是AD的中点,作CE⊥AB , 垂足E在线段AB上,连接EF、CF , 下列结论中:①∠DCF= ∠BCD;②∠DFE=3∠AEF;③EF=CF;④S△BEC=S△CEF . 一定成立的是( ) A、①②③④ B、①②③ C、①②④ D、①③④7. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( )
A、①②③④ B、①②③ C、①②④ D、①③④7. 如图,在平面直角坐标系中, 的顶点 在第一象限,点 的坐标分别为 、 , , ,直线 交 轴于点 ,若 与 关于点 成中心对称,则点 的坐标为( ) A、(-4,-5) B、(-5,-4) C、(-3,-4) D、(-4,-3)8. 如图,在平面直角坐标系xOy中,已知直线AB与y轴交于点A(0,6),与x轴的负半轴交于点B , 且∠BAO=30°, M、N是该直线上的两个动点,且MN=2,连接OM、ON , 则△MON周长的最小值为 ( )
A、(-4,-5) B、(-5,-4) C、(-3,-4) D、(-4,-3)8. 如图,在平面直角坐标系xOy中,已知直线AB与y轴交于点A(0,6),与x轴的负半轴交于点B , 且∠BAO=30°, M、N是该直线上的两个动点,且MN=2,连接OM、ON , 则△MON周长的最小值为 ( ) A、2+3 B、2+2 C、2+2 D、5+9. 如图,△ABC中,∠B=90°,∠A=30°,E,F分别是边AB,AC上的点,连结EF,将△AEF沿着者EF折叠,得到△A'EF,当△A'EF的三边与△ABC的三边有一组边平行时,∠AEF的度数不可能是( )
A、2+3 B、2+2 C、2+2 D、5+9. 如图,△ABC中,∠B=90°,∠A=30°,E,F分别是边AB,AC上的点,连结EF,将△AEF沿着者EF折叠,得到△A'EF,当△A'EF的三边与△ABC的三边有一组边平行时,∠AEF的度数不可能是( ) A、120° B、105° C、75° D、45°10. 如图,E是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,CE的延长线交AD于F,连接BF,下列结论:①DE=DF;②△BEF为等腰三角形;③AF= CE;④BD的长等于四边形ABCD周长的 倍,其中正确的有( )个
A、120° B、105° C、75° D、45°10. 如图,E是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,CE的延长线交AD于F,连接BF,下列结论:①DE=DF;②△BEF为等腰三角形;③AF= CE;④BD的长等于四边形ABCD周长的 倍,其中正确的有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每题5分,共30分)
-
11. 如图所示,△ABO与△CDO称为“对顶三角形”,其中∠A+∠B=∠C+∠D.利用这个结论,在图2中,∠A+∠B+∠C+∠D+∠E+∠F+∠G=
 12. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.
12. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是. 13. 如图,在平行四边形ABCD中,点E是边AD上一点,CD=CE,连结BE,将△DCE 沿CE翻折,点D的对应点F恰好落在BE上,连结CF,若∠A=105°,△ABE的面积为 ,则ED= cm.
13. 如图,在平行四边形ABCD中,点E是边AD上一点,CD=CE,连结BE,将△DCE 沿CE翻折,点D的对应点F恰好落在BE上,连结CF,若∠A=105°,△ABE的面积为 ,则ED= cm.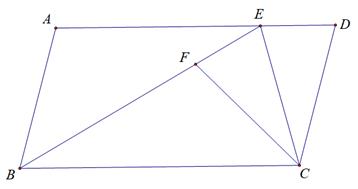 14. 如图1,在▱ABCD中(AB>BC),∠DAB=60°,对角线AC,BD相交于点E,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AEP的面积为y,y与x的函数关系图象如图2所示,当△AEP为等腰三角形时,x的值为 .
14. 如图1,在▱ABCD中(AB>BC),∠DAB=60°,对角线AC,BD相交于点E,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AEP的面积为y,y与x的函数关系图象如图2所示,当△AEP为等腰三角形时,x的值为 . 15. 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有次.
15. 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有次.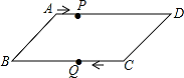 16. 如图所示,分别以 的直角边 ,斜边 为边向 外构造等边 和等边 , 为 的中点,连接 , , , , .有下列五个结论:① ;② ;③四边形 是菱形;④ ;⑤四边形 是平行四边形.其中正确的结论是 .
16. 如图所示,分别以 的直角边 ,斜边 为边向 外构造等边 和等边 , 为 的中点,连接 , , , , .有下列五个结论:① ;② ;③四边形 是菱形;④ ;⑤四边形 是平行四边形.其中正确的结论是 .
三、解答题(共8题,共80分)
-
17. 如图,在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°
求证:∠ADE=∠ADC。
 18. 如图所示,在ABCD中,分别以AB,CD为边向外作等边△ABE和等边△CDF,连结BD,EF。求证:EF与BD互相平分。
18. 如图所示,在ABCD中,分别以AB,CD为边向外作等边△ABE和等边△CDF,连结BD,EF。求证:EF与BD互相平分。 19. 如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
19. 如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点. (1)、求证:AF=CE;(2)、若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.20. 如图所示,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF//BC.
(1)、求证:AF=CE;(2)、若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.20. 如图所示,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF//BC. (1)、求证:四边形BDEF是平行四边形.(2)、线段BF,AB,AC的数量之间具有怎样的关系?证明你所得到的结论.21. 已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.
(1)、求证:四边形BDEF是平行四边形.(2)、线段BF,AB,AC的数量之间具有怎样的关系?证明你所得到的结论.21. 已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM. (1)、求证:△BAD≌△CAE;(2)、若∠ABC=30°,求∠MEC的度数;(3)、求证:四边形MBDE是平行四边形.22. 如图,在平面直角坐标系中, , ,直线 与x轴相交于点C,与直线AB交于点D,交y轴于点E.
(1)、求证:△BAD≌△CAE;(2)、若∠ABC=30°,求∠MEC的度数;(3)、求证:四边形MBDE是平行四边形.22. 如图,在平面直角坐标系中, , ,直线 与x轴相交于点C,与直线AB交于点D,交y轴于点E. (1)、求直线AB的解析式及点D的坐标;(2)、如图2,H是直线AB上位于第一象限内的一点,连接HC,当 时,点M、N为y轴上两动点,点M在点N的上方,且 ,连接HM、NC,求 的最小值;(3)、将△OEC 绕平面内某点转90°,旋转后的三角形记为 ,若点 落在直线AB上,点 落在直线CD上,请直接写出满足条件的点 的坐标.23. 如图,已知在矩形 中, ,点E在边 上,连接 ,以 为对称轴将 翻折得到 ,以 为邻边作 ,连接 ,延长 交直线 于H.
(1)、求直线AB的解析式及点D的坐标;(2)、如图2,H是直线AB上位于第一象限内的一点,连接HC,当 时,点M、N为y轴上两动点,点M在点N的上方,且 ,连接HM、NC,求 的最小值;(3)、将△OEC 绕平面内某点转90°,旋转后的三角形记为 ,若点 落在直线AB上,点 落在直线CD上,请直接写出满足条件的点 的坐标.23. 如图,已知在矩形 中, ,点E在边 上,连接 ,以 为对称轴将 翻折得到 ,以 为邻边作 ,连接 ,延长 交直线 于H. (1)、求证:四边形 为平行四边形.(2)、当 时,求 的面积.(3)、若 为等腰三角形,求此时 的长.24. 如图,平面直角坐标系中,已知点C的坐标为( ,﹣2),直线AB与x轴、y轴分别交于点A、点B,且点B的坐标为(0,3),∠BAO=30°.
(1)、求证:四边形 为平行四边形.(2)、当 时,求 的面积.(3)、若 为等腰三角形,求此时 的长.24. 如图,平面直角坐标系中,已知点C的坐标为( ,﹣2),直线AB与x轴、y轴分别交于点A、点B,且点B的坐标为(0,3),∠BAO=30°. (1)、求直线AB的解析式;(2)、若点D是y轴上一动点,点E( ,m)在直线AB上,当CD+DE取得最小值时,求出D、E两点的坐标;(3)、在(2)的条件下,是否存在点P使得以P、C、D、E为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
(1)、求直线AB的解析式;(2)、若点D是y轴上一动点,点E( ,m)在直线AB上,当CD+DE取得最小值时,求出D、E两点的坐标;(3)、在(2)的条件下,是否存在点P使得以P、C、D、E为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.