2022年浙教版数学八下期末复习阶梯训练:反比例函数(优生加练)
试卷更新日期:2022-04-04 类型:复习试卷
一、单选题
-
1. 如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y= (k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是( )
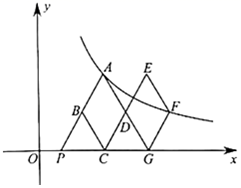 A、3 B、3 C、6 D、62. 如图,反比例函数y= (k>0)的图象经过矩形0ABC对角线的交点D,分别交AB、BC于点E、F。若四边形OEBF的面积为6,则k的值为( )
A、3 B、3 C、6 D、62. 如图,反比例函数y= (k>0)的图象经过矩形0ABC对角线的交点D,分别交AB、BC于点E、F。若四边形OEBF的面积为6,则k的值为( )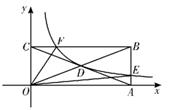 A、1 B、2 C、3 D、43. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图象经过点B , 若 ,则 的值为( ).
A、1 B、2 C、3 D、43. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图象经过点B , 若 ,则 的值为( ). A、6 B、3 C、 D、4. 如图,直线l⊥x轴于点P , 且与反比例函数 = (x>0)及 = (x>0)的图象分别交于点A、B , 连接OA、OB , 若△OAB的面积为3,则k1﹣k2的值为( )
A、6 B、3 C、 D、4. 如图,直线l⊥x轴于点P , 且与反比例函数 = (x>0)及 = (x>0)的图象分别交于点A、B , 连接OA、OB , 若△OAB的面积为3,则k1﹣k2的值为( )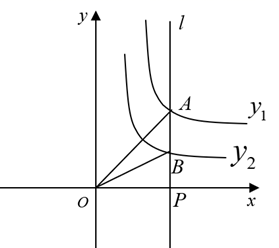 A、 B、3 C、6 D、95. 我们知道,方程x²+2x-1=0的解可看作函数y=x+2的图象与函数y= 的图象交点的横坐标。那么方程kx²+x-4=0(k≠0)的两个解其实就是直线y=kx+1与双曲线y= 的图象交点的横坐标。若这两个交点所对应的坐标为(x1 , )、(x2 , ),且均在直线y=x的同侧,则实数k的取值范围是( )A、 <k< B、 <k< C、 <k<0或0<k< D、 <k< 或 <k<06. 直线 与双曲线 交于A,B两点,若A,B两点的坐标分别为 , ,则 的值为( ).A、-4 B、0 C、4 D、87. 如图,点A,B在反比例函数y= (x<0)的图象上,连结OA,AB,以OA,AB为边作□OABC,若点C恰好落在反比例函数y= (x>0)的图象上,此时□OABC的面积是( )
A、 B、3 C、6 D、95. 我们知道,方程x²+2x-1=0的解可看作函数y=x+2的图象与函数y= 的图象交点的横坐标。那么方程kx²+x-4=0(k≠0)的两个解其实就是直线y=kx+1与双曲线y= 的图象交点的横坐标。若这两个交点所对应的坐标为(x1 , )、(x2 , ),且均在直线y=x的同侧,则实数k的取值范围是( )A、 <k< B、 <k< C、 <k<0或0<k< D、 <k< 或 <k<06. 直线 与双曲线 交于A,B两点,若A,B两点的坐标分别为 , ,则 的值为( ).A、-4 B、0 C、4 D、87. 如图,点A,B在反比例函数y= (x<0)的图象上,连结OA,AB,以OA,AB为边作□OABC,若点C恰好落在反比例函数y= (x>0)的图象上,此时□OABC的面积是( )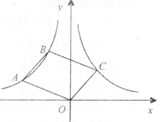 A、3 B、 C、 D、68. 如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
A、3 B、 C、 D、68. 如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )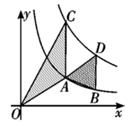 A、4 B、3 C、2 D、9. 在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )A、 B、 C、 D、10. 已知A(x1 , y1)、B(x2 , y2)、C(x3 , y3)是反比例函数y= 上的三点,若x1<x2<x3 , y2<y1<y3 , 则下列关系式不正确的是( )
A、4 B、3 C、2 D、9. 在平面直角坐标系中,反比例函数 的图象上有三点 ,若 且 ,则B的取值范围为( )A、 B、 C、 D、10. 已知A(x1 , y1)、B(x2 , y2)、C(x3 , y3)是反比例函数y= 上的三点,若x1<x2<x3 , y2<y1<y3 , 则下列关系式不正确的是( )
A、x1•x2<0 B、x1•x3<0 C、x2•x3<0 D、x1+x2<0二、填空题
-
11. 如图,矩形 的顶点A在y轴的正半轴上,顶点C在x轴的正半轴上,反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 , ,恰有 , ,若 ,则k的值是.
 12. 如图,已知菱形ABCD的对角线AC的中点与坐标原点重合,AF⊥AC交x轴于点F , 反比例函数 的图象经过点A , 与AF交于点E , 且AE=EF , △ADF的面积为6,则k的值为 .
12. 如图,已知菱形ABCD的对角线AC的中点与坐标原点重合,AF⊥AC交x轴于点F , 反比例函数 的图象经过点A , 与AF交于点E , 且AE=EF , △ADF的面积为6,则k的值为 .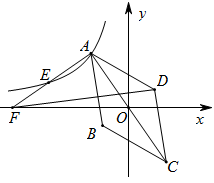 13. 如图,在平面直角坐标系 中,点 坐标为 ,以 为对角线作正方形 ,若顶点 在反比例函数 的图象上, 的值是.
13. 如图,在平面直角坐标系 中,点 坐标为 ,以 为对角线作正方形 ,若顶点 在反比例函数 的图象上, 的值是. 14. 如图,12个边长为1的正方形摆放在平面直角坐标系中,过点A(-1,0)的直线AB将这12个正方形面积相等的两部分,且直线与反比例函数y= (k<0)的图象交于点C , 与y轴交于点B , 若△AOB与△BOC的面积之比为1:3,则k的值为 .
14. 如图,12个边长为1的正方形摆放在平面直角坐标系中,过点A(-1,0)的直线AB将这12个正方形面积相等的两部分,且直线与反比例函数y= (k<0)的图象交于点C , 与y轴交于点B , 若△AOB与△BOC的面积之比为1:3,则k的值为 . 15. 如图,直线 与双曲线 相交于A、B两点,以AB为边作正方形ABCD,则正方形ABCD面积的最小值为 .
15. 如图,直线 与双曲线 相交于A、B两点,以AB为边作正方形ABCD,则正方形ABCD面积的最小值为 .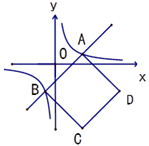 16. 如图,直线y=mx+n与双曲线y= (k>0,x>0)相交于点A(2,4),与y轴相交于点B(0,2),点C在该反比例函数的图象上运动,当△ABC的面积超过5时,点C的横坐标t的取值范围是.
16. 如图,直线y=mx+n与双曲线y= (k>0,x>0)相交于点A(2,4),与y轴相交于点B(0,2),点C在该反比例函数的图象上运动,当△ABC的面积超过5时,点C的横坐标t的取值范围是.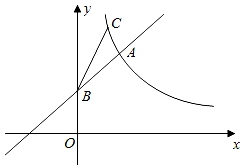
三、解答题
-
17. 已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y= (a≠0)的最大值与最小值之差是1,求a的值18. 已知y是x的反比例函数,且x=8时,y=12.写出y与x之间的函数关系式;19. 反比例函数y=(m-2)x2m+1的函数值为3时,求自变量x的值.
四、综合题
-
20. 反比例函数 (k≠0)和一次函数y=ax+2(a≠0)的图象交于第一象限内两点A(x1 , y1),B(x2 , y2),且0<x1<x2.记s=x1•y2 , t=x2•y1.(1)、若k=2,
①计算s•t的值.
②当1≤s<2时,求t的取值范围.
(2)、当s∶t=1∶4时,求y1和y2的值.21. 如图,直线 与 轴、 轴分别相交于点 、点 ,以线段 为边在第一象限作正方形 .反比例函数 在第一象限内的图象经过点 .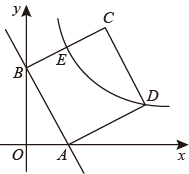 (1)、求反比例函数的解析式;(2)、将正方形 沿 轴向上平移几个单位能使点 落在(1)中所得的双曲线上?22. (性质认识)
(1)、求反比例函数的解析式;(2)、将正方形 沿 轴向上平移几个单位能使点 落在(1)中所得的双曲线上?22. (性质认识)如图,在函数 的图象上任取两点 、 向坐标轴作垂直,连接垂足 、 或 、 ,则一定有如下结论: , .
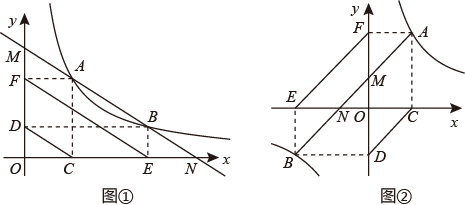 (1)、(数学理解)如图①,借助(性质认知)的结论,猜想 (填“>”、“=”或“<”);(2)、如图②,借助(性质认知)的结论,证明: ;(3)、(问题解决)如图③,函数 的图象与过原点的直线相交于 、 两点,点 是第一象限内图象上的动点(点 在点 的左侧),直线 分别交于 轴、 轴于点 、 ,连接 分别交 轴、 轴于点 、 .请证明: .
(1)、(数学理解)如图①,借助(性质认知)的结论,猜想 (填“>”、“=”或“<”);(2)、如图②,借助(性质认知)的结论,证明: ;(3)、(问题解决)如图③,函数 的图象与过原点的直线相交于 、 两点,点 是第一象限内图象上的动点(点 在点 的左侧),直线 分别交于 轴、 轴于点 、 ,连接 分别交 轴、 轴于点 、 .请证明: .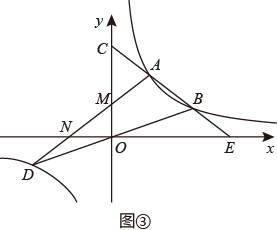 (4)、在第(3)问中,若 ,则 .23. 如图,在直角坐标系中,直线 与反比例函数 的图像交于关于原点对称的 , 两点,已知 点的纵坐标是3.
(4)、在第(3)问中,若 ,则 .23. 如图,在直角坐标系中,直线 与反比例函数 的图像交于关于原点对称的 , 两点,已知 点的纵坐标是3.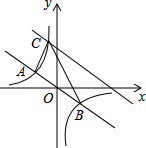 (1)、求反比例函数的表达式;(2)、根据图像直接写出 的解集;(3)、将直线 向上平移后与反比例函数在第二象限内交于点 ,如果 的面积为36,求平移后的直线的函数表达式.24. 当k值相同时,我们把正比例函数 和反比例函数 ,以函数y=﹣ x和y=﹣ ,下面是小亮的探究过程,请你将它补充完整.
(1)、求反比例函数的表达式;(2)、根据图像直接写出 的解集;(3)、将直线 向上平移后与反比例函数在第二象限内交于点 ,如果 的面积为36,求平移后的直线的函数表达式.24. 当k值相同时,我们把正比例函数 和反比例函数 ,以函数y=﹣ x和y=﹣ ,下面是小亮的探究过程,请你将它补充完整.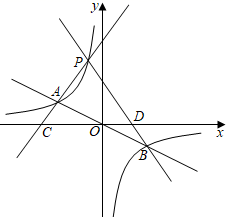 (1)、如图,在同一直角坐标系中画出这两个函数的图象,两个函数图象在第二、四象限分别交于点A,B,B的坐标分别是A , B.(2)、点P是函数y=﹣ 在第二象限内的图象上的一个动点(不与点A重合),作直线PA,分别与x轴交于点C,D.设点P的横坐标为t.小亮通过分析得到:在点P运动的过程中,总有PC=PD,
(1)、如图,在同一直角坐标系中画出这两个函数的图象,两个函数图象在第二、四象限分别交于点A,B,B的坐标分别是A , B.(2)、点P是函数y=﹣ 在第二象限内的图象上的一个动点(不与点A重合),作直线PA,分别与x轴交于点C,D.设点P的横坐标为t.小亮通过分析得到:在点P运动的过程中,总有PC=PD,证明PC=PD的过程如下(不完整).
易知点P的坐标是(t,﹣ ).
设直线AP的解析式为y=ax+b.
将点A,P的坐标分别代入,得 ,解得
∴直线AP的解析式为y=﹣ x﹣ .
令y=0,得x=t﹣2,则点C的坐标为(t﹣2,0).
同理可求得直线PB的解析式为y= x﹣ .
…
请你补充剩余的证明过程.
(3)、当△PCD是等边三角形时,t=.(4)、随着点P的运动,△ABP的面积S与点P的横坐标t之间存在一定的函数关系,当t>﹣2时,求S关于t的函数关系式.25. 已知反比例函数 图象经过一、三象限.(1)、判断点 在第几象限(2)、若点 , 是反比例函数 图象上的两点,试比较a,b,c的大小关系(3)、设反比例函数 ,已知 ,且满足当 时,函数 的最大值是 ;当 时,函数 的最小值是 .求x为何值时, .