浙教版数学八下专题复习：特殊平行四边形（优生集训）

试卷更新日期：2022-04-03 类型：复习试卷

进入出卷网下载

一、综合题

1. 在 $Δ A B C$ 中， $∠ B A C = 90^{°} ， A B = A C$ ，点 $D$ 为直线 $B C$ 上一动点（点 $D$ 不与 $B ， C$ 重合），以 $A D$ 为边在 $A D$ 右侧作正方形 $A D E F$ ，连接 $C F$

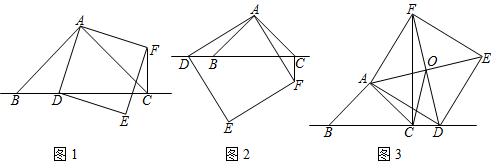(1)、探究猜想如图1，当点 $D$ 在线段 $B C$ 上时，
① $B C$ 与 $C F$ 的位置关系为；

② $B C ， C D ， C F$ 之间的数量关系为；

(2)、深入思考：如图2，当点 $D$ 在线段 $C B$ 的延长线上时，结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明.

(3)、拓展延伸如图3，当点 $D$ 在线段 $B C$ 的延长线上时，正方形 $A D E F$ 对角线交于点 $O$ .若已知 $A B = 2 \sqrt{2} ， C D = \frac{1}{4} B C$ ，请求出 $O C$ 的长.

查看试题解析
2. 如图所示，直线 $l ： y = - \frac{1}{2} x + 2 \sqrt{3}$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ 、 $B$ 两点，在 $y$ 轴上有一点 $C (0 ， 4 \sqrt{3})$ .

(1)、求 $△ A O B$ 的面积；

(2)、动点 $M$ 从 $A$ 点以每秒1个单位的速度沿 $x$ 轴向左移动，求 $△ C O M$ 的面积 $S$ 与 $M$ 的移动时间 $t$ 之间的函数关系式；

(3)、当动点 $M$ 在 $x$ 轴上移动的过程中，在平面直角坐标系中是否存在点 $N$ ，使以点 $A$ ， $C$ ， $N$ ， $M$ 为顶点的四边形为菱形，若存在，请直接写出点 $N$ 的坐标；若不存在，请说明理由.

查看试题解析
3. 如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是 $(- 6 ， 8)$ ．矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F ．

(1)、求点D的坐标；

(2)、若点N是平面内任一点，在x轴上是否存在点M ，使M、N、E、O为顶点的四边形是菱形？若存在，请直接写出满足条件的点M的坐标；若不存在，请说明理由．

查看试题解析
4. 如图

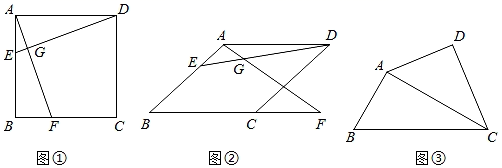
如图①，在正方形ABCD中，点E在AB上，点F在BC上，AF与DE相交于点G，AF＝DE，求证：∠DGF＝90°.

(1)、请完成上题的证明过程.

(2)、如图②，在菱形ABCD中，点E在AB上，点F在射线BC上，AF与DE相交于点G，AF＝DE，求证：∠DGF＝∠B.

(3)、如图③，已知四边形ABCD，利用直尺和圆规作线段EF，使点E、F分别在AB、CD上，且满足EF＝AC，EF与AC相交所形成的锐角等于∠B.

查看试题解析
5. 猜想与证明：如图①摆放矩形纸片ABCD与矩形纸片ECGF，使B，C，G三点在一条直线上，CE在边CD上．连结AF，若M为AF的中点，连结DM，ME，

(1)、试猜想DM与ME的数量关系，并证明你的结论．

(2)、拓展与延伸：
①若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为；

②如图②摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，猜想并证明DM和ME的关系．下面给出部分证明过程，请把推理过程补充完整．

证明：如图③，连结AC．

∵四边形ABCD、四边形ECGF都是正方形，

∴∠DAC=∠DCA＝∠DCE＝∠CFE＝45°，

∴点E在AC上．

∴∠AEF＝∠FEC＝90°．

又∵点M是AF的中点，

∴ME＝ $\frac{1}{2}$ AF．

查看试题解析
6. 如图，在平面直角坐标系 $x O y$ 中，直线 $O C ： y_{O C} = 3 x$ 与直线 $A C ： y_{A C} = - x + 8$ 相交于点 $C (2 ， 6)$ ．

(1)、点 $M$ 从点 $O$ 出发以每秒1个单位长度的速度沿 $x$ 轴向右运动，点 $N$ 从点 $A$ 出发以每秒3个单位长度的速度沿 $x$ 轴向左运动，两点同时出发.分别过点 $M$ ， $N$ 作 $x$ 轴的垂线，分别交直线 $O C$ ， $A C$ 于点 $P$ ， $Q$ ，请你在图1中画出图形，猜想四边形 $P M N Q$ 的形状（点 $M$ ， $N$ 重合时除外），并证明你的猜想；

(2)、在（1）的条件下，当点 $M$ 运动秒时，四边形 $P M N Q$ 是正方形（直接写出结论）．

查看试题解析
7. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x + 6$ 与x轴交于点A，与y轴交于点B，把△COB沿BC翻折，点O恰好落在AB边的点D处，BC为折痕．

(1)、求线段AB的长；

(2)、求直线BC的解析式；

(3)、若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
8. 将一块直角三角板的直角顶点和矩形ABCD（AB＜BC）的对角线的交点O重合，如图（①→②→③），图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点．

(1)、图①（三角板一直角边与OD重合）中，连接DN，则BN与DN的数量关系是，进而得到BN，CD，CN的数量关系是；

(2)、写出图③（三角板一边与OC重合）中，CN，BN，CD的数量关系是；

(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系，写出你的结论，并说明理由．

查看试题解析
9. 两个完全相同的矩形纸片ABCD ， BFDE按如图所示放置，已知AB＝BF＝8，BC＝16．

(1)、求证：四边形BHDG是菱形；

(2)、求四边形BHDG的周长．

查看试题解析
10. 反比例函数y₁= $\frac{k}{x}$ （x>0，k≠0）的图象经过点（1，3），点P是一次函数y₂=-x+6图象上的一个动点，如图所示，设点P的横坐标为m，且满足-m+6> $\frac{3}{m}$ ，过点P分别作PB⊥x轴，PA⊥y轴，垂足分别为B，A，与反比例函数分别交于D，C两点，连结OC，OD，CD．

(1)、求k的值并结合图象求出m的取值范围；

(2)、在点P运动过程中，若BD=2PD，求点P的坐标；．

(3)、将△OCD沿着直线CD翻折，点0的对应点为点O'，得到四边形O'COD，问：四边形O'COD能否为菱形？若能，求出点P坐标；若不能，说明理由。

查看试题解析
11. 已知矩形ABCD中，点E为AD上一点，连接BE、CE，∠BCE的平分线与AD交于点H，HG垂直平分BE，连接BH

(1)、如图1，①求证：△ABH≌△DCE；②若AE=8，BE=10，求△EHC的面积；

(2)、如图2，若∠ECD=30°，F是CE的中点，连接GF，判断四边形GFEH的形状，并证明。

查看试题解析
12. 如图，直线 $y = x + 3$ 与坐标轴交于点 $A$ 、 $B$ 两点，直线 $C P$ 与直线 $A B$ 相交于点 $P (\frac{1}{3} ， m)$ ，交 $x$ 轴于点 $C$ ，且 $Δ P A C$ 的面积为 $\frac{25}{3}$ .

(1)、求 $m$ 的值和点 $A$ 的坐标；

(2)、求直线 $P C$ 的解析式；

(3)、若点 $E$ 是线段 $A B$ 上一动点，过点 $E$ 作 $E Q / / x$ 轴交直线 $P C$ 于点 $Q$ ， $E M ⊥ x$ 轴， $Q N ⊥ x$ 轴，垂足分别为点 $M$ 、 $N$ ，是否存在点 $E$ ，使得四边形 $E M N Q$ 为正方形，若存在，请求出点 $E$ 坐标，若不存在，请说明理由.

查看试题解析
13. 已知：如图四边形ABCD是正方形，∠EAF＝45°.

(1)、如图1，若点E，F分别在边BC、CD上，延长线段CB至G，使得BG＝DF，若BE＝4，BG＝3，求EF的长；

(2)、如图2，若点E，F分别在边CB、DC延长线上时，求证：EF＝DF﹣BE；

(3)、如图3，如果四边形ABCD不是正方形，但满足AB＝AD，∠BAD＝∠BCD＝90°，∠EAF＝45°，且BC＝8，DC＝12，CF＝6，请你直接写出BE的长.

查看试题解析
14. 如图1，已知四边形 $A B C D$ 和四边形 $C E F G$ 都是正方形，且 $A B > C E$ .连接 $D E$ ，连接 $B G$ 交 $C D$ 于点 $M$ .如果正方形 $C E F G$ 绕点 $C$ 旋转到某一位置恰好使得 $C G // B D$ ，且 $B G = B D$ .

(1)、如 $B D = 2 \sqrt{3} + 2$ ， $C G = 2$ ，请求出 $△ B C G$ 的面积.

(2)、求证： $B M = \sqrt{2} D M$ .

(3)、如图2，当 $B D = 5 \sqrt{2}$ ， $M$ 是边 $C D$ 上一点且 $C M = 1$ 时，如点 $N$ 为 $B C$ 边上的一个动点，以 $M N$ 为边向左侧作等边 $△ M N P$ ，连接 $D P$ ，请直接写出 $D P$ 的最小值.

查看试题解析
15. 如图1，在矩形ABCD中，AM平分∠BAD，交BC于点M，点N是AD上的一点，连接MN，MD，且MN＝MD，过点D作DF⊥MN于F，DF延长线交AM于E，过点E作EP⊥AD于P.

(1)、如图1，①若CD＝5，AD＝7，求线段CM的长；
②求证：△PED≌△CMD.

(2)、如图2，过点F作FH⊥CD于H，当AM＝AD时，求 $\frac{A E}{F H}$ 的值.

查看试题解析
16. 在平面直角坐标系中，点A坐标为（0，4），点B坐标为（﹣3，0），连接AB，过点A作AC⊥AB交x轴于点C，点E是线段AO上的一动点.

(1)、如图1，当AE＝3OE时，
①求直线BE的函数表达式；

②设直线BE与直线AC交于点D，连接OD，点P是直线AC上的一动点（不与A，C，D重合），当S_△BOD＝S_△PDB时，求点P的坐标；

(2)、如图2，设直线BE与直线AC的交点F，在平面内是否存在点M使以点A，E，F，M为顶点的四边形是菱形？若存在，请直接写出点M的坐标；若不存在，请简述理由.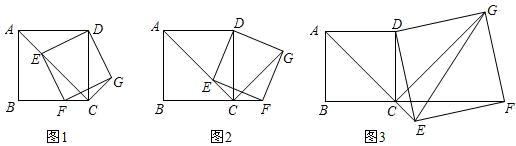

查看试题解析
17. 在正方形 $A B C D$ 中，点E为射线 $A C$ 上一点，连接 $D E$ ，过点E作 $E F ⊥ D E$ 交射线 $B C$ 于点F，以 $D E$ ， $E F$ 为邻边作矩形 $D E F G$ ，连接 $C G$ .

(1)、发现问题：如图1，当点E在线段 $A C$ 上时.
①求证四边形 $D E F G$ 是正方形；

②猜想 $C G$ 与 $A E$ 之间的数量关系，并说明理由.

(2)、类比探究：当点E运动到如图2所示的位置时，求 $∠ D C G$ 的度数.

(3)、拓展运用：如图3，当点E在线段 $A C$ 的延长线上时，若正方形 $A B C D$ 的边长为4， $C E = \sqrt{2}$ ，求 $G E$ 的长.

查看试题解析
18. 在平面直角坐标系中，直线y＝kx+8k（k是常数，k≠0）与坐标轴分别交于点A，点B，且点B的坐标为（0，6）.

(1)、求点A的坐标；

(2)、如图1，将直线AB绕点B逆时针旋转45°交x轴于点C，求直线BC的解析式；

(3)、在（2）的条件下，直线BC上有一点M，坐标平面内有一点P，若以A、B、M、P为顶点的四边形是菱形，请直接写出点P的坐标.

查看试题解析
19. 如图，直线 $y = - \frac{3}{4} x + 3$ 与直线 $y = \frac{1}{2} x + 3$ 相交于 $y$ 轴上一点 $C$ ，点 $P$ 是直线 $y = \frac{1}{2} x + 3$ 上的一个动点（不与点C重合），过点P作 $P M ⊥ x$ 轴交直线 $y = - \frac{3}{4} x + 3$ 于点M.设点P的横坐标为m.

(1)、直接写出点P，M的坐标P ， M（用含m的式子表示）；

(2)、若 $△ P C M$ 的面积为 $\frac{5}{2}$ ，求 $m$ 的值；

(3)、试探究在坐标平面内是否存在点N，使得以O，C，M，N为顶点的四边形是以CM为边的菱形？若存在，求出m的值，并直接写出点N的坐标；若不存在，说明理由.

查看试题解析
20. 如图，在正方形 ABCD 中，点 E 是对角线 BD 上一动点，AE 的延长线交 CD 于点 F，交 BC 的延长线于点 G，M 是 FG 的中点.

(1)、求证： ∠DAE=∠DCE；

(2)、判断线段 CE 与 CM 的位置关系，并证明你的结论；

(3)、当 $A D = \sqrt{3} + 1$ ，并且 $Δ C E G$ 恰好是等腰三角形时，求 DE 的长.

查看试题解析
21. 已知： $P$ 是正方形 $A B C D$ 对角线 $B D$ 上一点， $P E ⊥ D C ， P F ⊥ B C$ ，垂足分别为 $E ， F$ .

(1)、求证： $A P = P C$ ；

(2)、若 $∠ D A P = 30 ° ， P D = \sqrt{2}$ ，求 $E F$ 的长.

查看试题解析
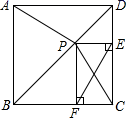22. 李明酷爱数学，勤于思考，善于反思．在学习八年级下册数学知识之后，他发现“二次根式、勾股定理、一次函数、平行四边形”都和“将军饮马”问题有关联，并且为解决“饮马位置”“最短路径长”等问题，提供了具体的数学方法．于是他撰写了一篇数学作文．请你认真阅读思考，帮助李明完成相关问题．
“将军饮马”问题的探究与拓展

八年级三班李明

“白日登山望烽火，黄昏饮马傍交河”（唐·李颀《古从军行》），这句诗让我想到了有趣的“将军饮马”问题：将军从 $A$ 地出发到河边 $l$ 饮马，然后再到 $B$ 地军营视察，怎样走路径最短？

（数学模型）如图1， $A$ ， $B$ 是直线 $l$ 同旁的两个定点．在直线 $l$ 上确定一点 $P$ ，使 $P A + P B$ 的值最小．

（问题解决）作点 $A$ 关于直线 $l$ 的对称点 $A^{'}$ ，连接 $A^{'} B$ 交 $l$ 于点 $P$ ，则点 $P$ 即为所求．此时， $P A + P B$ 的值最小，且 $P A + P B = A^{'} P + P B = A^{'} B$ ．

(1)、（模型应用）
问题1．如图2，经测量得 $A$ ， $B$ 两点到河边 $l$ 的距离分别为 $A C = 300$ 米， $B D = 900$ 米，且 $C D = 900$ 米．请计算出“将军饮马”问题中的最短路径长．

(2)、问题2．如图3，在正方形 $A B C D$ 中， $A B = 9$ ，点 $E$ 在 $C D$ 边上，且 $D E = 2 C E$ ，点 $P$ 是对角线 $A C$ 上的一个动点，则 $P E + P D$ 的最小值是．

(3)、问题3．如图4，在平面直角坐标系中，点 $A (- 2 ， 4)$ ，点 $B (4 ， 2)$ ．

请在 $x$ 轴上确定一点 $P$ ，使 $P A + P B$ 的值最小，并求出 $P$ 的坐标；

(4)、请直接写出 $P A + P B$ 的最小值．

(5)、（模型迁移）
问题4．如图5，菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $A C = 12$ ， $B D = 16$ ．点 $P$ 和点 $E$ 分别为 $B D$ ， $C D$ 上的动点，求 $P E + P C$ 的最小值．

查看试题解析
23. 如图，D是等边三角形ABC边BC上一点，DE∥AC交AB于点E ， B ， B′关于直线DE成轴对称，连接B′E ， B′D分别交AC于点F ， G ．

(1)、求证：四边形AEDG是平行四边形；

(2)、当四边形AEDG是菱形时，求这个菱形的面积与△ABC的面积之比；

(3)、当AB＝6，DE＝2AE时，直接写出四边形AEDG的两条对角线长AD＝， EG＝.

查看试题解析
24. 在菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，点 $P$ 是射线 $B D$ 上一动点，以 $A P$ 为边向右侧作等边 $△ A P E$ ，连接 $C E$ .

(1)、如图1，当点 $E$ 在边 $A D$ 上时，填空：
① $B P$ 与 $C E$ 的数量关系是，

② $C E$ 与 $A D$ 的位置关系是；

(2)、如图2，当点 $E$ 在菱形 $A B C D$ 外部时，（1）中的结论是否仍成立？若成立，请予以证明；若不成立，请说明理由.

(3)、如图3，在点 $P$ 的移动过程中，连接 $A C$ ， $D E$ ，若 $A B = 2$ ， $P D = 1$ ，请直接写出四边形 $A C D E$ 的面积值.

查看试题解析
25. 如图，在平面直角坐标系中， $O$ 为坐标原点，四边形 $O A B C$ 是矩形，点 $A$ ， $C$ 的坐标为 $A (10 ， 0)$ 、 $C (0 ， 4)$ ，点 $D$ 为 $O A$ 的中点.

(1)、求点 $B$ 的坐标；

(2)、求直线 $D B$ 的函数解析式；

(3)、点 $P$ 从点 $C$ 出发，以每秒1个单位的速度沿线段 $B C$ 向点 $B$ 运动，设运动时间为 $t$ ，当 $t$ 为何值时 $△ O D P$ 是腰长为5的等腰三角形？

查看试题解析