2022年浙教版数学八下期末复习阶梯训练：特殊平行四边形（基础巩固）
试卷更新日期：2022-04-03 类型：复习试卷
一、单选题
-
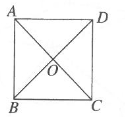
1. 如图所示，正方形ABCD的对角线AC，BD相交于点O，OA=3，则此正方形的面积为（ ）
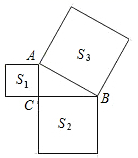
A、3 B、12 C、18 D、362. 下列四边形中，对角线互相垂直平分的是（ ）A、平行四边形、菱形 B、矩形、菱形 C、矩形、正方形 D、菱形、正方形3. 如图，字母B所代表的正方形的边长是（ ）
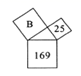A、194 B、144 C、13 D、124. 正方形具有而菱形不具有的性质是（ ）A、四条边都相等 B、对角线互相垂直 C、两组对角分别相等 D、四个角都是直角5. 菱形具有而矩形不一定有的性质是（ ）A、对角线互相平分 B、四条边都相等 C、对角相等 D、对边平行6. 正方形具有而矩形不具有的性质是（ ）A、对角相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直7. 下列说法正确的是（ ）A、对角线相等的四边形是矩形 B、对角线互相垂直且相等的四边形是正方形 C、对角线互相垂直平分的四边形是菱形 D、四边相等的四边形是正方形8. 下列命题中正确的是（ ）A、对角线互相垂直的平行四边形是正方形 B、一组对边平行，且有一个角是直角，一组邻边相等的四边形是正方形 C、对角线相等且互相垂直的四边形是正方形 D、对角线相等且互相垂直平分的四边形是正方形9. 菱形和矩形的对角线，具有的性质是下列的（ ）A、对角线相等 B、对角线互相垂直 C、对角线互相垂直平分 D、对角线互相平分10. 工人师傅在做门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形．这样做的道理是（ ）A、两组对边分别相等的四边形是矩形 B、有一个角是直角的平行四边形是矩形 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是矩形二、填空题
-
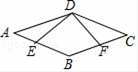
11. 在四边形ABCD中，对角线AC，BD交于点O，OA=OC=OB=OD，添加一个条件使四边形ABCD是正方形，那么所添加的条件可以是(写出一个即可)12. 如图， 分别以Rt△ABC三边构造三个正方形，面积分别为S1 ， S2 ， S3 ， 若S1=15，S3=39，则S2=.
13. 如图，矩形ABCD中，BE⊥AC于点E，若∠ACB＝35°，则∠DBE＝度.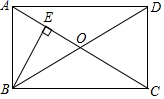
14. 矩形两条对角线的夹角为60°，对角线长为14，则该矩形较短边的边长为.15. 如图，已知菱形ABCD中，∠ABD＝70°，则∠ABC＝ ．
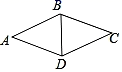16. 矩形ABCD的两条对角线相交于点O ， ∠AOB＝60°，AC＝4cm，则AB＝ ， 矩形ABCD的面积＝ ．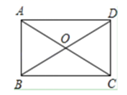
三、解答题
-
17. 如图，在菱形ABCD中，AC与BD相交于点E，若BD＝ ，菱形ABCD的周长为20，求菱形ABCD的面积.
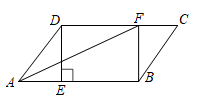
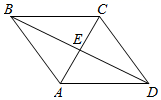18. 如图，在▱ABCD中，BE⊥CD，点E为垂足，AF=CE，求证：四边形BEDF是矩形．
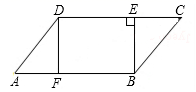19. 如图，在▱ABCD中，∠ABD＝90°，延长AB至点E，使BE＝AB，连接CE.求证：四边形BECD是矩形.
20. 如图，▱ABCD中对角线BD平分∠ABC.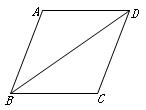
求证：▱ABCD是菱形.
21. 如图，已知菱形ABCD中，对角线AC、BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E.求证：四边形CODE是矩形；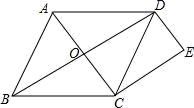
22. 如图，在菱形ABCD中，AC=8，BD=6． 请求出菱形ABCD的周长和面积．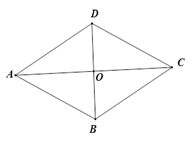
四、综合题
-
23. 如图，已知点M(－2，0)点N(0，6)，A为线段MN上一点，AB⊥ 轴，垂足为B，AC⊥ 轴，垂足为点C．
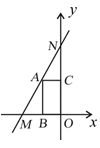(1)、求直线MN的函数表达式；(2)、若点A的横坐标为－1，求矩形ABOC的面积．
