2022年浙教版数学八下期中复习阶梯训练：平行四边形（优生集训）

试卷更新日期：2022-04-03 类型：复习试卷

进入出卷网下载

一、综合题

1. 化简、求解

(1)、若a，b，c是△ABC的三边的长，化简|a-b-c|+|b-c-a|+|c+a-b|.

(2)、已知一正多边形的内角与其相邻的外角的比为3：1，求该多边形的边数.

查看试题解析
2. 如图，在△OBC中，边BC的垂直平分线交∠BOC的平分线于点D，连接DB，DC，过点D作DF⊥OC于点F.

(1)、若∠BOC＝60°，求∠BDC的度数；

(2)、若∠BOC＝ $α$ ，则∠BDC＝；（直接写出结果）

(3)、直接写出OB，OC，OF之间的数量关系.

查看试题解析
3. 看对话答题：
小梅说：这个多边形的内角和等于1125°

小红说：不对，你少加了一个角

问题：

(1)、他们在求几边形的内角和?

(2)、少加的那个内角是多少度?

查看试题解析
4. 如图①，在Rt△ABC中，∠ACB＝90°，AC＝BC，l是过点C的任意一条直线，过A作AD⊥l于D，过B作BE⊥l于E.

(1)、求证：△ADC≌△CEB；

(2)、如图②延长BE至F，连接CF，以CF为直角边作等腰Rt△FCG，∠FCG＝90°，连接AG交l于H.求证：BF＝2CH.

(3)、在（2）的条件下，若AD＝12，BF＝15，BC＝13，请直接写出点G到直线AC的距离.

查看试题解析
5. 已知，在 $▱ A B C D$ 中， $A B ⊥ B D$ ， $A B ＝ B D$ ， $E$ 为射线 $B C$ 上一点，连接 $A E$ 交 $B D$ 于点 $F$ ．

(1)、如图1，若点 $E$ 与点 $C$ 重合，且 $A F = \sqrt{5}$ ，求 $A B$ 的长；

(2)、如图2，当点 $E$ 在 $B C$ 边上时，过点 $D$ 作 $D G ⊥ A E$ 于 $G$ ，延长 $D G$ 交 $B C$ 于 $H$ ，连接 $F H$ ．求证： $A F = D H + F H$ ；

(3)、如图3，当点 $E$ 在射线 $B C$ 上运动时，过点 $D$ 作 $D G ⊥ A E$ 于 $G$ ， $M$ 为 $A G$ 的中点，点 $N$ 在 $B C$ 边上且 $B N = 1$ ，已知 $A B = 5 \sqrt{2}$ ，请直接写出 $M N$ 的最小值．

查看试题解析
6. 如图，平面直角坐标系中，已知点C的坐标为（ $\sqrt{3}$ ，﹣2），直线AB与x轴、y轴分别交于点A、点B，且点B的坐标为（0，3），∠BAO＝30°.

(1)、求直线AB的解析式；

(2)、若点D是y轴上一动点，点E（ $\sqrt{3}$ ，m）在直线AB上，当CD+DE取得最小值时，求出D、E两点的坐标；

(3)、在（2）的条件下，是否存在点P使得以P、C、D、E为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由.

查看试题解析
7. 如图，直线l₁经过A（6，0）、B（0，8）两点，点C从B出发沿线段BO以每秒1个单位长度的速度向点O运动，点D从A出发沿线段AB以每秒2个单位长度的速度向点B运动，设运动时间为t秒（t＞0）.

(1)、求直线l₁的表达式；

(2)、当t＝时，BC＝BD；

(3)、将直线l₁沿x轴向右平移3个单位长度后，与x轴，y轴分别交于E、F两点，求四边形BAEF的面积；

(4)、在平面内，是否存在点P，使O、A、B、P四点为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由.

查看试题解析
8. 如图，在▱ABCD中，对角线AC ， BD相交于点O ， OA＝5cm ， E ， F为直线BD上的两个动点（点E ， F始终在▱ABCD的外面），连接AE ， CE ， CF ， AF ．

(1)、若DE＝ $\frac{1}{2}$ OD ， BF＝ $\frac{1}{2}$ OB ，
①求证：四边形AFCE为平行四边形；

②若CA平分∠BCD ， ∠AEC＝60°，求四边形AFCE的周长．

(2)、若DE＝ $\frac{1}{3}$ OD ， BF＝ $\frac{1}{3}$ OB ，四边形AFCE还是平行四边形吗？请写出结论并说明理由．若DE＝ $\frac{1}{n}$ OD ， BF＝ $\frac{1}{n}$ OB呢？请直接写出结论．

查看试题解析
9. 如图，直线 $y = - \frac{1}{2} x + 3$ 分别与 $x$ 轴、 $y$ 轴交于 $A ， B$ 两点，与直线 $y = x$ 交于点 $C$ ，过点 $C$ 平分△ $A O C$ 面积的直线交 $x$ 轴于点 $D$ .

(1)、求线段 $C D$ 的长；

(2)、点 $E$ 在 $y$ 轴上，当△ $D C E$ 周长最小时，求点 $E$ 的坐标（不用证明周长最小）；

(3)、点 $P$ 是直线 $A B$ 上的一个动点，在平面内是否存在点 $Q$ ，使以 $A 、 D 、 P 、 Q$ 为顶点的四边形是平行四边形，且面积等于△ $A O C$ 的面积？若存在，直接写出点 $Q$ 的坐标；若不存在，请说明理由.

查看试题解析
10. 如图，在平面直角坐标中，点A的坐标为（4，0），直线AB⊥x轴，直线y $= - \frac{1}{4}$ x+3经过点B，与y轴交于点C．

(1)、填空：点B的坐标为；

(2)、直线l经过点C，与直线AB交于点D，E是直线AB上一点，且∠ECD＝∠OCD，CE＝5，求直线l的解析式；

(3)、在（2）的条件下，点P在直线l上运动，点Q在直线OE上运动，若以P、Q、B、C为顶点的四边形为平行四边形，直接写出点P的坐标．

查看试题解析
11. 如图，在平面直角坐标系 $x O y$ 中，矩形 $A B C D$ 的 $A B$ 边在 $x$ 轴上， $A B = 3$ ， $A D = 2$ ，经过点 $C$ 的直线 $y = x - 2$ 与 $x$ 轴、 $y$ 轴分别交于点 $E$ 、 $F$ .

(1)、求点 $D$ 的坐标；

(2)、问直线 $y = x - 2$ 上是否在点 $P$ ，使得 $△ P D C$ 为等腰直角三角形？若存在，求出点 $P$ 的坐标；若不存在，请说明理由.

(3)、在平面直角坐标系内确定点 $M$ ，使得以点 $M$ 、 $D$ 、 $C$ 、 $E$ 为顶点的四边形是平行四边形，请直接写出点 $M$ 的坐标.

查看试题解析
12. 如图在平面直角坐标系之中，点 $O$ 为坐标原点，直线 $y = - \frac{3}{4} x + 3$ 分别交x、y轴于点 $B$ 、 $A$ .

(1)、如图1，点 $C$ 是直线 $A B$ 上不同于点 $B$ 的点，且 $C A = A B$ .则点 $C$ 的坐标为

(2)、点 $C$ 是直线 $A B$ 外一点，满足 $∠ B A C = 45 °$ ，求出直线 $A C$ 的解析式.

(3)、如图2，点 $D$ 是线段 $O B$ 上一点，将 $△ A O D$ 沿直线 $A D$ 翻折，点 $O$ 落在线段 $A B$ 上的点E处，点M在射线 $D E$ 上，在x轴的正半轴上是否存在点N，使以M、A、N、B为顶点的四边形是平行四边形？若存在，请求出点N的坐标；若不存在，请说明理由.

查看试题解析
13. 如图，在平面直角坐标系中，直线 $y = - \frac{\sqrt{3}}{2} x - 2 \sqrt{3}$ 与x轴，y轴分别交于点A，C，经过点C的直线与x轴交于点B（2，0）.

(1)、求直线BC的解析式；

(2)、点P是线段AC上一动点，若直线BP把△ABC的面积分成1：2的两部分，请求点P的坐标；

(3)、若点P是直线AC上一动点，点E是坐标轴上一动点，则是否存在动点P使以点B，C，P，E为顶点的四边形是以BC为一边的平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由.

查看试题解析
14. 如图所示，在直角坐标系中，直线l与x轴y轴交于A、B两点，已知点A的坐标是（4，0），B的坐标是（0，3）.

(1)、求直线l的解析式；

(2)、若点C（3，0）是线段OA上一定点，点P（x，y）是第一象限内直线l上一动点，试求出点P在运动过程中△POC的面积S与x之间的函数关系式，并写出x的取值范围；

(3)、在（2）问的条件下，若S＝ $\frac{9}{4}$ ，此时在坐标平面内是否存在点Q，使以A，C，P，Q为顶点，以AC为边的四边形是平行四边形？若存在，直接写出点Q的坐标；若不存在，说明理由.

查看试题解析
15. 如图，在 $▱ A B C D$ 中， $∠ A B C = 60 °$ ， $∠ B A D$ 的平分线交 $C D$ 于点 $E$ ，交 $B C$ 的延长线于点 $F$ ，连接 $D F$ .

(1)、求证： $△ A B F$ 是等边三角形；

(2)、过点 $F$ 作 $F G ⊥ E C$ 于 $G$ ，若 $A D = 1$ ， $A B = 3$ ，求 $D F$ 的长度.

查看试题解析
16. 如图，平面直角坐标系中，直线AB分别交x轴、y轴正半轴于A、B两点，且 $O A = 2$ ， $O B = 1$ ，点C在y轴负半轴上，且 $A B ： B C = 1 ： \sqrt{5}$ .

(1)、求直线AC的函数解析式；

(2)、若P是线段CA上的一动点，且从点C出发，由点C向点A以每秒2个单位长度的速度匀速运动，连接BP，设 $△ A B P$ 的面积为S，点P的运动时间为t秒，写出s关于t的函数关系式，并直接写出自变量t的取值范围；

(3)、若P是直线AC上的一动点，Q是直线AB上的一动点，是否存在一点P使以O，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由.

查看试题解析
17. 如图，在平面直角坐标系中，已知点A（1，0），将x轴绕点A顺时针旋转60°交y轴于点B，再将点B绕点A顺时针旋转90°得到点C.

(1)、求直线BC的解析式；

(2)、若点Q为平面直角坐标系中一点，且满足四边形ABCQ为平行四边形，求点Q的坐标；

(3)、在直线BC和y轴上，是否分别存在点M和点N，使得以点M，N，A，C为顶点的四边形为平行四边形？若存在，请直接写出点M的坐标；若不存在，说明理由.

查看试题解析
18. 已知AM是△ABC的中线，D是线段AM上一点（不与点A重合）.过点D作AB的平行线，过点C作AM的平行线，两线交于点E，连结AE.

(1)、（模型研究）如图1，当点D与M重合时，求证：四边形ABDE是平行四边形；

(2)、（模型推广）如图2，当点D不与M重合时，四边形ABDE还是平行四边形吗？如果是，请证明；如果不是，请说明理由；

(3)、（模型应用）若△ABC是边长为4的等边三角形，点D是AM的中点（如图3），请直接写出CE的长.

查看试题解析
19. 如图，平面直角坐标系中，直线 $y = k x + b$ 经过点 $A (2 ， 0)$ ， $D (0 ， 1)$ ，点 $B$ 是第一象限的点且 $A B = \sqrt{5}$ ，过点 $B$ 作 $B C ⊥ y$ 轴，垂足为 $C$ ， $C B = 1$ ．

(1)、直线 $y = k x + b$ 的解析式；

(2)、求点 $B$ 坐标；

(3)、若点 $M$ 是直线 $A D$ 上的一个动点，在 $x$ 轴上存在另一个点 $N$ ，且以 $O$ 、 $B$ 、 $M$ 、 $N$ 为顶点的四边形是平行四边形，请直接写出点 $N$ 的坐标．

查看试题解析
20. 如图，在 $▱ A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，点 $E$ ， $F$ 分别为 $O B$ ， $O D$ 的中点．

(1)、求证： $△ A B E ≌ △ C D F$ ；

(2)、延长 $A E$ 至 $G$ ，使 $E G = A E$ ，连接 $C G$ ，延长 $C F$ ，交 $A D$ 于点 $P$ ．
①当 $A B$ 与 $A C$ 满足什么数量关系时，四边形 $E G C F$ 是矩形？请说明理由；

②若 $A P = 2 D P = 8$ ， $C P = \sqrt{17}$ ， $C D = 5$ ，求四边形 $E G C F$ 的面积．

查看试题解析
21. 综合与实践：

【问题情境】

在数学综合实践课上，老师让同学用两张全等的等腰三角形纸片进行拼摆，并探究摆放后所构成的图形之间的关系．如图1， $△ A B C ≌ △ D E F$ ， $A B = A C$ ， $D E = D F$ ．

(1)、【猜想探究】
“勤奋小组”的同学把这两张纸片按如图2的方式摆放，点A与点D重合，连接 $B E$ 和 $C F$ ．他们发现 $B E$ 和 $C F$ 之间存在着一定的数量关系，这个关系是．

(2)、【类比验证】
“创新小组”的同学在“勤奋小组”的启发下，把这两张纸片按如图3的方式摆放，点F，A，D，C在同一直线上，连接 $B F$ 和 $C E$ ，他们发现了 $B F$ 和 $C E$ 之间的数量和位置关系，请写出这些关系并说明理由；

(3)、【操作展示】
请你利用 $△ A B C$ 和 $△ D E F$ 纸片进行拼摆，将拼摆出的图形画在图4中（要求不得与图2，图3相同），并根据图形写出一条正确的数学结论．

查看试题解析
22. 如图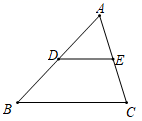

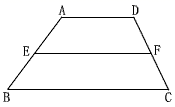
(1)、如图，已知△ABC中，D、E分别是AB、AC的中点，求证：DE∥BC，DE= $\frac{1}{2}$ BC.

(2)、利用第（1）题的结论，解决下列问题：
①如图，在四边形ABCD中，AD∥BC，E、F分别是AB、CD的中点，求证：EF∥BC，FE= $\frac{1}{2}$ （AD+BC）

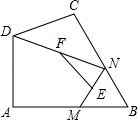
②如图，在四边形ABCD中，∠A＝90°，AB＝3 $\sqrt{3}$ ，AD＝3，点M，N分别在边AB，BC上，点E，F分别为MN，DN的中点，连接EF，求EF长度的最大值.

查看试题解析
23.

(1)、如图1，∠ADC=120°，∠BCD=140°，∠DAB和∠CBE的平分线交于点F，则∠AFB的度数是；

(2)、如图2，若∠ADC= $α$ ， ∠BCD= $β$ ，且 $α + β > 180 °$ ， ∠DAB和∠CBE的平分线交于点F，则∠AFB=（用含 $α$ ， $β$ 的代数式表示）；

(3)、如图3，∠ADC= $α$ ， ∠BCD= $β$ ，当∠DAB和∠CBE的平分线AG，BH平行时， $α$ ， $β$ 应该满足怎样的数量关系？请说明理由；

(4)、如果将（2）中的条件 $α + β > 180 °$ 改为 $α + β < 180 °$ ，再分别作∠DAB和∠CBE的平分线，∠AFB与 $α$ ， $β$ 满足怎样的数量关系？请画出图形并直接写出结论.

查看试题解析
24. 如图，在四边形 $A B C D$ 中， $∠ B A D$ 的角平分线与边 $B C$ 交于点E， $∠ A D C$ 的角平分线交直线 $A E$ 于点O.

(1)、若点O在四边形 $A B C D$ 的内部，
①如图，若 $A D / / B C$ ， $∠ B = 40^{°}$ ， $∠ C = 70^{°}$ ，则 $∠ D O E =$ （）；

②如图，试探索 $∠ B$ 、 $∠ C$ 、 $∠ D O E$ 之间的数量关系，并将你的探索过程写下来.

(2)、如图，若点O是四边形 $A B C D$ 的外部，请你直接写出 $∠ B$ 、 $∠ C$ 、 $∠ D O E$ 之间的数量关系.

查看试题解析
25. 如图，在四边形 $A B C D$ 中， $B E$ 和 $D F$ 分别平分四边形的外角 $∠ M B C$ 和 $∠ N D C$ ， $B E$ 与 $D F$ 相交于点 $G$ ，若 $∠ B A D = α ， ∠ B C D = β$ ．

(1)、如图1，若 $α + β = 168 °$ ，求 $∠ M B C + ∠ N D C$ 的度数；

(2)、如图1，若 $∠ B G D = 35 °$ ，试猜想 $α 、 β$ 所满足的数量关系式，并说明理由．

(3)、如图2，若 $α = β$ ，判断 $B E 、 D F$ 的位置关系，并说明理由．

查看试题解析