2022年浙教版数学八下期中复习阶梯训练：平行四边形（优生加练）

试卷更新日期：2022-04-03 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在平面直角坐标系xOy中，已知直线AB与y轴交于点A（0，6），与x轴的负半轴交于点B ，且∠BAO＝30°， M、N是该直线上的两个动点，且MN＝2，连接OM、ON ，则△MON周长的最小值为（）

A、2＋3 $\sqrt{2}$ B、2＋2 $\sqrt{10}$ C、2＋2 $\sqrt{13}$ D、5＋ $\sqrt{13}$

查看试题解析
2. 将一长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（）

A、360° B、540° C、720° D、730°

查看试题解析
3. 如图，△ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的个数（）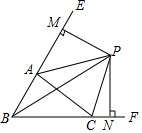

①CP平分∠ACF；②∠ABC+2∠APC=180°；③∠ACB=2∠APB；④S_△PAC=S_△MAP+S_△NCP.

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，由两个全等菱形(菱形ABCD与菱形EFGH)组成的“四叶草”图案，其重叠部分是正八边形(阴影部分)，点B，D在EG上，点F，H在AC上，若CF=2，则BD的长为（）

A、4 B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ D、2 $\sqrt{5}$

查看试题解析
5. 如图，在 $▱ A B C D$ 中， $A B = 4$ ， $B C = 8$ ， $∠ B = 60 °$ .分别以点B、D为圆心，大于 $\frac{1}{2} B D$ 长为半径画弧，两弧相交于点M、N，直线MN分别与AD、BC相交于点E、F，则EF的长为（）

A、 $\frac{4}{5} \sqrt{21}$ B、4 C、 $\frac{3}{5} \sqrt{21}$ D、 $\sqrt{13}$

查看试题解析
6. 如图，平行四边形ABCD中，对角线AC、BD相交于O，BD=2AD，E，F，G分别是OC，OD，AB的中点，下列结论：①四边形BEFG是平行四边形；②BE⊥AC；③EG=FG；④EA平分∠GEF。其中正确的是（）

A、①② B、①②③ C、①②④ D、①③④

查看试题解析
7. 平行四边形 $A B C D$ 中， $∠ A C B = 45 °$ ， $A C$ ， $B D$ 交于点 $O$ ， $E$ 是 $B C$ 边上一点，连接 $A E$ ，过点 $B$ 作 $B F ⊥ A E$ 并延长交 $A C$ 于点 $G$ ，交 $C D$ 于点 $H$ ，已知 $A B = A E$ ， $A F = 3$ ， $E F = 1$ ，则下列结论：① $∠ B A E = 2 ∠ C B H$ ；② $S_{△ A B E} = 2 \sqrt{7}$ ；③ $B E = \sqrt{2} C O$ ；④ $G H = C H$ 中正确的个数是（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ，点 $D$ 在边 $A C$ 上， $A B = 2$ ， $B D = C D$ ， $B C = 2 A B$ .若 $△ A B D$ 与 $△ E B D$ 关于直线 $B D$ 对称，则线段 $C E$ 的长为（）

A、 $\frac{6 \sqrt{5}}{5}$ B、 $\frac{7 \sqrt{5}}{5}$ C、 $\frac{8 \sqrt{5}}{5}$ D、 $\frac{9 \sqrt{5}}{5}$

查看试题解析
9. 如图，已知▱OABC的顶点A，C分别在直线 $x = 1$ 和 $x = 4$ 上，O是坐标原点，则对角线OB长的最小值为（）

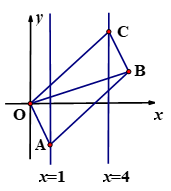A、3 B、4 C、5 D、6

查看试题解析
10. 如图，平行四边形ABCD中，AB=6，BC=4，∠DAB=60°，E在AB上，且AE= $\frac{1}{2}$ EB，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP：DQ的值为（）

A、 $\frac{\sqrt{39}}{13}$ B、 $\frac{2 \sqrt{13}}{13}$ C、 $\frac{2 \sqrt{39}}{39}$ D、 $\frac{2 \sqrt{39}}{13}$

查看试题解析

二、填空题

11. 如图所示，△ABO与△CDO称为“对顶三角形”，其中∠A+∠B=∠C+∠D．利用这个结论，在图2中，∠A+∠B+∠C+∠D+∠E+∠F+∠G= $°$

查看试题解析
12. 如图，矩形 $A B C D$ 中， $A B = 2 \sqrt{3}$ ， $B C = 4$ ，连结对角线 $A C$ ，E为 $A C$ 的中点，F为 $A B$ 边上的动点连结 $E F$ ，作点C关于 $E F$ 的对称点 $C^{'}$ ，连结 $C^{'} E$ ， $C^{'} F$ ，若 $△ E F C^{'}$ 与 $△ A C F$ 的重叠部分（ $△ E F G$ ）面积等于 $△ A C F$ 的 $\frac{1}{4}$ ，则 $B F =$ .

查看试题解析
13. 如图所示，分别以 $Rt △ A B C$ 的直角边 $A C$ ，斜边 $A B$ 为边向 $△ A B C$ 外构造等边 $△ A C D$ 和等边 $△ A B E$ ， $F$ 为 $A B$ 的中点，连接 $C F$ ， $D F$ ， $E F$ ， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ．有下列五个结论：① $A C ⊥ D F$ ；② $D A + D F = B E$ ；③四边形 $A D C F$ 是菱形；④ $S_{四边形 B C D E} = 6 S_{△ A C D}$ ；⑤四边形 $B C D F$ 是平行四边形．其中正确的结论是．

查看试题解析
14. 如图，在 $Δ A B C$ 中， $∠ B A C = 60 °$ ， $∠ A B C = 45 °$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点 $D$ . $P$ 为直线 $A B$ 上一动点.以 $D P$ 、 $B D$ 为邻边构造平行四边形 $D P Q B$ ，连接 $C Q$ ，若 $A C = 4$ .则 $C Q$ 的最小值为.

查看试题解析
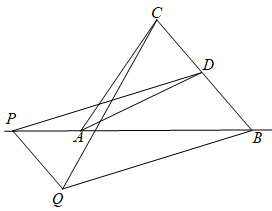15. 如图，▱ABCD中，AC，BD交于O，AE平分∠BAD，EC＝CD＝1，∠ECD＝2∠CDA.下列结论：①AC平分∠EAD；②OE＝ $\frac{1}{4}$ AD；③BD＝ $\sqrt{7}$ ；④S▱ABCD＝ $\sqrt{3}$ .正确的有个.

查看试题解析
16. 如图，平面直角坐标系 $x O y$ 中，点A在第一象限， $B (2 ， 0)$ ， $∠ A O B = 60 °$ ， $∠ A B O = 90 °$ ．在x轴上取一点 $P (m ， 0)$ ，过点P作直线l垂直于直线 $O A$ ，将线段 $O B$ 关于直线l的对称图形记为线段 $O^{'} B^{'}$ ，当线段 $O^{'} B^{'}$ 和过点A且平行于x轴的直线有交点时，m的取值范围为．

查看试题解析

三、解答题

17. 已知：如图，在四边形 $A B C D$ 中， $A D = B C$ ， $P$ 为对角线 $B D$ 的中点， $M$ 为 $A B$ 的中点， $N$ 为 $D C$ 的中点.求证： $∠ P M N = ∠ P N M$

查看试题解析
18. 【知识链接】连结三角形两边中点的线段，叫做三角形的中位线．
【动手操作】小明同学在探究证明中位线性质定理时，是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形，从而得出：三角形中位线平行于第三边且等于第三边的一半．

【性质证明】小明为证明定理，他想利用三角形全等、平行四边形的性质来证明．请你帮他完成解题过程（要求：画出图形，根据图形写出已知、求证和证明过程）．

查看试题解析
19. 在 $Δ A B C$ 中， $A B = A C$ ，点 $P$ 为 $Δ A B C$ 所在平面内一点，过点 $P$ 分别作 $P E ∥ A C$ 交 $A B$ 于点 $E$ ， $P F ∥ A B$ 交 $B C$ 于点 $D$ ，交 $A C$ 于点 $F$ .

若点 $P$ 在 $B C$ 上（如图①），此时 $P D = 0$ ，可得结论： $P D + P E + P F = A B$ .

请应用上述信息解决下列问题：

当点 $P$ 分别在 $Δ A B C$ 内（如图②）， $Δ A B C$ 外（如图③）时，上述结论是否成立？若成立，请给予证明；若不成立， $P D$ ， $P E$ ， $P F$ ，与 $A B$ 之间又有怎样的数量关系，请写出你的猜想，不需要证明.

查看试题解析
20. 如图，四边形 $A B C D ， C D / / A B ， A D = B C$ ，对角线 $A C 、 B D$ 交于点 $O$ ， $∠ A C D = 60 °$ ，点 $P 、 Q 、 S$ 分别为 $O A 、 B C 、 O D$ 的中点，求证： $Δ S P Q$ 是等边三角形.

查看试题解析
21. 如图，△ABC中，D为BC的中点。DE平分∠ADB，DF平分∠ADC，BE⊥DE，CF⊥DF，P为AD与EF的交点。证明：EF=2PD．

查看试题解析
22. 如图所示，在形状为平行四边形的一块地ABCD中，有一条小折路EFG．现在想把它改为经过点G的直路，要求小路两侧土地的面积都不变，请在图中画出改动后的小路．

查看试题解析
23. 如图，△ABC中，AB=8，AC=6，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，求线段EF的长．

查看试题解析
24. 已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC， $A B = 2 \sqrt{3}$ ．E是边AB的中点，联结DE、CE，且DE⊥CE．设AD=x，BC=y．

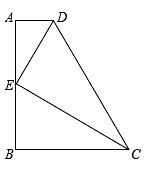(1)、如果∠BCD=60°，求CD的长；

(2)、求y关于x的函数解析式，并写出自变量x的取值范围；

(3)、联结BD．如果△BCD是以边CD为腰的等腰三角形，求x的值．

查看试题解析

四、综合题

25. 如图，在△ABC中，AC=BC，AD⊥AB交BE延长线于点D，CG平分∠ACB交BD于点F，交AB于点G，∠ADB=∠ACB.

(1)、若E为AC的中点，求证：AD=CF；

(2)、若BD=2，求BF值；

(3)、若CG=5，求AD+BD的值.

查看试题解析
26. 如图，AC平分∠BAD，∠DCA＝∠CAD，在CD的延长线上截取DE＝DA，连接AE.

(1)、求证：AB∥CD；

(2)、若AE＝5，AC＝12，求线段CE的长；

(3)、在（2）的条件下，若线段CE上有一点P，使△DPA的面积是△ACD面积的六分之一，求PC长.

查看试题解析