2022年浙教版数学八下期中复习阶梯训练：一元二次方程（优生加练）

试卷更新日期：2022-04-03 类型：复习试卷

进入出卷网下载

一、单选题

1. 一元二次方程 $M ： a x^{2} + b x + c = 0 ； N ： c x^{2} + b x + a = 0$ ，其中 $a c \neq 0 ， a \neq c$ ，给出以下四个结论：(1)若方程 $M$ 有两个不相等的实数根，则方程 $N$ 也有两个不相等的实数根；(2)若方程 $M$ 的两根符号相同，则方程 $N$ 的两根符号也相同；(3)若 $m$ 是方程 $M$ 的一个根，则 $\frac{1}{m}$ 是方程 $N$ 的一个根；(4)若方程 $M$ 和方程 $N$ 有一个相同的根，则这个根必是 $x = 1$ .其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 关于 $x$ 的一元二次方程 $x^{2} + 2 m x + 2 n = 0$ 有两个整数根且乘积为正，关于 $y$ 的一元二次方程 $y^{2} + 2 n y + 2 m = 0$ 同样也有两个整数根且乘积为正，给出三个结论：①这两个方程的根都负根；② ${(m - 1)}^{2} + {(n - 1)}^{2} \geq 2$ ；③ $- 1 \leq 2 m - 2 n \leq 1$ ，其中正确结论的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 有两个一元二次方程：M：ax²＋bx＋c＝0，N：cx²＋bx＋a＝0，以下四个结论中，错误的是（）

A、如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 B、如果方程M有两根符号相同，那么方程N也有两根符号相同 C、如果5是方程M的一个根，那么 $\frac{1}{5}$ 是方程N的一个根 D、如果方程M和方程N有一个相同的实数根，那么这个根必是x＝1

查看试题解析
4. 欧几里得是古希腊数学家，所著的《几何原本》闻名于世．在《几何原本》中，形如x²+ax＝b²的方程的图解法是：如图，以 $\frac{a}{2}$ 和b为直角边作Rt△ABC，再在斜边上截取BD＝ $\frac{a}{2}$ ，则图中哪条线段的长是方程x²+ax＝b²的解？答：是（）

A、AC B、AD C、AB D、BC

查看试题解析
5. 设a、b为x²+x﹣2011=0的两个实根，则a³+a²+3a+2014b=（）

A、2014 B、﹣2014 C、2011 D、﹣2011

查看试题解析
6. 若关于x的一元二次方程x²﹣3x+p=0（p≠0）的两个不相等的实数根分别为a和b，且a²﹣ab+b²=18，则 $\frac{a}{b}$ + $\frac{b}{a}$ 的值是（）

A、3 B、﹣3 C、5 D、﹣5

查看试题解析
7. 关于x的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有两个实数根，那么实数k的取值范围是（）

A、 $k \leq 1$ B、 $k < 1$ 且 $k \neq 0$ C、 $k \leq 1$ 且 $k \neq 0$ D、 $k \geq 1$

查看试题解析
8. 已知b²-4ac是一元二次方程ax²+bx+c=0(a≠0)的一个实数根，则ab的取值范围为（）

A、 $a b \geq \frac{1}{8}$ B、 $a b \geq \frac{1}{4}$ C、 $a b \leq \frac{1}{8}$ D、 $a b \leq \frac{1}{4}$

查看试题解析
9. 设a、b、c和S分别为三角形的三边长和面积，关于x的方程b²x²+(b²+c²-a²)x+c²=0的判别式为Δ.则Δ与S的大小关系为( ).

A、Δ=16S² B、Δ=-16S² C、Δ=16S D、Δ=-16S

查看试题解析
10. 已知实数 $x$ 满足 $x^{2} + \frac{1}{x^{2}} + x - \frac{1}{x} = 4$ ，则 $x - \frac{1}{x}$ 的值是（　　）．

A、-2 B、1 C、-1或2 D、-2或1

查看试题解析
11. 某农户种植花生，原来种植的花生亩产量为200千克，出油率为50％（即每100千克花生可加工成花生油50千克）．现在种植新品种花生后，每亩收获的花生可加工成花生油132千克，其中花生出油率的增长率是亩产量的增长率的 $\frac{1}{2}$ ．则新品种花生亩产量的增长率为（）

A、20％ B、30% C、50% D、120%

查看试题解析

二、填空题

12. 已知实数满足，则 $x^{2} + y^{2} + z^{2}$ 的值是.

查看试题解析
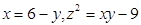13. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若（x﹣1）（mx﹣n）＝0是倍根方程，则 $\frac{2 n}{m}$ 的值为.

查看试题解析
14. 关于x的方程（1-m²）x²+2mx-1=0的所有根都是比1小的正实数，则实数m的取值范围是．

查看试题解析
15. 某商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个，第二周若按每个10元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售，销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出，如果这批旅游纪念品共获利1250元，则第二周每个旅游纪念品的销售价格为元.

查看试题解析
16. 设x₁ ， x₂是一元二次方程x²+5x﹣3=0的两根，且2x₁（x₂²+6x₂﹣3）+a=4，则a= ．

查看试题解析
17. 在△ABC中，已知两边a=3，b=4，第三边为c．若关于x的方程 $x^{2} + (c - 4) x + \frac{1}{4} = 0$ 有两个相等的实数根，则该三角形的面积是

查看试题解析
18. 对于实数a、b定义：a*b=a+b，a#b=ab，如：2*（﹣1）=2+（﹣1）=1，2#（﹣1）=2×（﹣1）=﹣2．以下结论：
①[2+（﹣5）]#（﹣2）=6；
②（a*b）#c=c（a*b）；
③a*（b#a）=（a*b）#a；
④若x＞0，且满足（1*x）#（1#x）=1，则x= $\frac{\sqrt{5} - 1}{2}$ ．
正确的是（填序号即可）

查看试题解析

三、解答题

19. 已知a、b、c是等腰△ABC的三边长，其中a＝4，b和c是关于x的方程x²-mx+3m＝0的两根，求m的值．

查看试题解析
20. 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况，下面是调查后小张与其他两位成员交流的情况．
小张：“该商品的进价为24元/件．”

成员甲：“当定价为40元/件时，每天可售出480件．”

成员乙：“若单价每涨1元，则每天少售出20件；若单价每降1元，则每天多售出40件．”根据他们的对话，请你求出要使该商品每天获利7680元，应该怎样合理定价？

查看试题解析
21. 在新冠肺炎流行中，某商家预测库存的带防护面罩的遮阳帕将能畅销市场预计平均每天可售出20件，每件赢利40元，为了扩大销售，增加赢利，回笼资金，商场决定采取适当的降价措施，经调查发现，如果每个遮阳帽每降价1元，商场平均每天可多售出2个，若商场平均每天要赢利1200元，每个遮阳帽应降价多少元？

查看试题解析
22. 阅读下面的例题：解方程x²﹣|x|﹣2＝0
解：当x≥0时，原方程化为x²﹣x﹣2＝0，解得：x₁＝2，x₂＝﹣1（不合题意，舍去）；

当x＜0时，原方程化为x²+x﹣2＝0，解得：x₁＝1，（不合题意，舍去）x₂＝﹣2；

∴原方程的根是x₁＝2，x₂＝﹣2．

请参照例题解方程x²﹣|x﹣1|﹣1＝0．

查看试题解析

四、综合题

23. 某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量y(千克)与每千克降价x(元)(0<x<20)之间满足一次函数关系，其图象如图所示.

(1)、求y与x之间的函数关系式；

(2)、商贸公司要想获利2090元，则这种干果每千克应降价多少元?

查看试题解析
24. 如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm.

(1)、点 P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P、Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由.

(2)、若P点沿射线AB方向从A点出发以1cm/s的速度移动，点 Q沿射线 CB方向从C点出发以2cm/s的速度移动，P、Q同时出发，问几秒后，△PBQ的面积为1cm²？

查看试题解析
25. 阅读理解题：定义：如果一个数的平方等于-1，记为 $i^{2} = - 1$ ①，这个数i叫做虚数单位，那么和我们所学的实数对应起来就叫做复数，复数一般表示为 $a + b i$ （ $a$ ， $b$ 为实数）， $a$ 叫做这个复数的实部， $b$ 叫做这个复数的虚部，它与整式的加法，减法，乘法运算类似．例如：解方程 $x^{2} = - 1$ ，解得： $x_{1} = i$ ， $x_{2} = - i$ ．同样我们也可以化简 $\sqrt{- 4} = \sqrt{4 \times (- 1)} = \sqrt{2^{2} \times i^{2}} = 2 i$ ．读完这段文字，请你解答以下问题：

(1)、填空： $i^{3} =$ ， $i^{4} =$ ， $i^{2} + i^{3} + i^{4} + \cdot \cdot \cdot + i^{2021} =$ ．

(2)、已知 $(a + i) (b + i) = 1 - 3 i$ ，写出一个以 $a$ ， $b$ 的值为解的一元二次方程．

(3)、在复数范围内解方程： $x^{2} - 4 x + 8 = 0$ ．

查看试题解析
26. 某商店准备进一批季节性小家电，单价为每个40元，经市场预测，销售定价为每个52元时，可售出180个，定价每增加1元，销售量净减少10个，定价每减少1元，销售量净增加10个，因受库存的影响，每批次进货个数不超过180个，商店准备获利2000元．

(1)、该商店考虑涨价还是降价？请说明理由．

(2)、应进货多少个？定价为每个多少元？

查看试题解析