2022年浙教版数学八下期中复习阶梯训练：一元二次方程（提高训练）

试卷更新日期：2022-04-03 类型：复习试卷

进入出卷网下载

一、单选题

1. 方程 $x^{2} - 8 x + 15 = 0$ 左边配成一个完全平方式后，所得的方程是（）

A、 ${(x - 6)}^{2} = 1$ B、 ${(x - 4)}^{2} = 1$ C、 ${(x - 4)}^{2} = 31$ D、 ${(x - 4)}^{2} = - 7$

查看试题解析
2. 某农机厂4月份生产零件50万个，第二季度共生产零件182万个.设该厂第二季度平均每月的增长率为x：，那么x满足的方程是（）

A、 $50 {(1 + x)}^{2} = 182$ B、 $50 + 50 (1 + x) + 50 {(1 + x)}^{2} = 182$ C、 $50 (1 + x) + 50 {(1 + x)}^{2} = 182$ D、 $50 + 50 (1 + x) = 182$

查看试题解析
3. 方程 $x^{2} + x - 1 = 0$ 的一个根是（）

A、 $1 - \sqrt{5}$ B、 $\frac{1 - \sqrt{5}}{2}$ C、 $- 1 + \sqrt{5}$ D、 $\frac{\sqrt{5} - 1}{2}$

查看试题解析
4. 若关于 $x$ 的一元二次方程 ${(m - 2)}^{2} x^{2} + (2 m + 1) x + 1 = 0$ 有解，那么 $m$ 的取值范围是（）

A、 $m > \frac{3}{4}$ B、 $m ⩾ \frac{3}{4}$ C、 $m > \frac{3}{4}$ 且 $m \neq 2$ D、 $m ⩾ \frac{3}{4}$ 且 $m \neq 2$

查看试题解析
5. 扬帆中学有一块长30m，宽20m的长方形空地，计划在这块空地上划出四分之一的区域种花，小禹同学的设计方案如图所示，求花带的宽度.设花带的宽度为xm，则可列方程为（）

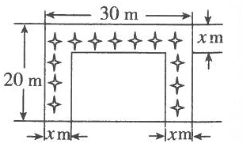A、 $(30 - x) (20 - x) = \frac{3}{4} \times 20 \times 30$ B、 $(30 - 2 x) (20 - x) = \frac{1}{4} \times 20 \times 30$ C、 $30 x + 2 \times 20 x = \frac{1}{4} \times 20 \times 30$ D、 $(30 - 2 x) (20 - x) = \frac{3}{4} \times 20 \times 30$

查看试题解析
6. 已知关于 $x$ 的一元二次方程 $x^{2} + a x - a = 0$ 的一个根是-2，则 $a$ 的值为（）

A、4 B、-4 C、 $\frac{4}{3}$ D、 $- \frac{4}{3}$

查看试题解析
7. 当b+c＝5时，关于x的一元二次方程3x²+bx﹣c＝0的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
8. 已知a是方程x²﹣2x﹣3＝0的一个根，则代数式2a²﹣4a﹣1的值为（）

A、3 B、﹣4 C、3或﹣4 D、5

查看试题解析
9. 现有x支球队参加篮球比赛，比赛采用单循环制即每个球队必须和其余球队比赛一场，共比赛了45场，则下列方程中符合题意的是（）

A、 $\frac{1}{2} x (x - 1) = 45$ B、 $\frac{1}{2} x (x + 1) = 45$ C、x（x﹣1）＝45 D、x（x+1）＝45

查看试题解析
10. 一个三角形两边的长分别是8和6，第三边的长是一元二次方程 $x^{2} - 16 x + 60 - 0$ 的一个实数根，则该三角形的面积是（）

A、24 B、24或 $8 \sqrt{5}$ C、48 D、 $8 \sqrt{5}$

查看试题解析

二、填空题

11. 若关于 $x$ 的一元二次方程 $x^{2} - 6 x + k = 0$ 通过配方法可以化成 ${(x + m)}^{2} = n (n ⩾ 0)$ 的形式，则 $k$ 的值可以是.(写出一个符合要求的 $k$ 值).

查看试题解析
12. 二次项系数为1的一元二次方程的两个根分别为 $1 + \sqrt{2}$ 和 $1 - \sqrt{2}$ ，那么这个方程是.

查看试题解析
13. 在x²＋+4=0的横线上添加一个关于x的一次项，使方程有两个相等的实数根.

查看试题解析
14. 已知直角三角形两条直角边的长分别是方程x²-7x+12=0的两根，则该三角形的斜边长为.

查看试题解析
15. 已知m，n，4分别是等腰三角形(非等边三角形)三边的长，且m，n是关于x的一元二次方程 $x^{2} - 6 x + k + 2 =$ 0的两个根，则 $k$ 的值等于.

查看试题解析
16. 已知：（x²+y²）（x²+y²﹣1）＝20，那么x²+y²＝．

查看试题解析

三、解答题

17. 关于x的方程x²-2.x+2m-1=0有实数根，且m为正整数，求m的值及此时方程的根.

查看试题解析
18. 关于x的一元二次方程 $2 x^{2} + (m - 2) x + 2 = 0$ 有两个相等的实数根，求m的值及方程的根．

查看试题解析
19. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加 $10 %$ ， 5月份的营业额达到633.6万元．求3月份到5月份营业额的平均月增长率．

查看试题解析
20. 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元.假设该公司2~4月每个月生产成本的下降率都相同.请你预测4月份该公司的生产成本.

查看试题解析
21. 用公式法解方程2x²+7x-4=0，并用根与系数的关系检验所求的根是否正确.

查看试题解析
22. 李明将一根长为40cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形.要使这两个正方形的面积之和等于54.5cm² ，那么李明将这根铁丝剪成的两段长度分别是多少？

查看试题解析

四、综合题

23. 某学校于“三八”妇女节期间组织女教师到横店影视城旅游.下面是领队与旅行社导游关于收费标准的一段对话：
【领队】组团去横店影视城旅游每人收费是多少？

【导游】如果人数不超过30人，人均旅游费用为360元.【领队】超过30人怎样优惠呢？

【导游】如果超过30人，每增加1人，人均旅游费用降低5元，但人均旅游费用不得低于300元.该学校按旅行社的收费标准组团游览横店影视城结束后，共支付给旅行社12400元.设该学校这次参加旅游的女教师共有工人.

请你根据上述信息，回答下列问题：

(1)、该学校参加旅游的女教师人数工的取值范围是.

(2)、该学校参加旅游的女教师每人实际应收费元(用含x的代数式表示)

(3)、该学校这次到横店影视城旅游的女教师共有多少人？

查看试题解析
24. 完成下列问题：

(1)、已知x，y为实数，且 $y = 2 \sqrt{x - 5} + 3 \sqrt{5 - x} - 2$ ，求 $2 x - 3 y$ 的值.

(2)、已知 $m$ 是方程 $x^{2} - 2021 x + 1 = 0$ 的一个根，求代数式 $m^{2} - 2020 m + \frac{1}{m} + 2$ 的值.

查看试题解析
25. 已知m，n是方程 $x^{2} - x - 2021 = 0$ 的两个实数根，求下列代数式的值.

(1)、 $m^{2} - m + 2021$ ；

(2)、 $m^{2} - 2 m - n + 2022$ .

查看试题解析