2022年浙教版数学八下期中复习阶梯训练：二次根式（优生集训）

试卷更新日期：2022-04-03 类型：复习试卷

进入出卷网下载

一、综合题

1.

(1)、在Rt△ABC中，∠C＝90°，AC＝2 $\sqrt{2}$ ，AB=3 $\sqrt{2}$ ，求Rt△ABC的周长和面积．

(2)、已知a＝ $\sqrt{3} + \sqrt{2}$ ，b＝ $\sqrt{3} - \sqrt{2}$ ，求a²﹣ab+b²的值．

查看试题解析
2.

(1)、计算 $\sqrt{\frac{2}{3}} - (\frac{1}{6} \sqrt{24} - \frac{3}{2} \sqrt{12})$ (结果保留根号)，并分析其结果在哪两个整数之间；

(2)、已知 $x = 2 - \sqrt{3} ， y = 2 + \sqrt{3}$ ，求代数式 $x^{2} + 2 x y$ $+ y^{2}$ 的值.

查看试题解析
3.

(1)、若 $\sqrt{{(5 - x)}^{2}} = x - 5$ ，则 $x$ 的取值范围是（）

A、 $x < 5$ B、 $x ⩽ 5$ C、 $x ⩾ 5$ D、 $x > 5$

(2)、一个三角形的三边长分别为3，m，5，化简： $\sqrt{4 - 4 m + m^{2}} - \sqrt{m^{2} - 16 m + 64}$ .

(3)、实数a，b在数轴上表示如图，化简：
$\sqrt{{(a + 2)}^{2}} - \sqrt{{(b - 2)}^{2}} + \sqrt{{(a + b)}^{2}}$

查看试题解析
4. 先阅读下列材料，再解决问题：
阅读材料：数学上有一种根号内又带根号的数，它们能通过完全平方公式及二次根式的性质化去一层根号.

例如： $\sqrt{3 + 2 \sqrt{2}} = \sqrt{3 + 2 \times 1 \times \sqrt{2}} = \sqrt{1^{2} + 2 \times 1 \times \sqrt{2} + {(\sqrt{2})}^{2}}$

$= \sqrt{{(1 + \sqrt{2})}^{2}} = | 1 + \sqrt{2} | = 1 + \sqrt{2}$ .

解决问题：化简下列各式

(1)、 $\sqrt{7 + 4 \sqrt{3}}$ ；

(2)、 $\sqrt{9 - 4 \sqrt{5}}$ .

查看试题解析
5. 已知 $\sqrt{m - 10} + 3 \sqrt{10 - m} = n - 6$ .

(1)、求 $m$ 的值；

(2)、求 $m^{2} - n^{2}$ 的平方根.

查看试题解析
6. 若b= $\sqrt{a b - 10} + \sqrt{10 - a b}$ -a+10．

(1)、求ab及a+b的值；

(2)、若a，b满足 $x^{2} - \frac{b}{a} - \frac{a}{b} = 0$ ，试求x的值．

查看试题解析
7. 已知在△ABC中，AB=1，BC= $4 \sqrt{\frac{1}{2}}$ ，CA= $\frac{\sqrt{125}}{5}$

(1)、化简 $4 \sqrt{\frac{1}{2}}$ 和 $\frac{\sqrt{125}}{5}$ ；

(2)、在4×4的方格纸上画出△ABC，使它的顶点都在方格的顶点上(每个小方格的边长均为1)；

(3)、求△ABC最长边上的高的长．

查看试题解析
8. 设a= $\sqrt{8 - x}$ ，b=2，c= $\sqrt{6}$ ．

(1)、当a有意义时，求x的取值范围；

(2)、若a，b，c为直角三角形ABC的三边长，试求x的值．

查看试题解析
9. 已知x= $\frac{1}{2} (\sqrt{7} + \sqrt{5})$ ，y= $\frac{1}{2} (\sqrt{7} - \sqrt{5})$ ，求下列各式的值：

(1)、x²- xy+y² ．

(2)、 $\frac{x}{y} + \frac{y}{x}$

查看试题解析
10.

(1)、 $\sqrt{x^{2} (x - 1)} = x \sqrt{x - 1}$ 成立的条件是

(2)、已知 $\sqrt{\frac{1 - a}{a^{2}}} = \frac{\sqrt{1 - a}}{a}$ ，则a的取值范围是

(3)、已知 $\sqrt{\frac{x - 3}{x + 1}} = \frac{\sqrt{x - 3}}{\sqrt{x + 1}}$ ，则x的取值范围是

查看试题解析
11. 已知p= $\sqrt{{(1 - \sqrt{2})}^{2}} + \sqrt{{(\sqrt{2} - \sqrt{3})}^{2}} + \sqrt{{(\sqrt{3} - \sqrt{4})}^{2}} + ... + \sqrt{{(\sqrt{9} - \sqrt{10})}^{2}}$

(1)、求p的值；

(2)、求证：2< p<3．

查看试题解析
12. 挖掘问题中所隐含的条件，解答下列问题：

(1)、如果 $\sqrt{{(x - 2)}^{2}}$ =2-x，那么（）

A、x<2 B、x≤2 C、x>2 D、x≥2

(2)、已知 $\sqrt{{(x - 3)}^{2}} - {(\sqrt{2 - x})}^{2}$ =2x，求x的值．

(3)、已知a，b是实数，且b> $\sqrt{a - 2}$ -2 $\sqrt{2 - a}$ +1，请化简： $\sqrt{1 - 2 b + b^{2}} - \sqrt{a^{2}}$ ．

查看试题解析
13. 观察下面的变形规律：
$\frac{1}{\sqrt{2} + 1}$ ＝ $\sqrt{2}$ －1， $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\sqrt{3}$ － $\sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}}$ ＝ $\sqrt{4}$ － $\sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}}$ ＝ $\sqrt{5}$ － $\sqrt{4}$ ，…

解答下面的问题：

(1)、若 $n$ 为正整数，请你猜想 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝；

(2)、计算： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2016} + \sqrt{2015}}) \times (\sqrt{2016} + 1)$

查看试题解析
14. 阅读下列解题过程：
$\frac{1}{\sqrt{2} + 1}$ ＝ $\frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)}$ ＝ $\sqrt{2}$ -1；

$\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})}$ ＝ $\sqrt{3}$ - $\sqrt{2}$ ；

$\frac{1}{\sqrt{4} + \sqrt{3}}$ ＝ $\frac{\sqrt{4} - \sqrt{3}}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})}$ ＝ $\sqrt{4}$ - $\sqrt{3}$ ＝2- $\sqrt{3}$ ；

…

解答下列各题：

(1)、 $\frac{1}{\sqrt{10} + \sqrt{9}}$ ＝；

(2)、观察下面的解题过程，请直接写出式子 $\frac{1}{\sqrt{n} - \sqrt{n - 1}}$ ＝．

(3)、利用这一规律计算：（ $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{2021} + \sqrt{2020}}$ ）×（ $\sqrt{2021}$ +1）．

查看试题解析
15. 阅读下列材料，然后解答下列问题：
在进行代数式化简时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：

(一) $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ ；

(二) $\frac{2}{\sqrt{3} + 1} = \frac{2 （ \sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \sqrt{3} - 1$ ；

(三) $\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$ .

以上这种化简的方法叫分母有理化.

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ：
①参照(二)式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝.

②参照(三)式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝__

(2)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots + \frac{1}{\sqrt{99} + \sqrt{97}}$ .

查看试题解析
16. 阅读下面计算过程．
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；

$\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ ．

请解决下列问题

(1)、根据上面的规律，请直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝．

(2)、利用上面的解法，请化简： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \dots + \frac{1}{\sqrt{98} + \sqrt{99}} + \frac{1}{\sqrt{99} + \sqrt{100}}$ ．

(3)、你能根据上面的知识化简 $\frac{1}{\sqrt{n + 1} - \sqrt{n}}$ 吗？若能，请写出化简过程．

查看试题解析
17. 阅读理解：
已知a= $\frac{1}{2 - \sqrt{3}}$ ，求2a²-8a+1的值．

∵a= $\frac{1}{2 - \sqrt{3}}$ = $\frac{2 + \sqrt{3}}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 2 + \sqrt{3}$ ，

∴a-2= $\sqrt{3}$ ．

∴（a-2）²=3，即a²-4a+4=3．

∴a²-4a=-1．

∴2a²-8a+1=2（a²-4a）+1=2×（-1）+1=-1．

请根据以上解答过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1} =$ ．

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \cdot \cdot \cdot + \frac{1}{\sqrt{100} + \sqrt{99}}$ ；

(3)、若a= $\frac{3}{\sqrt{2} + 1}$ ，求2a²+12a-8的值．

查看试题解析
18. 计算：

(1)、 $| 1 - \sqrt{3} | - \sqrt{9} + \sqrt[3]{- 8}$ ；

(2)、直角三角形 $A B C$ 中， $D$ 是斜边 $A B$ 的中，两直角边 $A C = 6$ ， $B C = 8$ ，求 $C D$ 的长．

查看试题解析
19.

(1)、计算： $\sqrt{20} + \sqrt{5} (2 + \sqrt{5})$ ；

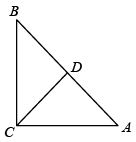(2)、如图，在Rt△ABC中，∠C＝90°，点D是AC上一点，∠BDC＝45°，AB＝13，BC＝5，求AD的长．

查看试题解析
20.

(1)、计算： $\sqrt{27} \times \sqrt{50} \div \sqrt{6}$

(2)、已知 $x = \sqrt{3} - \sqrt{2}$ ， $y = \sqrt{3} + \sqrt{2}$ ，求 $x^{2} - y^{2}$ 的值

查看试题解析
21.

(1)、计算： $\sqrt{24} \times 4 \sqrt{\frac{1}{2}} \div \sqrt{48}$

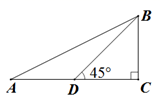(2)、我国古代数学著作《九章算术》中有这样一个问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”意即：一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处．求折断处离地面的高度（注：其中的丈、尺是长度单位，1丈 $= 10$ 尺）

查看试题解析
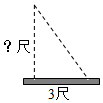22. 解答下列各题：

(1)、计算： $\frac{1}{2} \sqrt{24} - 2 \sqrt{3} \times \sqrt{2} + \sqrt{48} \div \sqrt{2}$

(2)、设实数 $\sqrt{7}$ 的整数部分为a，小数部分为b，求(2a+b)(2a-b)的值.

查看试题解析
23. 阅读下列材料，然后回答问题．在进行二次根式的化简与运算时，我们有时会碰上如 $\frac{5}{\sqrt{3}} ， \sqrt{\frac{2}{3}} ， \frac{2}{\sqrt{3} + 1}$ 一样的式子，其实我们还可以将其进一步化简：
$\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ （一）

$\sqrt{\frac{2}{3}} = \sqrt{\frac{2 \times 3}{3 \times 3}} = \frac{\sqrt{6}}{3}$ （二）

$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$ （三）

以上这种化简的步骤叫做分母有理化．

(1)、请化简： $\frac{2}{\sqrt{3}}$ ＝．

(2)、参照（三）式化简： $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝．

查看试题解析
24. 已知x＝ $\sqrt{3}$ + $\sqrt{2}$ ，y＝ $\sqrt{3}$ ﹣ $\sqrt{2}$ ，求：

(1)、 $x^{2} - y^{2}$ 的值；

(2)、） $\frac{x}{y}$ + $\frac{y}{x}$ 的值．

查看试题解析
25.

(1)、计算： $\frac{3}{4} (\frac{\sqrt{5}}{3} - 2 \sqrt{3}) - \frac{\sqrt{3}}{2} (1 - 4 \sqrt{3} + 3 \sqrt{5})$

(2)、已知 $x + y = 2$ ， $x y = 3$ ，求代数式 $\sqrt{\frac{y}{x}} + \sqrt{\frac{x}{y}}$ 值．

查看试题解析