2021-2022学年初中数学苏科版八年级下册期中考试模拟题

试卷更新日期：2022-04-02 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB＝90°，且BC＝2AD，以AB、BC、DC为边向外作正方形，其面积分别为S₁、S₂、S₃ ，若S₁＝4，S₃＝12，则S₂的值为（）

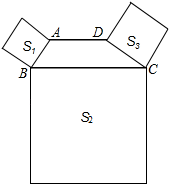A、16 B、24 C、48 D、64

查看试题解析
2. 如图所示，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是（）

A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关

查看试题解析
3. 已知△ABC(如图1)，按图2、图3所示的尺规作图痕迹，不需借助三角形全等，就能推出四边形ABCD是平行四边形的依据是（）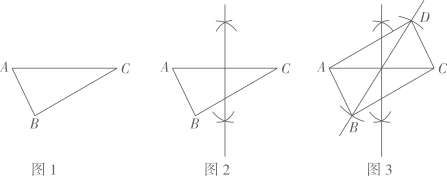

A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形

查看试题解析
4. 下列图形中，既是中心对称图形也是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB＝40°，∠BOC＝30°，则旋转角度是（）

A、10° B、30° C、40° D、70°

查看试题解析
6. 某校为了解学生的出行方式，通过调查制作了如图所示的条形统计图，由图可知，下列说法中错误的是（）

A、步行的人数最少 B、骑自行车的人数为90 C、步行与骑自行车的总人数比乘公共汽车的人数要多 D、乘公共汽车的人数占总人数的50%

查看试题解析
7. 如图，已知平行四边形ABCD的面积为100，P为边CD上的任意一点，E，F分别是线段PA，PB的中点，则图中阴影部分的总面积为（）

A、30 B、25 C、22.5 D、50

查看试题解析
8. 如图，正方形纸片ABCD的四个顶点分别在四条平行线l₁、l₂、l₃、l₄上，这四条直线中相邻两条之间的距离依次为h₁、h₂、h₃（h₁＞0，h₂＞0，h₃＞0），若h₁＝5，h₂＝2，则正方形ABCD的面积S等于（）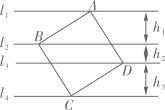

A、34 B、89 C、74 D、109

查看试题解析
9. 下列测量方案中，能确定四边形门框为矩形的是（）

A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量对角线是否相等 D、测量对角线交点到四个顶点的距离是否都相等

查看试题解析
10. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， $A B = \frac{1}{2} B C = 1$ ，则下列结论：①∠CAD=30° ② $B D = \sqrt{7}$ ③S_{平行四边形ABCD}=AB•AC ④ $O E = \frac{1}{4} A D$ ，正确的个数是（）

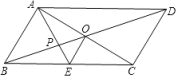A、1 B、2 C、3 D、4

查看试题解析
11. 某学校课外活动小组为了解同学们喜爱的电影类型，设计了如下的调查问卷（不完整）：

准备在“①国产片，②科幻片，③动作片，④喜剧片，⑤亿元大片”中选取三个作为该问题的备选答案，选取合理的是（）

A、①②③ B、①③⑤ C、②③④ D、②④⑤

查看试题解析
12. 如图，电路图上有 $4$ 个开关 $A$ 、 $B$ 、 $C$ 、 $D$ 和 $1$ 个小灯泡，同时闭合开关 $A$ 、 $B$ 或同时闭合开关 $C$ 、 $D$ 都可以使小灯泡发光.下列操作中，“小灯泡发光”这个事件是随机事件的是（）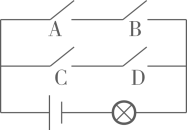

A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关

查看试题解析

二、填空题

13. 如图，在△ABC中，D，E分别为AB，AC的中点，延长DE到点F，使EF=DE，AB=10，BC=8，则四边形BCFD的周长为.

查看试题解析
14. 如图，已知正方形ABCD的边长为6，点E是AB边上一动点，连接ED，将ED绕点E顺时针旋转90°到EF，连接DF，CF，则DF+CF的最小值是．

查看试题解析
15. 某校七年级三个班男生人数与女生人数的比为3：2，各班的男、女学生人数统计图如图所示，则2班的学生人数是.

查看试题解析
16. 如图所示，在矩形ABCD中，AB=2，BC=3，对角线AC的垂直平分线分别交AD，BC于点E，F，连结CE，则CE的长为.

查看试题解析
17. 如图，一个正方形摆放在桌面上，那么这个正方形的边长为．

查看试题解析
18. 某班按课外阅读时间将学生分为3组，第1、2组的频率分别为0.2、0.5，则第3组的频率是 .

查看试题解析

三、综合题

19. 如图，在平行四边形ABCD中，E是BC上的一点，点F在线段DE上，且∠AFE=∠ADC

(1)、若∠AFE=70°，∠DEC=40°，求∠DAF的大小；

(2)、若DE=AD，求证：△AFD≌△DCE

查看试题解析
20. 如图，在四边形ABCD中，∠A=∠ABC=90°，AD=3，BC=5，E是边CD的中点，连结BE并延长与AD的延长线相交于点F，连结CF。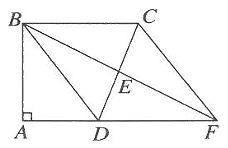

(1)、求证：四边形BDFC是平行四边形；

(2)、若BD=BC，求四边形BDFC的面积。

查看试题解析
21. 如图，在△ABC中，O是AC上的任意一点（不与点A、C重合），过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F.

(1)、OE与OF相等吗？证明你的结论.

(2)、试确定点O的位置，使四边形AECF是矩形，并加以证明.

查看试题解析
22. 如图，已知，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 30 °$ ．将 $△ A B C$ 绕点A逆时针旋转一个 $α$ 角 $(0 ° < α < 180 °)$ 至 $△ A D E$ 位置，连接BD，CE交于点F．

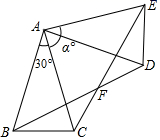(1)、求证： $△ A B D ≌ △ A C E$

(2)、若四边形ABFE为菱形，求 $α$ 的值；

(3)、在（2）的条件下，若 $A B = 2$ ，直接写出CF的值．

查看试题解析
23. 随着通讯技术迅猛发展，人与人之间的沟通方式更多样，更便捷.为此，老师设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种）.某校八年级（1）班同学利用课余时间对全校师生进行了抽样调查，并将统计结果绘制成如图所示两幅不完整的统计图：

请结合图中所给的信息解答下列问题：

(1)、这次参与调查的共有人，在扇形统计图中，表示“微信”的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、如果该校有3600人在使用手机：
①请估计该校最喜欢用“微信”进行沟通的人数；

②在该校师生中随机抽取一人，用频率估计概率，抽取的恰好使用“QQ”的概率是 ▲ .

查看试题解析
24. 如图1，正方形 $A B C D$ 和长方形 $E F G H$ 的周长相等，且各有一条边在数轴上，点 $B ， C ， F ， G$ 对应的数分别是 $- 13 ， - 5 ， 2 ， 8$ ．正方形 $A B C D$ 以每秒2个单位长度的速度向右移动，同时长方形 $E F G H$ 以每秒1个单位长度的速度向左移动．设正方形 $A B C D$ 和长方形 $E F G H$ 重叠部分的面积为S，移动时间为t．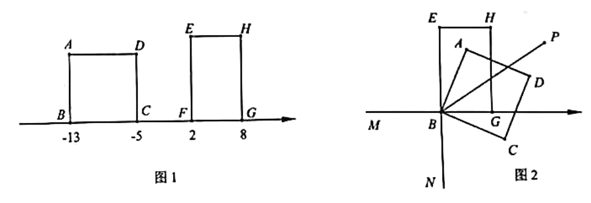

(1)、长方形 $E F G H$ 的面积是．

(2)、当S是长方形 $E F G H$ 面积的一半时，求t的值．

(3)、如图2，当正方形 $A B C D$ 和长方形 $E F G H$ 运动到点B和点F重合时，停止运动，将正方形 $A B C D$ 绕点B顺时针旋转，旋转角度为 $α (0 < α < 180 °)$ ，点 $M 、 N$ 分别在线段 $G B$ 、线段 $E B$ 的延长线上， $B P$ 平分 $∠ C B E$ ，判断 $∠ A B P$ 和 $∠ C B N$ 之间的数量关系，用等式表示，并说明理由．

查看试题解析
25. 在四边形ABCD中，∠A＝∠B＝∠C＝∠D＝90°，AB＝CD＝10，BC＝AD＝8.

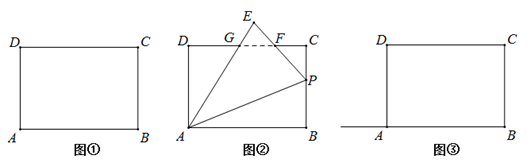(1)、P为BC上一点，将△ABP沿直线AP翻折至△AEP的位置（点B落在点E处）.
①如图①，当点E落在边CD上时，利用尺规作图，在图①中作出满足条件的图形（即△AEP的位置，不写作法，保留作图痕迹），并直接写出此时DE＝ .

②如图②，PE与CD相交于点F，AE与CD相交于点G，且FC＝FE，求BP的长.

(2)、如图③，已知点Q为射线BA上的一个动点，将△BCQ沿CQ翻折，点B恰好落在直线DQ上的点B’处，求BQ的长.

查看试题解析