山东省烟台市芝罘区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-04-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程组中是二元一次方程组的是（）

A、 ${\begin{array}{l} 3 x + 4 y = 6 \\ 5 z - 6 y = 4 \end{array}$ B、 ${\begin{array}{l} x + y = 2 \\ x - y = 4 \end{array}$ C、 ${\begin{array}{l} x + y = 2 \\ x^{2} - y^{2} = 8 \end{array}$ D、 ${\begin{array}{l} x + y = 2 \\ \frac{1}{x} - \frac{1}{y} = \frac{1}{2} \end{array}$

查看试题解析
2. “篮球运动员投篮一次，投中篮筐”这一事件是（）

A、确定事件 B、必然事件 C、不可能事件 D、不确定事件

查看试题解析
3. 下列命题是真命题的是（）

A、两条直线被第三条直线所截，同位角相等 B、在同一平面内，垂直于同一直线的两条直线平行 C、相等的两个角是对顶角 D、三角形的一个外角等于两个内角的和

查看试题解析
4. 如图，在下列条件中，能说明AC∥DE的是（　　）

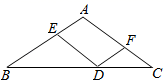A、∠A＝∠CFD B、∠BED＝∠EDF C、∠BED＝∠A D、∠A+∠AFD＝180°

查看试题解析
5. 如图，一个游戏转盘被分成红、黄、蓝三个扇形，其中红、黄扇形的圆心角度数分别为210°，90°，转动转盘，停止后指针落在蓝色区域的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{7}{12}$

查看试题解析
6. 已知 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} 3 x + 2 y = m \\ n x - y = 1 \end{matrix}$ 的解，则m﹣n的值是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 有一个不透明的盒子中装有 $a$ 个除颜色外完全相同的球，这 $a$ 个球中只有3个红球，若每次将球充分搅匀后，任意摸出一个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则 $a$ 的值大约是（）

A、12 B、15 C、18 D、21

查看试题解析
8. 我国古代数学著作《九章算术》卷七有下列问题：“今有共买物，人出八，盈三：人出七，不足四，问人数、物价几何？”意思是：现在有几个人共同出钱去买件物品，如果每人出8钱，则剩余3钱；如果每人出7钱，则差4钱.问有多少人，物品的价格是多少？设有x人，物品的价格为y元，可列方程组为（）

A、 ${\begin{matrix} 8 x - 3 = y \\ 7 x + 4 = y \end{matrix}$ B、 ${\begin{matrix} 8 x + 3 = y \\ 7 x - 4 = y \end{matrix}$ C、 ${\begin{matrix} 8 x = y - 3 \\ 7 x = y - 4 \end{matrix}$ D、 ${\begin{matrix} 8 x = y + 3 \\ 7 x = y + 4 \end{matrix}$

查看试题解析
9. 如图，在△ABC中，AB＝AC＝4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB、AC于M、N，则△AMN的周长为（）

A、4 B、6 C、8 D、10

查看试题解析
10. 如图，在四边形ABCD中，AB∥CD，∠B＝90°，∠DAB与∠ADC的平分线相交于BC边上的M点，则下列结论：①∠AMD＝90°；②点M为BC的中点；③AB+CD＝AD；④△ADM的面积是梯形ABCD面积的一半．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，宽为 $50 c m$ 的长方形图案是由10个相同的小长方形拼成的，则其中一个小长方形的面积为（）

A、 $400 c m^{2}$ B、 $500 c m^{2}$ C、 $600 c m^{2}$ D、 $800 c m^{2}$

查看试题解析
12. 一次长跑中，当小明跑了1600米时，小刚跑了1400米，小明、小刚在此后所跑的路程y(米)与时间t(秒)之是的函数关系如图，则这次长跑的全程为（）米.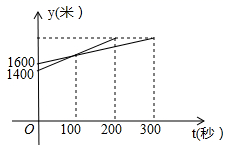

A、2000米 B、2100米 C、2200米 D、2400米

查看试题解析

二、填空题

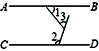
13. 将命题“同角的补角相等”写成“如果......那么.....”的形式：．

查看试题解析
14. 如图，AB∥CD，∠1=50°，∠2=110°，则∠3=度．

查看试题解析
15.
如图，已知函数y＝ax+b和y＝kx的图象交于点P ，则根据图象可得，关于x ， y的二元一次方程组 $\{\begin{matrix} y = a x + b \\ y = k x \end{matrix}$ 的解是．

查看试题解析
16. 已知（a+2b﹣3）²+|2a+3b﹣2|＝0，则（a+b）²⁰²¹＝．

查看试题解析
17. 如图，由4个直角边分别是1和2的直角三角形拼成一个“弦图”地面，在该地面上任意抛一颗豆子（豆子大小不记），豆子恰好落在中间灰色区域的概率是．

查看试题解析
18. 关于x，y的二元一次方程组 ${\begin{array}{l} x + 2 y = 3 \\ 4 x - y = k \end{array}$ 的解满足x﹣y＝﹣2，则k的值是．

查看试题解析
19. 一副直角三角尺如图叠放，现将含有30°的三角尺ABC固定不动，将含有45°的三角尺ADE绕点A顺时针旋转一个锐角α，使DE∥BC，则α的度数为．

查看试题解析
20. 如图a是长方形纸带，∠DEF＝20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数．

查看试题解析

三、解答题

21. 解方程组： ${\begin{array}{l} 3 x + 2 y = 6 \\ 2 x - \frac{1}{2} y = 4 \end{array}$ ．

查看试题解析
22. 小明和小亮两位同学做掷骰子（质地均匀的正方体）游戏，他们共做了100次试验，结果如下：
朝上的点数
1
2
3
4
5
6
出现的次数
15
14
25
20
13
13

(1)、计算“1点朝上”的频率和“6点朝上”的频率；

(2)、小明说：“根据试验，一次试验中出现3点朝上的概率最大．”小亮说：“若投掷1000次，则出现4点朝上的次数正好是200次．”小明和小亮的说法符合题意吗？为什么？

(3)、小明将一枚骰子任意投掷一次，求朝上的点数不小于4的概率．

查看试题解析
23. 如图，点F在线段AB上，点E，G在线段CD上，FG∥AE，∠1＝∠2．

(1)、求证：AB∥CD；

(2)、若FG⊥BC于点H，DC＝DB，∠D＝100°，求∠1的度数．

查看试题解析
24. 我校组织一批学生开展社会实践活动，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满.已知45座客车租金为每辆220元，60座客车租金为每辆300元.

(1)、这批学生的人数是多少？原计划租用45座客车多少辆？

(2)、若租用同一种客车，要使每位学生都有座位，应该怎样租用合算？

查看试题解析
25. 阅读下列材料：
小明同学遇到下列问题：解方程组 ${\begin{array}{l} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{array}$ 小明发现如果用代入消元法或加减消元法求解，运算量比较大，容易出错．如果把方程组中的（2x+3y）看成一个整体，把（2x﹣3y）看成一个整体，通过换元，可以解决问题．以下是他的解题过程：令m＝2x+3y，n＝2x﹣3y．原方程组化为 ${\begin{array}{l} \frac{m}{4} + \frac{n}{3} = 7 \\ \frac{m}{3} + \frac{n}{2} = 8 \end{array}$ ，解的 ${\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ ，把 ${\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ 代入m＝2x+3y，n＝2x﹣3y，得 ${\begin{array}{l} 2 x + 3 y = 60 \\ 2 x - 3 y = - 24 \end{array}$ 解得 ${\begin{array}{l} x = 9 \\ y = 14 \end{array}$ 所以，原方程组的解为 ${\begin{array}{l} x = 9 \\ y = 14 \end{array}$ ．
请你参考小明同学的做法解方程组：

(1)、 ${\begin{array}{l} \frac{x + y}{6} + \frac{x - y}{10} = 3 \\ \frac{x + y}{6} - \frac{x - y}{10} = - 1 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{5}{x} + \frac{2}{y} = 11 \\ \frac{3}{x} - \frac{2}{y} = 13 \end{array}$ ．

查看试题解析
26. 问题情境：
如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°．求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线性质，可得∠APC＝∠APE+∠CPE＝50°+60°＝110°．
问题解决：

(1)、如图2，AB∥CD，直线l分别与AB、CD交于点M、N，点P在直线I上运动，当点P在线段MN上运动时（不与点M、N重合），∠PAB＝α，∠PCD＝β，判断∠APC、α、β之间的数量关系并说明理由；

(2)、在（1）的条件下，如果点P在线段MN或NM的延长线上运动时．请直接写出∠APC、α、B之间的数量关系；

(3)、如图3，AB∥CD，点P是AB、CD之间的一点（点P在点A、C右侧），连接PA、PC，∠BAP和∠DCP的平分线交于点Q．若∠APC＝116°，请结合（2）中的规律，求∠AQC的度数．

查看试题解析
27. 如图，Rt△ABC，∠ACB＝90°，AC＝BC，已知点A和点C的坐标分别为（0，2）和（﹣1，0），过点A、B的直线关系式为y＝kx+b．

(1)、求点B的坐标和直线AB的函数关系式；

(2)、在第二象限y＝kx+b的图象上是否存在点P，使△ACP的面积为4？若存在；请求出符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析

朝上的点数	1	2	3	4	5	6
出现的次数	15	14	25	20	13	13