山东省烟台市龙口市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-04-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列事件中，是确定事件的是（）

A、三角形任意两边之和小于第三边 B、365人中一定至少有两人的生日相同 C、龙口市下周一定会下雨 D、打开电视机，正在播放广告

查看试题解析
2. 已知正数m的平方根是3x﹣2和5x+6，则m的值是（）

A、﹣ $\frac{1}{2}$ B、 $\frac{7}{2}$ C、 $\frac{49}{4}$ D、﹣ $\frac{7}{2}$

查看试题解析
3. 如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含45°角的直角三角板的斜边与纸条一边重合，含30°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（）

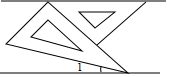A、10° B、15° C、20° D、25°

查看试题解析
4. 甲、乙、丙、丁四支足球队进行小组单循环比赛（每两队都要比赛一场），结果甲队胜了丙队，并且甲、乙、丁胜的场数相同，则这三队各胜的场数是（）

A、3 B、2 C、1 D、0

查看试题解析
5. 如图，四边形ABCD中，∠A＝90°，∠C＝110°，点E，F分别在AB，BC上，将△BEF沿EF翻折，得△GEF，若GF∥CD，GE∥AD，则∠D的度数为（）

A、60° B、70° C、80° D、90°

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ，点 $D$ 在 $A B$ 上， $A D = A C$ ， $A F ⊥ C D$ 交 $C D$ 于点 $E$ ，交 $C B$ 于点 $F$ ，则 $C F$ 的长是（）

A、1.5 B、1.8 C、2 D、2.5

查看试题解析
7. 在一个不透明的布袋中装有60个白球和若干个黑球，除颜色外其他都相同，小红每次摸出一个球并放回，通过多次试验后发现，摸到黑球的频率稳定在0.6左右，则布袋中黑球的个数可能有（）

A、24 B、36 C、40 D、90

查看试题解析
8. 汉代数学家赵爽在注解（周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝，如图所示的弦图中，四个直角三角形都是全等的，它们的两直角边分别是2和3．现随机向该图形内掷一枚飞镖，则飞镖落在小正方形内（非阴影区域）的概率为（）

A、1 B、 $\frac{12}{13}$ C、 $\frac{1}{12}$ D、 $\frac{1}{13}$

查看试题解析

二、填空题

9. $\sqrt{16}$ 的算术平方根是

查看试题解析
10. 已知关于x，y的方程组 ${\begin{array}{l} 3 x + 2 y = 2 k \\ 5 x + 4 y = 3 k - 5 \end{array}$ 与方程x+y=3k的解相同，则k的值为．

查看试题解析
11. 如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线l₁ ， l₂ ， l₃上，且l₁ ， l₂之间的距离为1，l₂ ， l₃之间的距离为2，则AC的长是．

查看试题解析
12. 如图，直线y=x+1与直线y=mx-n相交于点M(1，b)，则关于x，y的方程组 ${\begin{array}{l} x + 1 ＝ y \\ m x - y ＝ n \end{array}$ 的解为：.

查看试题解析
13. 如图，△ABC中，AD⊥BC于点D，∠BAD＝ $\frac{1}{2}$ ∠CAD，BE平分∠ABC交AC于E，∠C＝42°，若点F为线段BC上的一点，当△EFC为直角三角形时，∠BEF的度数为．

查看试题解析
14. 长方形ABCD中放置了6个形状、大小都相同的小长方形，所标尺寸如图所示，则图中阴影部分的面积是cm² ．

查看试题解析

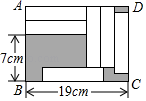
三、解答题

15. 若方程组 ${\begin{array}{l} \frac{2 x - y}{3} - 2 y = 6 \\ 2 (2 x + y) = 1 - \frac{3}{2} y \end{array}$ 的解满足方程2ax﹣3by＝26．求正整数a，b的值

查看试题解析
16. 在一个不透明的袋子中装有仅颜色不同的20个小球，其中红球6个，黑球14个

(1)、先从袋子中取出x（x＞3）个红球后，再从袋子中随机摸出1个球，将“摸出黑球”，记为事件A．请完成下列表格．
事件A
必然事件
随机事件
x的值

(2)、先从袋子中取出m个红球，再放入2m个一样的黑球并摇匀，随机摸出1个球是黑球的概率是 $\frac{11}{12}$ ，求m的值．

查看试题解析
17. 如图，已知∠DAE+∠CBF =180°，CE 平分∠BCD，∠BCD =2∠E．

(1)、求证：AD//BC；

(2)、CD 与 EF 平行吗？写出证明过程；

(3)、若 DF 平分∠ADC，求证CE⊥DF．

查看试题解析
18. 垫球是排球队常规训练的重要项目之一．训练课上，甲、乙、丙三人相互之间进行垫球练习，每个人的球都等可能的传给其他两人，球最先从甲手中传出，共进行两次垫球

(1)、请列举出两次传球的所有等可能情况；

(2)、求两次传球后，球回到甲手中的概率；

(3)、两次传球后，球传到乙手中的概率大还是传到丙手中的概率大？请说明理由．

查看试题解析

19. 网络商店（简称网店）是近年来迅速兴起的一种电子商务形式，小明的网店销售红枣、小米两种商品的相关信息如下表：

商品	红枣	小米
规格	1kg/袋	2kg/袋
成本（元/袋）	40	38
售价（元/袋）	60	54

根据上表提供的信息，解答下列问题

(1)、已知今年前四个月，小明的网店销售上表中规格的红枣和小米共2000kg ，获得利润2.8万元，求这前四个月小明的网店销售这种规格的红枣和小米各多少袋？

(2)、根据之前的销售情况，估计今年5月到12月这后八个月，小明的网店还能销售同规格的红枣和小米共4000kg ，其中，红枣的销售量不低于1200kg ．假设这后八个月，销售红枣x（kg），销售红枣和小米获得的总利润为y（元），求出y与x之间的函数关系式，并求出这后八个月，小明的网店销售这种规格的红枣和小米至少获得总利润多少元？

查看试题解析

20. 已知点D，E，F分别是△ABC的边AB，AC，BC上的点，DE∥BC，DF∥AC．

(1)、如图1，点G是线段FD延长线上一点，连接EG，∠CEG的平分线EM交AB于点M，交FD于点N．则∠A，∠AME，∠CEG之间存在怎样的数量关系？请写出证明过程；

(2)、如图2，在（1）的条件下，若EG平分∠AED，∠AME＝35°，且∠EDF﹣∠A＝30°，求∠C的度数．

查看试题解析
21. 已知线段AB⊥直线l于点B，点D在直线l上，分别以AB，AD为边作等边三角形ABC和等边三角形ADE，直线CE交直线l于点F．

(1)、当点F在线段BD上时，如图1，线段DF，CE，CF之间的数量关系是；

(2)、当点F在线段DB的延长线上时，如图2．
①（1）中的数量关系是否仍然成立？若成立，请写出证明过程；若不成立，请重新写出正确的结论，并写出证明过程；
②若△ABC和△ADE的边长分别是 $\sqrt{3}$ 和 $\sqrt{7}$ ， DF=3，求BE的长．

查看试题解析

事件A	必然事件	随机事件
x的值