山东省泰安市新泰市2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-04-02 类型:期中考试
一、单选题
-
1. 下列是二元一次方程的是( )A、 B、 C、 D、2. 已知 是方程 的一个解,那么 的值是( )A、-2 B、2 C、-4 D、43. 如图,直线a、b被直线c所截,下列条件能使a//b的是( )
 A、 B、 C、 D、4. 下列选项中,假命题是( )A、对顶角相等 B、相等的角是对顶角 C、两点之间,线段最短 D、邻补角互补5. 如图,已知直线 .直角三角板 的直角顶点C在直线b上,若 ,则 ( )
A、 B、 C、 D、4. 下列选项中,假命题是( )A、对顶角相等 B、相等的角是对顶角 C、两点之间,线段最短 D、邻补角互补5. 如图,已知直线 .直角三角板 的直角顶点C在直线b上,若 ,则 ( ) A、 B、 C、 D、6. 《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问:甲、乙持钱各几何?”大意是:甲、乙二人带着钱,不知是多少,若甲得到乙的钱线数的 , 则甲的钱数为50,若乙得到甲的钱数的 , 则乙的钱数也能为50.问甲、乙各有多少钱?设甲有钱为x,乙有钱为y,可列方程组为( )A、 B、 C、 D、7. 以下事件中:①两个奇数的乘积是奇数;②抛掷一枚均匀的骰子,朝上点数为2;③每天太阳从东边升起;④明天要下雨:⑤长分别为2,3,4的三条线段能围成一个三角形.是必然事件的有( )A、5个 B、4个 C、3个 D、2个8. 二元一次方程 有一组解互为相反数,则y的值为( )A、2 B、1 C、0 D、-19. 利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.量的数据如图,则桌子的高度等于( )
A、 B、 C、 D、6. 《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,问:甲、乙持钱各几何?”大意是:甲、乙二人带着钱,不知是多少,若甲得到乙的钱线数的 , 则甲的钱数为50,若乙得到甲的钱数的 , 则乙的钱数也能为50.问甲、乙各有多少钱?设甲有钱为x,乙有钱为y,可列方程组为( )A、 B、 C、 D、7. 以下事件中:①两个奇数的乘积是奇数;②抛掷一枚均匀的骰子,朝上点数为2;③每天太阳从东边升起;④明天要下雨:⑤长分别为2,3,4的三条线段能围成一个三角形.是必然事件的有( )A、5个 B、4个 C、3个 D、2个8. 二元一次方程 有一组解互为相反数,则y的值为( )A、2 B、1 C、0 D、-19. 利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.量的数据如图,则桌子的高度等于( )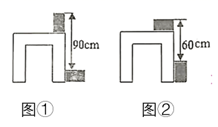 A、 B、 C、 D、10. 从这六个数中随机抽取一个数,恰好为负数的概率为( )A、 B、 C、 D、11. 如图,已知一次函数的图象与轴,轴分别交于点 , , 与正比例函数交于点 , 已知点的横坐标为2,以下结论:①关于的方程的解为:②对于直线 , 当时,:③对于直线 , 当时,:④方程组的解为 , 其中正确的有( )个
A、 B、 C、 D、10. 从这六个数中随机抽取一个数,恰好为负数的概率为( )A、 B、 C、 D、11. 如图,已知一次函数的图象与轴,轴分别交于点 , , 与正比例函数交于点 , 已知点的横坐标为2,以下结论:①关于的方程的解为:②对于直线 , 当时,:③对于直线 , 当时,:④方程组的解为 , 其中正确的有( )个 A、1 B、2 C、3 D、412. 如图, 的角平分线 、 相交于 , , ,且 于 ,下列结论:① ;② ;③ 平分 ;④ .其中正确的结论的个数是( ).
A、1 B、2 C、3 D、412. 如图, 的角平分线 、 相交于 , , ,且 于 ,下列结论:① ;② ;③ 平分 ;④ .其中正确的结论的个数是( ).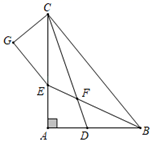 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
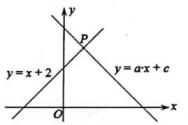
13. 以下成语:①守株待兔;②瓮中捉鳖;③百步穿杨;④水中捞月.所描述的事件中是不可能事件的是(填序号).14. 把方程 改写成用含 的式子表示 的形式是:.15. 如图,直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m,3),则方程组 的解为。
 16. 小明家的客厅地板如图所示,一个小球在地板上任意滚动,并随机停留在某块地板砖上,每块地板砖的大小质地完全相同,那么小球停留在黑色区域的概率是 .
16. 小明家的客厅地板如图所示,一个小球在地板上任意滚动,并随机停留在某块地板砖上,每块地板砖的大小质地完全相同,那么小球停留在黑色区域的概率是 . 17. 如图, ,且CF平分∠AFE , 若 ,则∠A的度数是 .
17. 如图, ,且CF平分∠AFE , 若 ,则∠A的度数是 .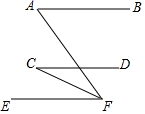 18. 如图, 是 的平分线, 是 的平分线, 与 交于 ,若 , ,则 .
18. 如图, 是 的平分线, 是 的平分线, 与 交于 ,若 , ,则 .
三、解答题
-
19. 解下列方程(组):(1)、(2)、20. “五·一”期间,某书城为了招徕顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元图书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.
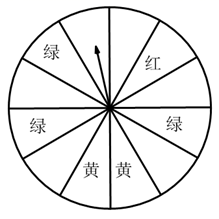 (1)、写出任意转动一次转盘获得购书券的概率;(2)、写出任意转动一次转盘获得45元,30元,25元的概率.21. 如图,已知是直线上的一点,平分 , 射线 ,
(1)、写出任意转动一次转盘获得购书券的概率;(2)、写出任意转动一次转盘获得45元,30元,25元的概率.21. 如图,已知是直线上的一点,平分 , 射线 , (1)、求的度数;(2)、若 , 求证:;22. 已知一个不透明的袋中装有除颜色外完全相同的9个黄球,6个黑球,3个红球.(1)、求从袋中任意摸出一个球是红球的概率;(2)、若要使摸到红球的概率为 , 则需要在这个口袋中再放入多少个红球?23. 已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C.
(1)、求的度数;(2)、若 , 求证:;22. 已知一个不透明的袋中装有除颜色外完全相同的9个黄球,6个黑球,3个红球.(1)、求从袋中任意摸出一个球是红球的概率;(2)、若要使摸到红球的概率为 , 则需要在这个口袋中再放入多少个红球?23. 已知,如图,EF⊥AC于F,DB⊥AC于M,∠1=∠2,∠3=∠C. (1)、求证:AB//MN.(2)、若∠C=40°,∠MND=100°,求∠CAD的度数.24. 春节即将来临,抗击新冠疫情防控工作至关重要,某公司加紧生产酒精消毒液与额温枪两种抗疫物质,其两种物资的生产成本和销售单价如表所示:
(1)、求证:AB//MN.(2)、若∠C=40°,∠MND=100°,求∠CAD的度数.24. 春节即将来临,抗击新冠疫情防控工作至关重要,某公司加紧生产酒精消毒液与额温枪两种抗疫物质,其两种物资的生产成本和销售单价如表所示:种类
生产成本(元/件)
销售单价(元/件)
酒精消毒液
56
62
额温枪
84
100
(1)、若该公司2020年12月生产两种物资共100万件,生产总成本为7280万元,请用列二元一次方程组的方法,求该月酒精消毒液和额温枪两种物资各生产了多少万件?(2)、该公司2021年1月生产两种物资共150万件,根据市场需求,该月将举办迎新年促销活动,其中酒精消毒液的销售单价降低2元,额温枪打9折销售.若设该月生产酒精消毒液x万件,该月销售完这两种物资的总利润为y万元,求y与x之间的函数关系式.25. △ABC中,AD是∠BAC的角平分线,AE是△ABC的高.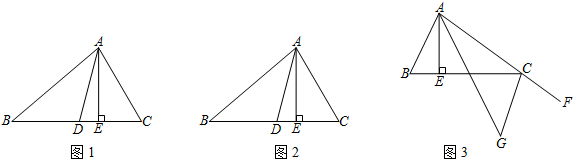 (1)、如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;(2)、如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;(3)、如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
(1)、如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;(2)、如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;(3)、如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .