山东省泰安市岱岳区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-04-02 类型:期中考试
一、单选题
-
1. 方程 , , , , 中,二元一次方程的个数是( )A、5个 B、4个 C、3个 D、2个2. 下列语句中,假命题的是( )A、垂线段最短 B、如果直线a、b、c满足a∥b , b∥c , 那么a∥c C、同角的余角相等 D、如果∠AOB=80°,∠BOC=20°,那么∠AOC=60°3. 如图,直线 , 直线分别交、于点、 , 直线交于点 . 若 , , 则度数等于( )
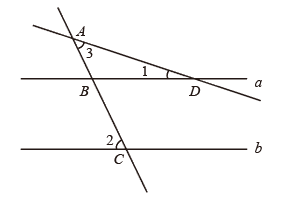 A、30° B、45° C、60° D、85°4. 已知是二元一次方程组的解,则的值为( )A、 B、 C、3 D、45. 投掷一枚质地均匀的硬币4次,其中3次正面向上,1次反面向上,则第5次掷出反面向上的概率为( )A、 B、 C、 D、6. 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A、30° B、45° C、60° D、85°4. 已知是二元一次方程组的解,则的值为( )A、 B、 C、3 D、45. 投掷一枚质地均匀的硬币4次,其中3次正面向上,1次反面向上,则第5次掷出反面向上的概率为( )A、 B、 C、 D、6. 如图,如果AB∥EF,EF∥CD,下列各式正确的是( ) A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°7. 现用190张铁皮做盒子,每张铁皮做8个盒身或做22个盒底,而一个盒身与两个盒底配成一个盒子,设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )A、 B、 C、 D、8. 在不透明的袋子里装有颜色不同的10个红球和若干个白球,每次从袋子里摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,估计袋中白球有( )个A、15个 B、20个 C、26个 D、21个9. 如图,下列不能判定DF∥AC的条件是( )
A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°7. 现用190张铁皮做盒子,每张铁皮做8个盒身或做22个盒底,而一个盒身与两个盒底配成一个盒子,设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )A、 B、 C、 D、8. 在不透明的袋子里装有颜色不同的10个红球和若干个白球,每次从袋子里摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,估计袋中白球有( )个A、15个 B、20个 C、26个 D、21个9. 如图,下列不能判定DF∥AC的条件是( ) A、∠A=∠BDF B、∠2=∠4 C、∠1=∠3 D、∠A+∠ADF=180°10. 下列试验中,①抛掷一枚质地均匀的硬币,结果出现“正面朝上”与出现“反面朝上”;②在三张相同的小纸条上分别标上1,2,3这3个号码,做成3支签放在一个盒子中,搅匀后从中抽到“1号签”,“2号签”,3号签”,③一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中摸出“红球”与“白球”,试验是结果具有等可能性的有( )A、0个 B、1个 C、2个 D、3个11. 用图象法解二元一次方程组时,小英所画图象如图所示,则方程组的解为( )
A、∠A=∠BDF B、∠2=∠4 C、∠1=∠3 D、∠A+∠ADF=180°10. 下列试验中,①抛掷一枚质地均匀的硬币,结果出现“正面朝上”与出现“反面朝上”;②在三张相同的小纸条上分别标上1,2,3这3个号码,做成3支签放在一个盒子中,搅匀后从中抽到“1号签”,“2号签”,3号签”,③一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中摸出“红球”与“白球”,试验是结果具有等可能性的有( )A、0个 B、1个 C、2个 D、3个11. 用图象法解二元一次方程组时,小英所画图象如图所示,则方程组的解为( ) A、 B、 C、 D、12. 如图,将 沿 翻折,使其顶点 均落在点O处,若 ,则 的度数为( )
A、 B、 C、 D、12. 如图,将 沿 翻折,使其顶点 均落在点O处,若 ,则 的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知直线y=x+b和y=ax﹣3交于点P(2,1),则关于x的方程x+b=ax﹣3的解为 .14. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
 15. “若a2=b2 , 则a=b”这一事件是.(填“必然事件”“不可能事件”或“随机事件”)16. 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC=.
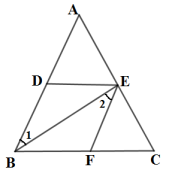
15. “若a2=b2 , 则a=b”这一事件是.(填“必然事件”“不可能事件”或“随机事件”)16. 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC=. 17. 在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色球共20只.其中,黑球6只试估算口袋中再加入黑球只,才能使摸出黑球的概率是 ?18. 如图,在中, , 与的平分线交于点 , 得;与的平分线相交于点 , 得;;与的平分线相交于点 , 得 , 则 .
17. 在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色球共20只.其中,黑球6只试估算口袋中再加入黑球只,才能使摸出黑球的概率是 ?18. 如图,在中, , 与的平分线交于点 , 得;与的平分线相交于点 , 得;;与的平分线相交于点 , 得 , 则 .
三、解答题
-
19. 按要求解方程组:(1)、;(2)、;(3)、 .20. 如图,DE∥BC,∠ADE=∠EFC,那么∠1与∠2相等吗?说明理由.
 21. 在一个口袋中装有4个红球和8个白球,它们除颜色外完全相同.(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件,并写出其发生的概率;(2)、求从口袋中随机摸出一个球是红球的概率;;(3)、现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,要使从中随机摸出一个球是红球的概率是 ,问取走了多少个白球?22. 如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
21. 在一个口袋中装有4个红球和8个白球,它们除颜色外完全相同.(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件,并写出其发生的概率;(2)、求从口袋中随机摸出一个球是红球的概率;;(3)、现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,要使从中随机摸出一个球是红球的概率是 ,问取走了多少个白球?22. 如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°. (1)、请你判断∠1与∠BDC的数量关系,并说明理由;(2)、若∠1=70°,DA平分∠BDC,试求∠FAB的度数.23. 随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.(1)、打折前甲、乙两种品牌粽子每盒分别为多少元?(2)、阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
(1)、请你判断∠1与∠BDC的数量关系,并说明理由;(2)、若∠1=70°,DA平分∠BDC,试求∠FAB的度数.23. 随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.(1)、打折前甲、乙两种品牌粽子每盒分别为多少元?(2)、阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?

