山东省济南市历城区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-04-02 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，直线b、c被直线a所截，则 $∠ 1$ 与 $∠ 2$ 是（）

A、对顶角 B、同位角 C、内错角 D、同旁内角

查看试题解析
2. 世界最大的单口径球面射电望远镜被誉为“中国天眼”，在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒．数据0.00519用科学记数法可以表示为（）

A、5.19×10^﹣3 B、5.19×10^﹣4 C、5.19×10^﹣5 D、5.19×10^﹣6

查看试题解析
3. 用下列长度的三根木棒首尾相接，能做成三角形框架的是（）

A、1，2，3 B、1，1，2 C、1，2，2 D、1，5，7

查看试题解析
4. 下列运算正确的是（）

A、x⁸÷x⁴＝x⁴ B、（a+1）²＝a²+a+1 C、3（a³）²＝6a⁶ D、x³•x²＝x⁶

查看试题解析
5. 若一个三角形的三个内角度数的比为2：3：4，则这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
6. 如图，如果 $∠ 1 = ∠ 2$ ，那么下面结论正确的是（）

A、 $A D / / B C$ B、 $A B / / C D$ C、 $∠ 3 = ∠ 4$ D、 $∠ A = ∠ C$

查看试题解析
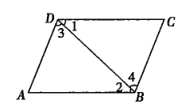7. 如图，已知AB∥DE ， ∠1＝30°，∠2＝35°，则∠BCE的度数为（）

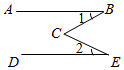A、70° B、65° C、35° D、5°

查看试题解析
8. 如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中正确的是（）

A、△ABC中，AD是BC边上的高 B、△ABC中，GC是BC边上的高 C、△GBC中，CF是BC边上的高 D、△GBC中，GC是BG边上的高

查看试题解析
9. 如图为了测量B点到河对面的目标A之间的距离，在B点同侧选择了一点C，测得∠ABC＝65°，∠ACB＝35°，然后在M处立了标杆，使∠MBC＝65°，∠MCB＝35°，得到△MBC≌△ABC，所以测得MB的长就是A，B两点间的距离，这里判定△MBC≌△ABC的理由是（）

A、SAS B、AAA C、SSS D、ASA

查看试题解析
10. 如图，测量运动员跳远成绩选取的是AB的长度，其依据是（）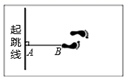

A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、两点之间直线最短

查看试题解析
11. 如图，在△ACB中，∠ACB=90°，∠A=24°，D是AB上一点．将△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′的度数为（）

A、42° B、40° C、30° D、24°

查看试题解析
12. 如图1，有一正方形广场ABCD，图形中的线段均表示直行道路， $\overset{⌢}{B D}$ 表示一条以A为圆心，以AB为半径的圆弧形道路．如图2，在该广场的A处有一路灯，O是灯泡，夜晚小齐同学沿广场道路散步时，影子长度随行走路线的变化而变化，设他步行的路程为x （m）时，相应影子的长度为y （m），根据他步行的路线得到y与x之间关系的大致图象如图3，则他行走的路线是（）

A、A→B→E→G B、A→E→D→C C、A→E→B→F D、A→B→D→C

查看试题解析

二、填空题

13. 已知 $∠ A = 45 °$ ，则 $∠ A$ 的补角是．

查看试题解析
14. 已知3^x=5，3^y=2，则3^x+y的值是.

查看试题解析
15. 如图所示的网格是正方形网格，A，B，C，D是网格交点，则 $△$ ABC的面积与 $△$ ABD的面积的大小关系为： $S_{△ A B C}$ $S_{△ A B D}$ （填“＞”，“＝”或“＜”）

查看试题解析
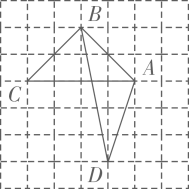16. 如图，已知∠ABC＝∠DCB，要使△ABC≌△DCB，根据“SAS”判定方法，需要再添加的一个条件是．

查看试题解析
17. 如图，若BO、CO分别是∠ABC、∠ACB的三等分线，也就是∠OBC＝ $\frac{1}{3}$ ∠ABC，∠OCB＝ $\frac{1}{3}$ ∠ACB，∠A＝72°，则∠BOC＝°．

查看试题解析
18. 如图，D、E分别是△ABC边AB、BC上的点，AD＝3BD，BE＝CE，设△ADF的面积为S₁ ， △CEF的面积为S₂ ，若S_△ABC＝8，则S₁﹣S₂的值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $(π - 3)^{0} - 2^{2} + (\frac{1}{2})^{- 3}$ ；

(2)、（﹣2x²）³+x⁴•x²；

(3)、（5x²y﹣10xy²）÷5xy；

(4)、（a﹣b）²+b（a﹣b）；

(5)、124×122﹣123²（用乘法公式计算）．

查看试题解析
20. 先化简，再求值已知x＝1，y＝﹣2，求多项式[（2x﹣y）（2x+y）﹣y（6x﹣y）]÷2x的值．

查看试题解析
21. 探究：如图1，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F，若∠ABC＝50°，求∠DEF的度数．
请将下面的解答过程补充完整，并填空
解：∵DE∥BC
∴∠DEF＝                  ▲                   ．（                  ▲                  ）
∵EF∥AB，
∴ ＝∠ABC．（                  ▲                  ）
∴∠DEF＝∠ABC．（等量代换）
∵∠ABC＝50°，
∴∠DEF＝                  ▲                   ．
应用：如图2，直线AB，BC，AC两两相交，交点分别为A、B、C，点D在线段AB的延长线上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F，若∠ABC＝65°，则∠DEF＝                  ▲                   ．

查看试题解析
22. 如图，点B，E，C，F在一条直线上，AB＝DF，AC＝DE，BE＝CF．求证：∠A＝∠D．

查看试题解析
23. 为了解某品牌轿车的耗油情况，将油箱加满后进行了耗油试验，得到如表数据：
轿车行驶的路程s（km）
0
10
20
30
40
…
油箱剩余油量w（L）
50
49.2
48.4
47.6
46.8
…

(1)、在这个变化过程中，自变量是，因变量是；

(2)、该轿车油箱的容量为 L，行驶50km时，油箱剩余油量为L．

(3)、根据如表的数据，写出油箱剩余油量w（L）与轿车行驶的路程s（km）之间的表达式．

查看试题解析
24. 甲、乙两名同学骑自行车从A地出发沿同一条路前往B地，他们离A地的距离s（km）与甲离开A地的时间t（h）之间的关系图象如图所示，根据图象提供的信息，回答下列问题：

(1)、A地与B的路程是km；

(2)、同学先到达B地；提前了h；

(3)、乙的骑行速度是km/h；

(4)、甲从A地到B地的平均速度是 km/h．

查看试题解析
25. 问题背景：
在学习了完全平方公式后，老师布置了一道作业题：如图，长方形ABCD的长为a，宽为b，面积为4，周长为10，分别以a，b为边作正方形ABEF及ADGH，求两个正方形面积之和．小燕同学认真思考后，发现利用现有知识不能求出a，b的值，但可以用完全平方公式通过适当的变形求a²+b²的值，从而求得两个正方形面积之和．

(1)、问题解决：请你依据上述内容填写已知条件和结果：
a+b＝， ab＝， a²+b²＝．

(2)、已知x+y＝7，xy＝10，求（x﹣y）²的值．

查看试题解析
26. 已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作等边△ADE（顶点A、D、E按逆时针方向排列），连接CE．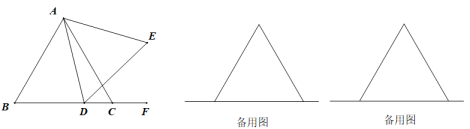

(1)、如图，当点D在边BC上时，求证：①△ABD≌△ACE，②AC＝CE+CD；

(2)、当点D不在边BC上时，其他条件不变，请写出AC、CE、CD之间存在的数量关系．

查看试题解析

轿车行驶的路程s（km）	0	10	20	30	40	…
油箱剩余油量w（L）	50	49.2	48.4	47.6	46.8	…