山东省济南市济阳区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-04-02 类型:期中考试
一、单选题
-
1. 地表以下岩层的温度随着所处深度的变化而变化,在这一问题中自变量是( )A、地表 B、岩层的温度 C、所处深度 D、时间2. 2020年1月24日,中国疾控中心成功分离我国首株新型冠状病毒毒种,该毒种直径大约为80纳米(1纳米=0.000001毫米),数据“80纳米”用科学记数法表示为( )A、毫米 B、毫米 C、毫米 D、毫米3. 计算: 的结果是( )A、 B、 C、 D、4. 下列各图中,∠1与∠2是对顶角的是( )A、
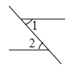 B、
B、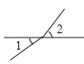 C、
C、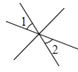 D、
D、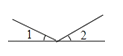 5. 下列能用平方差公式计算的是( )A、 B、 C、 D、6. 如果的乘积中不含x的一次项,则a为( )A、5 B、-5 C、 D、7. 如图,将一张矩形纸片折叠,若 , 则的度数是( )
5. 下列能用平方差公式计算的是( )A、 B、 C、 D、6. 如果的乘积中不含x的一次项,则a为( )A、5 B、-5 C、 D、7. 如图,将一张矩形纸片折叠,若 , 则的度数是( ) A、 B、 C、 D、8. 如图,是某蓄水池的横断面示意图,分深水区和浅水区,如果向这个蓄水池以固定的流量注水,图中哪个图像能大致表示水的最大深度和时间之间的函数关系( )
A、 B、 C、 D、8. 如图,是某蓄水池的横断面示意图,分深水区和浅水区,如果向这个蓄水池以固定的流量注水,图中哪个图像能大致表示水的最大深度和时间之间的函数关系( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 计算的结果是A、2 B、 C、 D、110. 将温度计从热茶的杯子中取出之后,立即被放入一杯凉水中.每隔后读一次温度计上显示的度数,将记录下的数据制成下表:
9. 计算的结果是A、2 B、 C、 D、110. 将温度计从热茶的杯子中取出之后,立即被放入一杯凉水中.每隔后读一次温度计上显示的度数,将记录下的数据制成下表:时间t(单位:s)
5
10
15
20
25
30
温度计读数(单位:℃)
49.0
31.0
22.0
16.5
14.0
12.0
下述说法不正确的是( )
A、自变量是时间,因变量是温度计的读数 B、当时,温度计上的读数是31.0℃ C、温度计的读数随着时间推移逐渐减小,最后保持不变 D、依据表格中反映出的规律,时,温度计上的读数是13.0℃11. 某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行,已知第一次转过的角度,第三次转过的角度,则第二次拐弯角 的度数是( ) A、 B、 C、 D、12. 如图,两个正方形的边长分别为a,b,如果 , 则阴影部分的面积为( )
A、 B、 C、 D、12. 如图,两个正方形的边长分别为a,b,如果 , 则阴影部分的面积为( ) A、9 B、6 C、3 D、12
A、9 B、6 C、3 D、12二、填空题
-
13. 计算:x(x﹣3)= .14. 若是完全平方式,则k的值为 .15. 如图所示,两个直角三角形的直角顶点重合,如果 ,那么 .
 16. 若 , ,则 .17. 按如图所示的程序计算函数y的值,若输入的x值为﹣3,则输出y的结果为 .
16. 若 , ,则 .17. 按如图所示的程序计算函数y的值,若输入的x值为﹣3,则输出y的结果为 . 18. 我国宋朝数学家杨辉在他的著作《详解九章算术》中提出下表,此表揭示了(n为非负整数)展开式的各项系数的规律,例如:
18. 我国宋朝数学家杨辉在他的著作《详解九章算术》中提出下表,此表揭示了(n为非负整数)展开式的各项系数的规律,例如:(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2 , 它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3 , 它有四项,系数分别为1,3,3,1;…
根据以上规律,(a+b)6展开式共有项,各项系数的和等于 .

三、解答题
-
19. 计算:20. 在括号中填写理由.如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°( ▲ )
∴AB∥CD ( ▲ )
∴∠B= ▲ ( ▲ )
又∵∠B=∠D(已知 ),
∴∠D= ▲ ( ▲ )
∴AD∥BE( ▲ )
∴∠E=∠DFE( ▲ )
21. 一个角的补角是这个角的余角的3倍,求这个角的度数.22. 先化简,再求值:[(2x+y)2-y(y+4x)-8xy]÷(2x),其中x=2,y=-1.23. 已知,如图直线AB与CD相交于点O,∠BOE=90°,∠AOD=30°,OF为∠BOD的角平分线.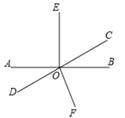 (1)、求∠EOC度数;(2)、求∠EOF的度数.24. 如图,一个长方形中剪下两个大小相同的正方形(有关线段的长如图所示),留下一个“T”型的图形(阴影部分)
(1)、求∠EOC度数;(2)、求∠EOF的度数.24. 如图,一个长方形中剪下两个大小相同的正方形(有关线段的长如图所示),留下一个“T”型的图形(阴影部分) (1)、用含x,y的代数式表示“T”型图形的面积并化简.(2)、若米,米,“T”型区域铺上价格为每平方米20元的草坪,请计算草坪的造价.25. 文具店出售书包和文具盒,书包每个定价为30元,文具盒每个定价为5元.该店制定了两种优惠方案:①买一个书包赠送一个文具盒;②按总价的九折(总价的90%)付款.某班学生需购买8个书包、若干个文具盒(不少于8个),如果设文具盒个数为x(个),付款数为y(元).(1)、分别求出两种优惠方案中y与x之间的关系式;(2)、购买文具盒多少个时,两种方案付款相同?26. 一辆汽车油箱内有油a升,从某地出发,每行驶1小时耗油6升,若设剩余油量为Q升,行驶时间为t/小时,根据以上信息回答下列问题:
(1)、用含x,y的代数式表示“T”型图形的面积并化简.(2)、若米,米,“T”型区域铺上价格为每平方米20元的草坪,请计算草坪的造价.25. 文具店出售书包和文具盒,书包每个定价为30元,文具盒每个定价为5元.该店制定了两种优惠方案:①买一个书包赠送一个文具盒;②按总价的九折(总价的90%)付款.某班学生需购买8个书包、若干个文具盒(不少于8个),如果设文具盒个数为x(个),付款数为y(元).(1)、分别求出两种优惠方案中y与x之间的关系式;(2)、购买文具盒多少个时,两种方案付款相同?26. 一辆汽车油箱内有油a升,从某地出发,每行驶1小时耗油6升,若设剩余油量为Q升,行驶时间为t/小时,根据以上信息回答下列问题: (1)、开始时,汽车的油量a=升;(2)、在行驶了小时汽车加油,加了升,写出加油前Q与t之间的关系式;(3)、当这辆汽车行驶了9小时,剩余油量多少升?27. 以直线上一点O为端点作射线 , 使 , 将一个直角角板的直角顶点放在O处,即 .
(1)、开始时,汽车的油量a=升;(2)、在行驶了小时汽车加油,加了升,写出加油前Q与t之间的关系式;(3)、当这辆汽车行驶了9小时,剩余油量多少升?27. 以直线上一点O为端点作射线 , 使 , 将一个直角角板的直角顶点放在O处,即 . (1)、如上图1,若直角三角板的一边放在射线上,则;(2)、如上图2,将直角三角板绕点O顺时针转动到某个位置,
(1)、如上图1,若直角三角板的一边放在射线上,则;(2)、如上图2,将直角三角板绕点O顺时针转动到某个位置,①若恰好平分 , 则 ▲ ;
②若在内部,请直接写出与有怎样的数量关系;
(3)、将直角三角板绕点O顺时针转动(与重合时为停止)的过程中,恰好有 , 求此时的度数.