山东省德州市庆云县2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-04-02 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{49}$ 的平方根是（）

A、7 B、﹣7 C、 $\pm \sqrt{7}$ D、 $\pm \sqrt{49}$

查看试题解析
2. 在平面直角坐标系中，点P（－3，4）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3.
如图所示，在图形B到图形A的变化过程中，下列描述正确的是（　　）

A、向上平移2个单位，向左平移4个单位 B、向上平移1个单位，向左平移4个单位 C、向上平移2个单位，向左平移5个单位 D、向上平移1个单位，向左平移5个单位

查看试题解析
4. 下列各数：2π， $\frac{17}{5}$ ， $\sqrt{24}$ ， 0.333333， $\sqrt{64}$ ， 1.21221222122221……（每两个1之间依次多一个2），3.14， $2 - \sqrt{2}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 下列生活中的实例，可以用“两点之间线段最短”来解释的是（）

A、把一根木条固定到墙上需要两颗钉子 B、从一条河道能向集镇引一条最短的水渠 C、小狗看到远处的食物，总是径直奔向食物 D、经过刨平木板上的两个点，能弹出一条笔直的墨线

查看试题解析
6. 已知 $\sqrt{a + 2}$ +|b﹣1|＝0，那么 ${(a + b)}^{2021}$ 的值为（）

A、﹣1 B、1 C、2021 D、﹣2021

查看试题解析
7. 估计 $\sqrt{10} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
8. 如图，按各组角的位置判断不正确的是（）

A、∠1与∠4是同旁内角 B、∠3与∠4是内错角 C、∠5与∠6是同旁内角 D、∠2与∠5是同位角

查看试题解析
9. 下列语句中，假命题的是（　　）

A、对顶角相等 B、若直线a、b、c满足b∥a，c∥a，那么b∥c C、两直线平行，同旁内角互补 D、互补的角是邻补角

查看试题解析
10.
如图，∠1=∠2，则下列结论一定成立的是（　　）

A、AB//CD B、AD//BC C、∠B=∠D D、∠3=∠4

查看试题解析
11. 如图，∠1＝70°，直线a平移后得到直线b，则∠2－∠3（）

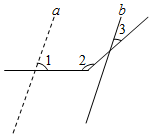A、70° B、180° C、110° D、80°

查看试题解析
12. 在平面直角坐标系xOy中，对于点P（x，y）我们把点P（﹣y+1，x+1）叫做点P伴随点.已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， ….若点A₁的坐标为（2，4），点A₂₀₂₁的坐标为（）

A、（﹣3，3） B、（﹣2，﹣2） C、（3，﹣1） D、（2，4）

查看试题解析

二、填空题

13. 若 $(2 a + 3)^{2} + \sqrt{b - 2} = 0$ 则 $\sqrt{a^{b}} =$ .

查看试题解析
14. 在平面直角坐标系中，点P（a，a+1）在x轴上，那么点P的坐标是．

查看试题解析
15. 如图，直线 $a / / b$ ，将三角尺的直角顶点放在直线b上，若 $∠ 1 = 35 °$ ，则 $∠ 2$ 等于

查看试题解析
16. 已知 $\sqrt{23}$ 的整数部分为a，小数部分为b，则a-b=.

查看试题解析
17. 如图，若AD∥BE，且∠ACB＝90°，∠CBE＝30°，则∠CAD＝度．

查看试题解析
18. 观察下列各式：(1) $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}}$ ，(2) $\sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}}$ ，(3) $\sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ，…，请用你发现的规律写出第8个式子是.

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{25} - \sqrt[3]{- 64} + | 1 - \sqrt{2} |$ ；

(2)、解方程：3（x﹣1）²=12．

查看试题解析
20. 如图，方格纸中每个小方格都是边长为1个单位长度的正方形，已知三角形ABC的顶点在格点上，在建立平面直角坐标系后，A的坐标为（2，－4），B的坐标为（5，－4），C的坐标为（4，－1）．

(1)、画出三角形ABC；

(2)、求三角形ABC的面积；

(3)、若把三角形ABC向上平移2个单位长度，再向左平移4个单位长度得到三角形A′B′C′，在图中画出三角A′B′C′，并写出B′的坐标．

查看试题解析
21. 已知 $a$ ， $b$ 满足 $| a - 4 | + \sqrt{b - 7}$ =0，解关于 $x$ 的方程 $(a - 3) x^{2} - 1 = 5 b$ ．

查看试题解析
22. 如图，在四边形ABCD中，∠D＝100°，CA平分∠BCD，且∠ACB＝40°，∠BAC＝70°．

(1)、AD与BC平行吗？试写出推理过程．

(2)、若点E在线段BA的延长线上，求∠DAC和∠EAD的度数．

查看试题解析
23. 我们知道 $\sqrt{2}$ 是无理数，其整数部分是1，于是小明用 $\sqrt{2}$ －1来表示 $\sqrt{2}$ 的小数部分．
请解答下列问题：

(1)、 $\sqrt{10}$ 的整数部分是，小数部分是．

(2)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求a＋b－ $\sqrt{5}$ 的值；

(3)、已知10＋ $\sqrt{3}$ ＝x＋y，其中x是整数，且0＜y＜1，求x－y的相反数．

查看试题解析
24. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足 $\sqrt{a - 4}$ +|b﹣6|=0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动．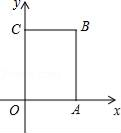

(1)、a= ， b= ，点B的坐标为；

(2)、当点P移动4秒时，请指出点P的位置，并求出点P的坐标；

(3)、在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．

查看试题解析
25.

(1)、问题发现
如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C＝∠BEC．
请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC（已知），EF∥AB（辅助线的作法），
∴EF∥DC（                  ▲                  ）
∴∠C＝∠CEF．（                  ▲                  ）
∵EF∥AB，∴∠B＝∠BEF（同理），
∴∠B+∠C＝                  ▲                  (等量代换）
即∠B+∠C＝∠BEC．

(2)、拓展探究
如果点E运动到图②所示的位置，其他条件不变，求证：∠B+∠C＝360°﹣∠BEC．

(3)、解决问题
如图③，AB∥DC，∠C＝120°，∠AEC＝80°，则∠A＝．（之间写出结论，不用写计算过程）

查看试题解析