山东省滨州市滨城区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-04-02 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示，∠1和∠2是对顶角的图形是（）

A、 B、 C、 D、

查看试题解析
2. 如图，某单位要在河岸l上建一个水泵房引水到C处，他们的做法是：过点C作CD⊥l于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是（）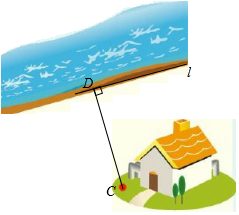

A、两点之间，线段最短 B、在同一平面内，过一点有且只有一条直线与已知直线垂直 C、两点确定一条直线 D、直线外一点与直线上所有点的连线中，垂线段最短

查看试题解析
3. 点 $A (- 1 ， \sqrt{2})$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4.
如图，点P是直线a外的一点，点A、B、C在直线a上，且PB⊥a，垂足是B，PA⊥PC，则下列不正确的语句是（　　）

A、线段PB的长是点P到直线a的距离 B、PA、PB、PC三条线段中，PB最短 C、线段AC的长是点A到直线PC的距离 D、线段PC的长是点C到直线PA的距离

查看试题解析
5. 在下列各数中是无理数的有（）0.3030030003， $\sqrt{4}$ ， $\sqrt{5}$ ， ﹣ $\sqrt[3]{3}$ ， $\frac{π}{3}$ ， $\frac{22}{7}$ ， 3.14，2.010101…（相邻两个1之间有1个0），9.0123456…（小数部分由相继的正整数组成）．

A、3个 B、4个 C、5个 D、6个

查看试题解析
6. 下列所示的四个图形中，∠1和∠2是同位角的是（）

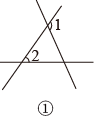
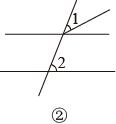
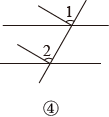A、②③ B、①②③ C、③④ D、①②④

查看试题解析
7. 如图，点E在射线AB上，要AD $/ /$ BC，只需（）

A、∠A=∠CBE B、∠A=∠C C、∠C=∠CBE D、∠A+∠D= 180°

查看试题解析
8. 将点A（﹣2，3）通过以下哪种方式的平移，得到点A'（﹣5，7）（）

A、沿x轴向右平移3个单位长度，再沿y轴向上平移4个单位长度 B、沿x轴向左平移3个单位长度，再沿y轴向下平移4个单位长度 C、沿x轴向左平移4个单位长度，再沿y轴向上平移3个单位长度 D、沿x轴向左平移3个单位长度，再沿y轴向上平移4个单位长度

查看试题解析
9. 若一个自然数的算术平方根是a，则比这个自然数大4的自然数的算术平方根是（）

A、a+2 B、a²+4 C、a+4 D、 $\sqrt{a^{2} + 4}$

查看试题解析
10. 下列命题是真命题的（）

A、无理数的相反数是有理数 B、如果ab＞0，那么a＞0，b＞0 C、内错角相等，两直线平行 D、若|a|＝1，则a＝1

查看试题解析
11. 如图，表示 $- \sqrt{7}$ 的点落在（）

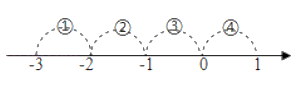A、段① B、段② C、段③ D、段④

查看试题解析
12. 如图，在平面直角坐标系中，OA₁＝1，将边长为1的正方形一边与x轴重合按图中规律摆放，其中相邻两个正方形的间距都是1，则点A₂₀₂₂的坐标为（）

A、（1009，1） B、（1010，1） C、（1011，0） D、（1011，﹣1）

查看试题解析

二、填空题

13. 如图，直线a，b相交于点O，若 $∠ 1 + ∠ 2 = 220 °$ ，则 $∠ 3 =$ ．

查看试题解析
14. 把命题“对顶角相等”改写成“如果⋯那么⋯”的形式，正确的改写应为．

查看试题解析
15. $3 a - 22$ 和 $2 a - 3$ 都是 $m$ 的平方根，则 $m$ 的值为．

查看试题解析
16. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是．

查看试题解析
17. 比较大小： $\frac{\sqrt{5} - 1}{2}$ 0.6（填“＞”或“＜”）．

查看试题解析
18. 在平面直角坐标系中，A点的坐标为（ $2$ ， $- 1$ ），若线段 $A B$ ∥x轴，且 $A B = 3$ ，则点B的坐标为．

查看试题解析
19. 给出表格：

a

0.0001

0.01

1

100

10000

$\sqrt{a}$

0.01

0.1

1

10

100

利用表格中的规律计算：已知 $\sqrt{15}$ =k， $\sqrt{0.15}$ =a， $\sqrt{1500}$ =b，则a+b= ． (用含k的代数式表示)

查看试题解析
20. 直线AB、CD相交于点O ， ∠AOC＝30°，若OE⊥AB ， OF平分∠DOE ，则∠COF的度数为．

查看试题解析

三、解答题

21. 求下列各式中的x值：

(1)、4x²﹣12＝0

(2)、x³﹣3＝ $\frac{3}{8}$

(3)、 $- (- 2)^{2} + \sqrt{16} - \sqrt[3]{27}$

(4)、 $- 2^{2} \times {(\frac{1}{2})}^{2} + | 3 - π | + \sqrt[3]{- 64} \div | - 2 |$

查看试题解析
22. 如图，在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知三角形 $A B C$ 的顶点 $A$ 的坐标为 $A (- 1 ， 4)$ ，顶点 $B$ 的坐标为 $(- 4 ， 3)$ ，顶点 $C$ 的坐标为 $(- 3 ， 1)$ .

(1)、把三角形 $A B C$ 向右平移5个单位长度，再向下平移4个单位长度得到三角形 $A^{'} B^{'} C^{'}$ ，请你画出三角形 $A^{'} B^{'} C^{'}$ ；

(2)、请直接写出点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(3)、求三角形 $A B^{'} C$ 的面积.

查看试题解析
23. 如图，∠AFD＝∠1，AC∥DE ．

(1)、试说明：DF∥BC；

(2)、若∠1＝70°，DF平分∠ADE ，求∠B的度数．

查看试题解析
24. 如图，D，E分别在△ABC的边AB，AC上，F在线段CD上，且∠1+∠2＝180°，DE//BC．

(1)、求证：∠3＝∠B；

(2)、若DE平分∠ADC，∠2＝3∠B，求∠1的度数．

查看试题解析
25. 化简．

(1)、 $\sqrt{2^{2}}$ ＝， $\sqrt{(- 2)^{2}}$ ＝， $\sqrt{0}$ ＝， $\sqrt{a^{2}}$ ＝．

(2)、 $\sqrt[3]{3^{3}}$ ＝， $\sqrt[3]{(- 3)^{3}}$ ＝． $\sqrt[3]{0}$ ＝， $\sqrt[3]{a^{3}}$ ＝．

(3)、根据以上信息，观察a，b所在位置，完成化简， ${(\sqrt{b})}^{2}$ + $\sqrt{(b - a)^{2}}$ ﹣ $\sqrt[3]{(a - b)^{3}}$

查看试题解析
26. 如图1，已知AB//CD，P是直线AB，CD外的一点，PF⊥CD于点F，PE交AB于点E，满足∠FPE＝60°．

(1)、求∠AEP的度数；

(2)、如图2，射线PN从PE出发，以每秒10°的速度绕P点按逆时针方向匀速旋转，当PN到达PF时立刻返回至PE，然后继续按上述方式旋转；射线EM从EA出发，以相同的速度绕E点按顺时针方向旋转至EP后停止运动，此时射线PN也停止运动．若射线PN、射线EM同时开始运动，设运动时间为t秒．
①当射线PN平分∠EPF时，求∠MEP的度数（0°＜∠MEP＜180°）；
②当直线EM与直线PN相交所成的锐角是60°时，则t＝ ▲ ．

查看试题解析

a	0.0001	0.01	1	100	10000
$\sqrt{a}$	0.01	0.1	1	10	100