广东省茂名市电白区2020-2021学年高二下学期数学期中考试试卷
试卷更新日期:2022-04-02 类型:期中考试
一、单选题
-
1. 若z-3+5i=8-2i,则等于( )A、8-7i B、5-3i C、11-7i D、8+7i2. 甲、乙、丙三人排成一排去照相,甲不站在排头的所有排列种数为( )A、6 B、4 C、8 D、103. 若复数为纯虚数,则它的共轭复数是( )A、 B、 C、 D、4. 一辆汽车按规律做直线运动,若汽车在时的瞬时速度为4,则( )A、 B、 C、2 D、35. 某大街在甲、乙、丙三处设有红、绿灯,汽车在这三处因遇绿灯而通行的概率分别为 , 则汽车仅在甲处因遇红灯而停车一次的概率为( )A、 B、 C、 D、6. 据统计,在某次联考中,考生数学单科分数服从正态分布 , 考生共10000人,任选一考生数学单科分数在分的概率为( )附:若随机变呈服从正态分布 , 则A、 B、 C、27. D、7. 函数 的图像在点 处的切线方程为( )A、 B、 C、 D、8. 围棋起源于中国,据先秦典籍世本记载:“尧造围棋,丹朱善之”,至今已有四千多年历史围棋不仅能抒发意境、陶冶情操、修身养性、生慧增智,而且还与天象易理、兵法策略、治国安邦等相关联,蕴含着中华文化的丰富内涵在某次国际围棋比赛中,甲、乙两人进入最后决赛比赛采取五局三胜制,即先胜三局的一方获得比赛冠军,比赛结束假设每局比赛甲胜乙的概率都为 , 没有和局,且各局比赛的胜负互不影响,则甲在比赛中以获得冠军的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列结论正确的是( )A、 B、 C、若 , 则 D、10. 下列说法正确的是( )A、设有一个回归方程 , 变量增加一个单位时,平均增加5个单位; B、若两个具有线性相关关系的变量的相关性越强,则线性相关系数的值越接近于1 C、在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高 D、在线性回归模型中,相关指数越接近于1,说明回归的效果越好11. 已知函数 , 其导函数的图象经过点 , 如图所示,则下列说法中正确的是( )
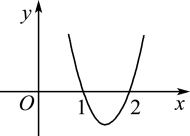 A、当时,函数取得最小值; B、在上单调递增; C、当时,函数取得极小值; D、当时,函数取得极大值.12. 设函数 ,则下列说法正确的是( )A、 定义域是(0,+ ) B、x∈(0,1)时, 图象位于x轴下方 C、 存在单调递增区间 D、 有且仅有两个极值点
A、当时,函数取得最小值; B、在上单调递增; C、当时,函数取得极小值; D、当时,函数取得极大值.12. 设函数 ,则下列说法正确的是( )A、 定义域是(0,+ ) B、x∈(0,1)时, 图象位于x轴下方 C、 存在单调递增区间 D、 有且仅有两个极值点三、填空题
-
13. 在 的展开式中, 的系数为.(用数字作答)14. 在复平面内,若 , 对应的复数分别为 , , 则.15. 已知随机变量 , 则(用数字作答).16. 设函数f(x)=ex+ae−x(a为常数).若f(x)为奇函数,则a=;若f(x)是R上的增函数,则a的取值范围是 .
四、解答题
-
17. 某一射手射击所得环数的分布列如下:
5
6
7
8
9
10
0.06
0.18
0.22
0.18
0.12
(1)、求的值;(2)、求此射手射击所得环数的数学期望.18. 中华人民共和国道路交通安全法第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,中华人民共和国道路交通安全法第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:月份
1
2
3
4
5
违章驾驶人数
120
105
100
90
85
参考公式:
(1)、请利用所给数据求违章人数与月份之间的回归直线方程(2)、预测该路口7月份的不“礼让斑马线”违章驾驶员人数.19. 学校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加省举办的“我看中国改革开放三十年"演讲比赛活动.(1)、设“男生甲被选中”为事件A,"女生乙被选中”为事件B,求和;(2)、设所选3人中男生人数为 , 求的分布列和数学期望.20. 在某市高三数学质量检测中,全市共有5000名学生参加了本次考试,其中示范性高中参加考试学生人数为2000人,非示范性高中参加考试学生人数为3000人.现从所有参加考试的学生中随机抽取100人,做检测成绩数据分析.
参考公式
参考数据:
(1)、依据100人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;(2)、如果规定成绩不低于130分为特别优秀,现已知语文特别优秀占样本人数的5%,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有99%的把握认为语文特别优秀的同学与数学也特别优秀有关.语文特别优秀
语文不特别优秀
合计
数学特别优秀
数学不特别优秀
合计