2021-2022学年浙教版七年级下册期中复习专题5二元一次方程综合（精英卷）

试卷更新日期：2022-04-01 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列以 ${\begin{cases} x = 2 \\ y = - 1 \end{cases}$ 为解的二元一次方程组是（）

A、 ${\begin{cases} 3 x + y = 5 \\ 2 x + 3 y = 7 \end{cases}$ B、 ${\begin{cases} 3 x + y = - 5 \\ 2 x - 3 y = 7 \end{cases}$ C、 ${\begin{cases} 3 x + y = 5 \\ 2 x - 3 y = 7 \end{cases}$ D、 ${\begin{cases} 3 x + y = - 5 \\ 2 x - 3 y = - 7 \end{cases}$

查看试题解析
2. 下列方程：①x+y=1；②2x- $\frac{y}{2}$ =1；③x²+y²=1；④5（x+y）=7（x-y）；⑤x²=1；⑥x+ $\frac{1}{2}$ =4，其中是二元一次方程的是（）

A、① B、①③ C、①②④ D、①②④⑥

查看试题解析
3. 若方程组 ${\begin{array}{l} 2 x - y = 1 ， \\ 3 x + 2 y = 12 \end{array}$ 的解也是二元一次方程 $5 x - m y = - 11$ 的一个解，则 $m$ 的值应等于（）

A、5 B、-7 C、-5 D、7

查看试题解析
4. 某车间每天能生产甲种零件120个或者乙种零件100个.3个甲种零件与2个乙种零件配成一套，要在27天内生产最多的成套产品，问甲、乙两种零件各生产几天？设甲种零件生产 $x$ 天，乙种零件生产 $y$ 天，下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 27 \\ 120 x = 100 y \end{array}$ B、 ${\begin{array}{l} x + y = 27 \\ 2 \times 120 x = 3 \times 100 y \end{array}$ C、 ${\begin{array}{l} x + y = 27 \\ 3 \times 120 x = 2 \times 100 y \end{array}$ D、 ${\begin{array}{l} x + y = 27 \\ 2 x = 3 y \end{array}$

查看试题解析
5. 已知方程组 ${\begin{array}{l} x + 2 y = 4 \\ 2 x + y = k \end{array}$ 的解满足 $x + y = 1$ ，则 $k$ 的值为（）

A、7 B、 $- 7$ C、1 D、 $- 1$

查看试题解析
6. 在沙县国际连锁早餐店里，李大爷买5个馒头、3个包子，老板少拿2元，只要17元；张大妈买11个馒头、5个包子，老板以售价的九折优惠，只要33.3元．若馒头每个 $x$ 元，包子每个 $y$ 元，依题意可列方程组为（）

A、 ${\begin{array}{l} 5 x + 3 y = 17 + 2 \\ 11 x + 5 y = 33.3 \times 0.9 \end{array}$ B、 ${\begin{array}{l} 5 x + 3 y = 17 + 2 \\ 11 x + 5 y = 33.3 \div 0.9 \end{array}$ C、 ${\begin{array}{l} 5 x + 3 y = 17 - 2 \\ 11 x + 5 y = 33.3 \times 0.9 \end{array}$ D、 ${\begin{array}{l} 5 x + 3 y = 17 - 2 \\ 11 x + 5 y = 33.3 \div 0.9 \end{array}$

查看试题解析
7. 设“■▲●”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，则“？”处应该放“●”（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 某校举行篮球赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分.八年级一班在16场比赛中得26分.设该班胜x场，负y场，则根据题意，下列方程组中正确的是（）

A、 ${\begin{array}{l} x + y = 26 \\ x + 2 y = 16 \end{array}$ B、 ${\begin{array}{l} x + y = 26 \\ 2 x + y = 16 \end{array}$ C、 ${\begin{array}{l} x + y = 16 \\ x + 2 y = 26 \end{array}$ D、 ${\begin{array}{l} x + y = 16 \\ 2 x + y = 26 \end{array}$

查看试题解析
9. 如果 ${\begin{cases} x + 2 y - 8 z = 0 \\ 2 x - 3 y + 5 z = 0 \end{cases}$ ，其中xyz≠0，那么x：y：z=（）

A、1：2：3 B、2：3：4 C、2：3：1 D、3：2：1

查看试题解析
10. 小明在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形如图1；小红看见了，说：“我也来试一试．”结果小红七拼八凑，拼成了如图2那样的正方形，中间还留下了一个洞，恰好是面积为 $9 c m^{2}$ 的小正方形，则每个小长方形的面积为（）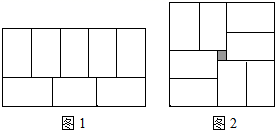

A、135cm² B、108cm² C、68cm² D、60cm²

查看试题解析

二、填空题

11. 一副三角板按如图所示的方式摆放，且 $∠ 1$ 的度数是∠2的3倍，则∠2的度数为．

查看试题解析
12. 若x^|a|-1+（a-2）y=1是关于x，y的二元一次方程，则a=.

查看试题解析
13. 在y= $\frac{2}{3}$ x-4中，如果x=6，那么y=；如果y=-2，那么x=.

查看试题解析
14. 在一本书上写着方程组 ${\begin{array}{l} x + p y = 0 ， \\ x + y = 1 \end{array}$ 的解是 ${\begin{array}{l} x = 0.5 ， \\ y = Δ ， \end{array}$ 其中 $y$ 的值被墨渍盖住了，不过仍能求出 $p =$ .

查看试题解析
15. 为了保护环境，某校环保小组成员小明收集废电池，第一天收集1号电池4节，5号电池5节，总质量为460克；第二天收集1号电池2节，5号电池3节，总质量为240克，则1号电池每节重为克，5号电池每节重为克.

查看试题解析
16. 三个同学对问题“若方程组 ${\begin{cases} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{cases}$ 的解是 ${\begin{cases} x = 3 \\ y = 4 \end{cases}$ ，求方程组 ${\begin{cases} 3 a_{1} (x - 1) + b_{1} (y + 3) = 4 c_{1} \\ 3 a_{2} (x - 1) + b_{2} (y + 3) = 4 c_{2} \end{cases}$ 的解。”提出各自的想法。
甲说：“这个题目的好象条件不够，不能求解”；

乙说：“它们的系数有一定的规律，可以试试”；

丙说：“能不能把第二个方程组的两个方程的两边都除以4，通过换元替代的方法来解决”，

参考他们的讨论，你能求出这个方程组的解吗？x=.y=

查看试题解析

三、计算题

17. 解下列方程组：

(1)、 ${\begin{array}{l} y = x - 1 \\ 4 x + 3 y = 11 \end{array}$

(2)、 ${\begin{array}{l} 2 x + 3 y = - 6 \\ 3 x - 2 y = 4 \end{array}$

查看试题解析
18. 解下列方程（组）

(1)、 $\frac{2 x + 5}{3} - \frac{3 x - 2}{4} =$ 1.

(2)、 ${\begin{array}{l} 2 x - 3 y = 7 \\ x + 3 y = - 1 \end{array}$ .

查看试题解析

四、解答题

19. 已知关于x，y的方程组 ${\begin{array}{l} 3 x + 5 y = 3 a \\ - x - 3 y = 12 \end{array}$ ，若该方程组的解x，y的值互为相反数，求a的值和方程组的解.

查看试题解析
20. 学习了一次方程后，甲乙两位同学为了提高解方程能力，勤加练习，但甲同学在解一元一次方程 $\frac{x + 3}{2} - 1 = \frac{x + a}{6}$ ，去分母时-1项忘记乘以6，得该方程的解为 $x = - 3$ ，乙同学在解方程组 ${\begin{matrix} 2 x - 3 b y = 5 \\ 3 x + 2 b y = 3 \end{matrix}$ 时，看错了第一个方程，得该方程组的解为 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$ ，试求 $a + b$ 的值.

查看试题解析
21. 列方程组解应用题：
甲、乙两人相距6km，两人同时出发相向而行，1小时相遇；同时出发同向而行，甲3小时可追上乙．两人的平均速度各是多少？

查看试题解析
22. 《一千零一夜》中：有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食．树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞来一只，则树下的鸽子就是整个鸽群的 $\frac{1}{3}$ ；若从树上飞下去一只，则树上、树下的鸽子就一样多了．”你知道树上、树下各有多少只鸽子吗？

查看试题解析
23. 某工厂的一条流水线匀速生产出产品，在有一些产品积压的情况下，经过试验，若安排9人包装，则5小时可以包装完所有产品；若安排6人包装，则需要10小时才能包装完所有产品．假设每个人的包装速度一样，现要在2小时内完成产品包装的任务，问至少需要安排多少人？

查看试题解析
24. 小颖家准备装修一套房子，若请甲、乙两个装修公司合作，则需6周完成，需花费工钱5.2万元；若先请甲公司单独做4周后，剩下的请乙公司来做；则还需9周才能完成，需花费工钱4.8万元.若只请一个公司单独完成，从节约开支的角度来考虑，小颖家应该选甲公司还是乙公司？

查看试题解析