2021-2022学年浙教版七年级下册期中复习专题5二元一次方程综合（尖子生班）

试卷更新日期：2022-04-01 类型：复习试卷

进入出卷网下载

一、单选题

1. 由2x+3y﹣6＝0可以得到用x表示y的式子为（　　）

A、 $y = - \frac{2}{3} x - 2$ B、 $y = \frac{2}{3} x - 2$ C、 $y = \frac{2}{3} x + 2$ D、 $y = - \frac{2}{3} x + 2$

查看试题解析
2. 现有一批脐橙运往外地销售，A型车载满一次可运3吨，B型车载满一次可运4吨，现有脐橙31吨，计划同时租用A，B两种车型，一次运完且恰好每辆车都载满脐橙，租车方案共有（　　）

A、2种 B、3种 C、4种 D、5种

查看试题解析
3. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知加密规则为：明文a，b，c对应密文a+1，-a+2b+4，b+3c+9，如果接收方收到密文7，12，22，则解密得到的明文为（）

A、6，2，7 B、2，6，7 C、6，7，2 D、7，2，6

查看试题解析
4. 已知关于x，y的方程组 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解为 ${\begin{matrix} x = 2 \\ y = 4 \end{matrix}$ ，则关于方程组 ${\begin{matrix} a_{1} (x + 1) + 2 b_{1} (y - 1) = 3 c_{1} \\ a_{2} (x + 1) + 2 b_{2} (y - 1) = 3 c_{2} \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = 5 \\ y = 7 \end{matrix}$ B、 ${\begin{matrix} x = 5 \\ y = 13 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 3 \end{matrix}$ D、 ${\begin{matrix} x = 1 \\ y = 7 \end{matrix}$

查看试题解析
5. 自行车的轮胎安装在前轮上行驶3000千米后报废，安装在后轮上，只能行驶2000千米，为了行驶尽可能多的路程，采取在自行车行驶一定路程后，用前后轮调换使用的方法，那么安装在自行车上的这对轮胎最多可行驶多少千米？（）

A、2300千米 B、2400千米 C、2500千米 D、2600千米

查看试题解析
6. 利用两块完全一样的长方体木块测量一张桌子的高度，首先按图①所示的方式放置，再交换两木块的位置，按图②所示的方式放置．量的数据如图，则桌子的高度等于（）

A、 $80 cm$ B、 $75 cm$ C、 $70 cm$ D、 $65 cm$

查看试题解析
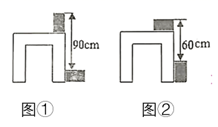7. 我们规定： $[m]$ 表示不超过 $m$ 的最大整数，例如： $[3.1] = 3$ ， $[0] = 0$ ， $[- 3.1] = - 4$ ，则关于 $x$ 和 $y$ 的二元一次方程组 ${\begin{array}{l} [x] + y = 3.2 \\ x - [y] = [3.2] \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 0.2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1.2 \end{array}$ C、 ${\begin{array}{l} x = 3.3 \\ y = 0.2 \end{array}$ D、 ${\begin{array}{l} x = 3.4 \\ y = 0.2 \end{array}$

查看试题解析
8. 如图，分别用火柴棍连续搭建正三角形和正六边形，公共边只用一根火柴棍，如果搭建的正三角形和正六边形共用了2023根火柴，并且正三角形的个数比正六边形的个数多 $6$ 个，那么能连续搭建的正三角形的个数是（）

A、 $229$ B、 $281$ C、 $287$ D、 $293$

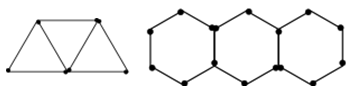查看试题解析
9. 我国古代数学家张丘建在《张丘建算经）里，提出了“百钱买百鸡”这个有名的数学问题.用100个钱买100只鸡，公鸡每只五个钱，母鸡每只三个钱，小鸡每个钱三只.问公鸡，小鸡各买了多少只？在这个问题中，小鸡的只数不可能是（）

A、87 B、84 C、81 D、78

查看试题解析
10. 若二元一次方程3x﹣y=7，2x+3y=1，y=kx﹣9有公共解，则k的取值为（）

A、3 B、﹣3 C、﹣4 D、4

查看试题解析
11. 已知一个四位数的十位数字加1等于它的个位数字，个位数字加1等于它的百位数字，把这个四位数倒序排列所成的数与原数的和等于10769，则该四位数的数字之和为（　　）。

A、25 B、24 C、33 D、34

查看试题解析
12. 一列快车和一列慢车的长分别为180米和225米，若同向行驶，从快车追及慢车起到全部超过，需81秒．现设快车的车速为x米/秒，慢车的车速为y米/秒，则表示其等量关系的式子是（　　）

A、 $81 (x - y) = 225$ B、 $81 (x - y) = 180$ C、 $81 (x - y) = 225 - 180$ D、 $81 (x - y) = 225 + 180$

查看试题解析

二、填空题

13. 若关于x，y的二元一次方程ax+by=2有一个解是 ${\begin{cases} x = 1 \\ y = - 1 \end{cases}$ ，则代数式2a-2b+3的值是.

查看试题解析
14. 若方程组 ${\begin{cases} x - (c + 3) x y = 3 \\ x^{a - 2} - y^{b + 3} = 4 \end{cases}$ 是关于x，y的二元次方程组，则代数式a+b+c=.

查看试题解析
15. 若x，y是方程组 ${\begin{cases} 123 x + 200 y = 8 ① \\ 321 x + 244 y = 880 ② \end{cases}$ 的解，则x+y的值为.

查看试题解析
16. 若关于x，y的方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} ， \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解为 ${\begin{array}{l} x = 5 ， \\ y = 6 ， \end{array}$ 则方程组 ${\begin{array}{l} 3 a_{1} x + 2 b_{1} y = a_{1} + c_{1} ， \\ 3 a_{2} x + 2 b_{2} y = a_{2} + c_{2} \end{array}$ 的解为.

查看试题解析
17. 山脚下有一池塘，泉水以固定的流量（即单位时间里流入池中的水量相同）不停地向池塘内流淌．现池塘中有一定深度的水，若用一台A型抽水机抽水，则1小时正好能把池塘中的水抽完；若用两台A型抽水机抽水，则20分钟正好把池塘中的水抽完．问若用三台A型抽水机同时抽，则需要分钟恰好把池塘中的水抽完．

查看试题解析
18. 若x＋y＋z＝15，－3x－y＋z＝－25，x、y、z皆为非负数，记整式5x+4y+z的最大值为a，最小值为b，则a﹣b =.

查看试题解析

三、计算题

19. 判断下列二元一次方程有无整数解，并说明理由．

(1)、2x+6y=5；

(2)、4x+6y=8；

(3)、3x+5=6y+11；

(4)、 $x = \frac{11 - 2 y}{3}$ ．

查看试题解析
20. ${\begin{matrix} \begin{matrix} 3 x + 2 y + 2 z = 5 \\ 2 x + 3 y + 2 z = 7 \end{matrix} \\ 2 x + 2 y + 3 z = 9 \end{matrix}$

查看试题解析

四、解答题

21. 4月9日上午8时，2017 徐州国际马拉松赛鸣枪开跑，一名岁的男子带着他的两个孩子一同参加了比赛，下面是两个孩子与记者的对话：

根据对话内容，请你用方程的知识帮记者求出哥哥和妹妹的年龄.

查看试题解析
22. 用浓度分别为25％和20％的两种溶液，配成浓度为22％的溶液100克．问两种溶液各需取多少克?

查看试题解析
23. 试将100分成两个正整数之和，其中一个为11的倍数，另一个为17的倍数．

查看试题解析
24. 一个三位数，个位，百位上的数字的和等于十位上的数字，百位上的数字的7倍比个位，十位上的数字的和大2，个位，十位，百位上的数字的和是14，求这个三位数.

查看试题解析
25. 若干名游客要乘坐游船，要求每艘游船乘坐的人数相同．如果每艘游船乘坐12人，结果剩下1人未能上船；若有一艘游船空着开走，则所有游客正好能平均分坐到其余游船上．已知每艘游船最多能容纳15人．请你通过计算，说明游客共有多少人？

查看试题解析
26. 制造某种产品，1人用机器，3人靠手工，每天可制造60件；2人用机器，2人靠手工，每天可制造80件.3人用机器，1人靠手工，每天可制造多少件产品?

查看试题解析