浙江省温州市2022年初中学业水平适应性考试数学试卷（一）

试卷更新日期：2022-04-01 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分，每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 数2，-1，0， $- \frac{2}{3}$ 中最小的是（）

A、2 B、-1 C、0 D、 $- \frac{2}{3}$

查看试题解析
2. 下列选项中的垃圾分类图标，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 银河系大约有恒星160 000 000 000颗，数据160 000 000 000用科学记数法表示为（）

A、0.16×10¹² B、1.6×10¹¹ C、16×10¹⁰ D、160×10⁹

查看试题解析
4. 在一个不透明的布袋里装有3个白球，2个黑球，它们除颜色外其余都相同．现随机从布袋中摸出1个球，是白球的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
5. 计算（-x²） ·（-x³）⁴的结果为（）

A、-x⁹ B、x⁹ C、-x¹⁴ D、x¹⁴

查看试题解析
6. 如图，在4×7的方格中，点A，B， C， D在格点上，线段CD是由线段AB位似放大得到，则它们的位似中心是（）

A、点P₁ B、点P₂ C、点P₃ D、点P₄

查看试题解析
7. 如图，圆形挂钟分针针尖到圆心的距离为10cm，经过35分钟，分针针尖转过的弧长是（）

A、 $\frac{25}{6}$ πcm B、 $\frac{25}{3}$ πcm C、 $\frac{35}{6}$ πcm D、 $\frac{35}{3}$ πcm

查看试题解析
8. 如图，小慧的眼睛离地面的距离为 $1.6 m$ ，她用三角尺测量广场上的旗杆高度，仰角恰与三角板 $60 °$ 角的边重合，量得小慧与旗杆之间的距离 $B C$ 为 $5 m$ ，则旗杆 $A D$ 的高度（单位：m）为（）

A、6.6 B、11.6 C、 $1.6 + \frac{5 \sqrt{3}}{3}$ D、 $1.6 + 5 \sqrt{3}$

查看试题解析
9. 在平面直角坐标系中，二次函数y= $- \frac{1}{2}$ x² +bx+6（b≤1）的图象交x轴于点A，B （点A在B的左侧）．当-1≤x≤3时，函数的最大值为8，则b的值为（）

A、-1 B、 $- \frac{3}{2}$ C、-2 D、 $- \frac{5}{2}$

查看试题解析
10. 如图，在Rt△ABC中，∠ACB 90°，以其三边为边向外作正方形．P是AE边上一点，连结PC并延长交HI于点Q，连结CG交AB于点K．若 $\frac{P C}{C Q} = \frac{3}{4}$ ，则 $\frac{C K}{K G}$ 的值为（）

A、 $\frac{12}{25}$ B、 $\frac{3}{4}$ C、 $\frac{13}{25}$ D、 $\frac{4}{5}$

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

11. 因式分解：m²- 6m+9 =

查看试题解析
12. 不等式 $\frac{1 - 2 x}{4}$ ≤3的解为

查看试题解析
13. 如图，在Rt△ABC中，∠A=90°，⊙O是它的内切圆，分别切AB，BC，CA于点D， E，F．若∠ACB=40°，则∠DOE=度．

查看试题解析
14. 对某班同学课外活动最喜欢的项目进行问卷调查（每人选一项），绘制成如图所示的统计图．已知选踢毽子的人数比选打篮球的人数少9入，则选“其他”项目的有人。

查看试题解析
15. 如图，矩形OABC的边OA，OC分别在×轴、y轴上，点B在反比例函数y= $\frac{k}{x}$ （k>0，×>0）的图象上，且AB= $\sqrt{3}$ ．将矩形OABC沿×轴正方向平移 $\frac{3}{2}$ 个单位得矩形OA'B'C，A'B'交反比例函数图象于点D，且∠DAA'=30°，则k的值为

查看试题解析
16. 如图1是某小车侧面示意图，图2是该车后备箱开起侧面示意图，具体数据如图所示（单位： cm），且AC=BD，AF∥BE，sin∠BAF=0.8，箱盖开起过程中，点A，C，F不随箱盖转动，点B，D，E绕点A沿逆时针方向转动相同角度，分别到点B'，D'，E’的位置，气簧活塞杆CD随之伸长为CD'．当直线BE⊥B'E'，CD'≈2CD 时，AB的长为cm，CD'的长为cm

查看试题解析

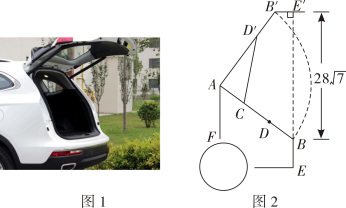
三、解答题（本题有8小题，共80分。解答需写出必要的文字说明、演算步骤或证明过程）

17.

(1)、计算： $\sqrt{16}$ +（π-2）⁰+（-4）．

(2)、化简：（x+3）² -x（x-1）．

查看试题解析
18. 如图，在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F．

(1)、求证：BE=DF．

(2)、当∠BAD=110°时，求∠EAF的度数．

查看试题解析

19. 某中学分年级段开展主题为“垃圾分类知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级，划分等级后的2个年级段的数据整理如下：

九年级“垃坡分类知多少"调查的统计表

等级	非常了解	比较了解	基本了解	不了解
频数	40	120	36	4
频率	0.20	0.60	0.18	0.02

(1)、本次问卷调查选取的九年级的样本容量为

(2)、若给四个等级分别赋分如下表：

等级	非常了解	比较了解	基本了解	不了解
分值（分）	5	3	1	0

请结合你所学过的统计知识，选出你认为知识掌握较好的一个年级段，并说明理由．

查看试题解析

20. 如图，在7×13的方格纸中，A，B是方格纸中的两格点，请按要求作图．

(1)、在图1中，以AB为一边作一个矩形ABCD，要求C，D两点也在格点上。

(2)、在图2中，以AB为一边作一个菱形ABEF，要求E，F两点也在格点上。

查看试题解析
21. 如图，在平面直角坐标系中，二次函数y=x²+bx+3的图象交×轴于点A，B（点A在点B的左侧），交y轴于点C，CD∥x轴交抛物线于点D，CD=4．

(1)、求这个二次函数的表达式．

(2)、已知点E在抛物线上且位于x轴下方，过E作y轴的平行线交CD于点F．当EF=2DF时，求点E的坐标．

查看试题解析
22. 如图，在△ABC中，AB=AC，以AB为直径作⊙O分别交AC，BC于点D，E，连结EO并延长交00于点F，连结AF．

(1)、求证：四边形ACEF是平行四边形．

(2)、连结DE，若△CDE的面积为20，cos∠F= $\frac{\sqrt{5}}{5}$ ，求⊙O的直径．

查看试题解析
23. 某电商准备销售甲，乙两种特色商品．已知每件甲商品的进价比每件乙商品的进价多20元，用5000元购进甲型商品的数量与用4500元购进乙商品的数量相等．甲，乙两种商品的销售单价分别为在其进价基础上增加60%和50%．

(1)、求甲、乙两种商品每件进价分别为多少元？

(2)、该电商平均每天卖出甲商品200件，乙商品100件．经调查发现，甲，乙两种商品销售单价都降低1元，这两种商品每天都可多销售2件，为了使每天获取更大的利润，该电商决定把甲，乙两种商品的销售单价都下降m元．在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲，乙两种商品获取的总利润最大？

查看试题解析
24. 如图1，在平面直角坐标系中，A为（4，4），B为（1，0），AC⊥y轴于点C、D是线段OC上一点，作AE⊥AD交×轴于点E，取DE的中点F，连结BF．设OD的长为a．

(1)、求证：AD=AE．

(2)、当a=3时，求tan∠FBE的值．

(3)、当∠CAD等于△BEF中的一个内角时，求a的值．

查看试题解析