河南省郑州市2021年中考数学模拟试卷(三)
试卷更新日期:2022-04-01 类型:中考模拟
一、单选题
-
1. 若a的相反数是2,则a的值为( )A、2 B、﹣2 C、﹣ D、±22. 2020年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30日成功定点于距离地球36002公里的地球同步轨道.将36000用科学记数法表示应为( )A、 B、 C、 D、3. 如图所示,左边立体图形的俯视图为( ).
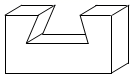 A、
A、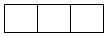 B、
B、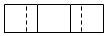 C、
C、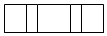 D、
D、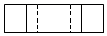 4. 下列各式中正确的是( )A、 B、 C、 D、5. 学校为了培养学生的践行精神和吃苦品质,每学期以班级为单位申报校内志愿者活动.2020年秋季学期某班40名学生参与志愿者活动情况如下表,则他们参与次数的众数和中位数分别是( )
4. 下列各式中正确的是( )A、 B、 C、 D、5. 学校为了培养学生的践行精神和吃苦品质,每学期以班级为单位申报校内志愿者活动.2020年秋季学期某班40名学生参与志愿者活动情况如下表,则他们参与次数的众数和中位数分别是( )参与次数
1
2
3
4
5
人数
6
17
14
2
1
A、2,2 B、17,2 C、17,1 D、2,36. 《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的 ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )A、 B、 C、 D、7. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根8. 某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为( )A、 B、 C、 D、9. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点 处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( ) A、 B、 C、 D、10. 对称轴为直线x=1的抛物线 (a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数), ⑥当x<-1时,y随x的增大而增大,其中结论正确的个数为( )
A、 B、 C、 D、10. 对称轴为直线x=1的抛物线 (a、b、c为常数,且a≠0)如图所示,小明同学得出了以下结论:①abc<0,②b2>4ac,③4a+2b+c>0,④3a+c>0,⑤a+b≤m(am+b)(m为任意实数), ⑥当x<-1时,y随x的增大而增大,其中结论正确的个数为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
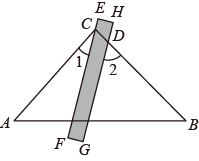
11. 计算(2-3)2的结果等于12. 如图,将三角板与两边平行的直尺()贴在一起,使三角板的直角顶点C()在直尺的一边上,若 , 则的度数等于.
 13. 不等式组1< x﹣2≤2的所有整数解的和为.14. 如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为.
13. 不等式组1< x﹣2≤2的所有整数解的和为.14. 如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧,交AC于点E,若∠A=60°,∠ABC=100°,BC=4,则扇形BDE的面积为.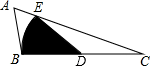 15. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.
15. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.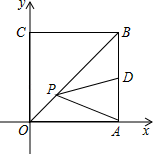
三、解答题
-
16. 先化简再求值: ÷(a﹣ ),其中a=2cos30°+1,b=tan45°.17. 某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
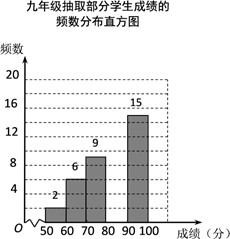

成绩x/分
频数
频率
第1段
x<60
2
0.04
第2段
60≤x<70
6
0.12
第3段
70≤x<80
9
b
第4段
80≤x<90
a
0.36
第5段
90≤x≤100
15
0.30
请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、样本中,部分学生成绩的中位数落在第段;(4)、已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?18. 如图,在平面直角坐标系中,一次函数y=mx+5(m≠0)的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.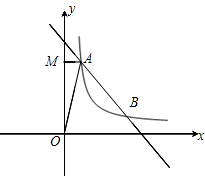 (1)、求一次函数和反比例函数的表达式.(2)、求△OAM的面积S.(3)、在y轴上求一点P,使PA+PB的值最小,并求出此时点P的坐标.19. 如图, 是 的直径, 是半圆上任意一点,连接 并延长到点 ,使得 ,连接 ,点 是弧 的中点.
(1)、求一次函数和反比例函数的表达式.(2)、求△OAM的面积S.(3)、在y轴上求一点P,使PA+PB的值最小,并求出此时点P的坐标.19. 如图, 是 的直径, 是半圆上任意一点,连接 并延长到点 ,使得 ,连接 ,点 是弧 的中点.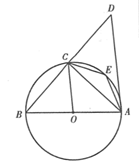 (1)、证明: .(2)、①当 时, 是直角三角形;
(1)、证明: .(2)、①当 时, 是直角三角形;②当 时,四边形 是菱形.
20. 如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm , 连杆BC=CD=20cm , BC , CD与AB始终在同一平面内.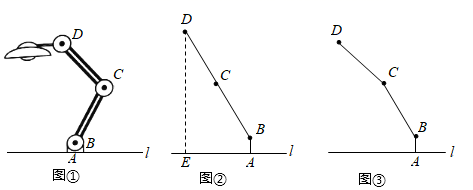
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
(1)、如图②,转动连杆BC , CD , 使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE .(2)、将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了cm .21. 某公司开发出一款新的节能产品,该产品的成本价为8元/件,该产品在正式投放市场前通过代销点进行了为期一个月30天的试销售,售价为13元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成如图所示的图象,图中的折线表示日销量(件)与销售时间(天)之间的函数关系.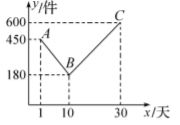 (1)、直接写出与之间的函数解析式,并写出的取值范围.(2)、若该节能产品的日销售利润为(元),求与之间的函数解析式.日销售利润不超过1950元的共有多少天?(3)、若 , 求第几天的日销售利润最大,最大的日销售利润是多少元?22. 如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°.
(1)、直接写出与之间的函数解析式,并写出的取值范围.(2)、若该节能产品的日销售利润为(元),求与之间的函数解析式.日销售利润不超过1950元的共有多少天?(3)、若 , 求第几天的日销售利润最大,最大的日销售利润是多少元?22. 如图,两个等腰直角△ABC和△CDE中,∠ACB=∠DCE=90°. (1)、观察猜想如图1,点E在BC上,线段AE与BD的数量关系是_ , 位置关系是_.(2)、探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;(3)、拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在同一条直线上时,请直接写出AD的长.23. 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,﹣3),对称轴是直线x=1.
(1)、观察猜想如图1,点E在BC上,线段AE与BD的数量关系是_ , 位置关系是_.(2)、探究证明把△CDE绕直角顶点C旋转到图2的位置,(1)中的结论还成立吗?说明理由;(3)、拓展延伸:把△CDE绕点C在平面内自由旋转,若AC=BC=13,DE=10,当A、E、D三点在同一条直线上时,请直接写出AD的长.23. 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,﹣3),对称轴是直线x=1. (1)、求二次函数的解析式;(2)、若M是第四象限抛物线上一动点,且横坐标为m,设四边形OCMA的面积为s.请写出s与m之间的函数关系式,并求出当m为何值时,四边形OCMA的面积最大;(3)、设点B是x轴上的点,P是抛物线上的点,是否存在点P,使得以A,B、C,P四点为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、若M是第四象限抛物线上一动点,且横坐标为m,设四边形OCMA的面积为s.请写出s与m之间的函数关系式,并求出当m为何值时,四边形OCMA的面积最大;(3)、设点B是x轴上的点,P是抛物线上的点,是否存在点P,使得以A,B、C,P四点为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.