河南省信阳市息县2021年中招适应性考试二数学试卷（A卷）

试卷更新日期：2022-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 在-2，-1，0，1这四个数中，最小的数是（）

A、-2 B、-1 C、0 D、1

查看试题解析
2. 2020年7月23日，中国首颗火星探测器“天问一号”顺利升空，当“天问一号”探测器抵达火星附近时，总飞行里程将达到470000000公里.470000000这个数字用科学记数法表示为（）

A、 $4.7 \times 10^{7}$ B、 $4.7 \times 10^{8}$ C、 $4.7 \times 10^{9}$ D、 $47 \times 10^{7}$

查看试题解析
3. 一把直尺和一块三角板 $A B C$ (含 $30 °$ 、 $60 °$ 角)如图所示摆放，直尺一边与三角板的两直角边分别交于点 $D$ 和点 $E$ ，另一边与三角板的两直角边分别交于点 $F$ 和点 $A$ ，且 $∠ C E D = 50 °$ ，那么 $∠ B F A$ 的大小为（）

A、 $145 °$ B、 $140 °$ C、 $135 °$ D、 $130 °$

查看试题解析
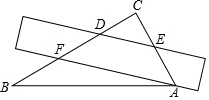4. 如图是由10个同样大小的小正方体摆成的几何体．将小正方体①移走后，则关于新几何体的三视图描述正确的是（）

A、俯视图不变，左视图不变 B、主视图改变，左视图改变 C、俯视图不变，主视图不变 D、主视图改变，俯视图改变

查看试题解析
5. 若a为正整数，则 $\frac{(a \cdot a ⋯ ⋯ a)^{2}}{a 个}$ ＝（）

A、a^2a B、2aa C、aa D、 $a^{2}$

查看试题解析
6. 某同学要统计本校图书馆最受学生欢迎的图书种类，以下是排乱的统计步骤：
①从扇形图中分析出最受学生欢迎的种类

②去图书馆收集学生借阅图书的记录

③绘制扇形图来表示各个种类所占的百分比

④整理借阅图书记录并绘制频数分布表

正确统计步骤的顺序是（　　）

A、②→③→①→④ B、③→④→①→② C、①→②→④→③ D、②→④→③→①

查看试题解析
7. 已知关于x的一元二次方程 $x^{2} + b x - 2 = 0$ ，则下列关于该方程根的判断，正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关

查看试题解析
8. 如图，在平面直角坐标系中，一次函数 $y = \frac{4}{3} x + 4$ 的图象与x轴、y轴分别相交于点B、点A，以线段AB为边作正方形ABCD，且点C在反比例函数 $y = \frac{k}{x} (x < 0)$ 图象上，则k的值为（）

A、21 B、－42 C、42 D、－21

查看试题解析
9. 如果一个数等于两个连续奇数的平方差，那么我们称这个数为“幸福数”.下列数中为“幸福数”的是（）

A、205 B、250 C、502 D、520

查看试题解析
10. 在平面直角坐标系中，矩形ABCD的边BC在 $x$ 轴上，顶点 $A (- 4 ， 6) ， C (4 ， 0)$ ，连接AC按照下列方法作图：（1）以点C为圆心，适当的长度为半径画弧分别交CA，CD于点E，F；（2）分别以点E，F为圆心，大于 $\frac{1}{2} E F$ 的长为半径画弧交于点G；（3）作射线CG交AD于H，则点H的横坐标为（）

A、6 B、4 C、3 D、1

查看试题解析

二、填空题

11. 计算 $\sqrt{18} \div \sqrt{2}$ 的结果是.

查看试题解析
12. 《易经》是中国传统文化的精髓.如图是易经的一种卦图，图中每一卦由三根线组成（线形为或），如正北方向的卦为 .从图中三根线组成的卦中任取一卦，这一卦中恰有2根和1根的概率为.

查看试题解析
13. 不等式组 ${\begin{cases} \frac{3 - x}{2} \leq 0 \\ 3 x + 2 \geq 1 \end{cases}$ 的解集是。

查看试题解析
14. 如图，矩形ABCD中，AB＝6，BC＝8，点P是矩形ABCD内一动点，且S_△PAB＝S_△PCD，则PC＋PD的最小值为.

查看试题解析
15. 如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝6，点D是AC上一动点，连接BD，将△ABD沿BD折叠，点A落在A′处，当点A′在△ABC内部（不含边界）时，AD长的取值范围.

查看试题解析

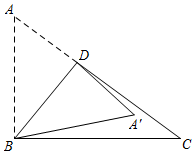
三、解答题

16. 先化简，再求值： $(\frac{x}{x - 1} - 1) \div \frac{x^{2} + 2 x + 1}{x^{2} - 1}$ ，其中 $x = \sqrt{2} - 1$ .

查看试题解析

17. 为落实视力保护工作，某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力，活动后再次测查这部分学生的视力.两次相关数据记录如下：

活动前被测查学生视力数据：
（1）4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6
（2）4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据：
（2）4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8
（3）4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动后被测查学生视力频数分布表

分组	频数
$4.0 ⩽ x < 4.2$	1
$4.2 ⩽ x < 4.4$	2
$4.4 ⩽ x < 4.6$	b
$4.6 ⩽ x < 4.8$	7
$4.8 ⩽ x < 5.0$	12
$5.0 ⩽ x < 5.2$	4

根据以上信息回答下列问题：

(1)、填空：

a =

，

b =

，活动前被测查学生视力样本数据的中位数是，活动后被测查学生视力样本数据的众数是；

(2)、若视力在4.8及以上为达标，估计七年级600名学生活动后视力达标的人数有多少？

(3)、分析活动前后相关数据，从一个方面评价学校开展视力保健活动的效果.

查看试题解析

18. 小红帮弟弟荡秋千(如图1)，秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示．

(1)、根据函数的定义，请判断变量h是否为关于t的函数?

(2)、结合图象回答：
①当t=0.7s时，h的值是多少?并说明它的实际意义．

②秋千摆动第一个来回需多少时间?

查看试题解析
19. 图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时，钢条可放入底盒中（底盒固定在地面下），此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图，经测量，钢条AB＝AC＝50cm，∠ABC＝47°.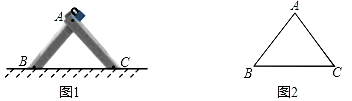

(1)、求车位锁的底盒长BC.

(2)、若一辆汽车的底盘高度为30cm，当车位锁上锁时，问这辆汽车能否进入该车位?（参考数据：sin47°≈0.73，cos47°≈0.68，tan47°≈1.07）

查看试题解析

20. 请阅读材料，并完成相应的任务.

在数学探究课上，同学们在探索与圆有关的角的过程中发现这些角的两边都与圆相交，不断改变顶点的位置，可形成无数个角，而根据点和圆的位置关系可将这些角分为三类，分别是顶点在圆上、圆外和圆内的角结合教学课上学习的圆周角的概念，对顶点在圆外和圆内的角进行定义：顶点在圆外，两边与圆相交的角叫做圆外角.顶点在圆内，两边都与圆相交的角叫做圆内角，如图1， $∠ A P_{1} B$ 和 $∠ A P_{2} B$ 分别是 $\overset{⌢}{A B}$ 所对的圆外角和圆内角.

如图2，点 $A ， B$ 在 $⊙ O$ 上， $∠ A P B$ 为 $\overset{⌢}{A B}$ 所对的一个圆外角. $A P ， B P$ 分别交 $⊙ O$ 于点 $C ， D$ .若 $∠ A O B = 120 ° ， \overset{⌢}{C D}$ 所对的圆心角为 $50 °$ ，求 $∠ A P B$ .勤奋小组的解题过程（部分）如下：

解：如图2，连接 $A D ， O C ， O D$ .

$∵ ∠ A D B$ 是 $\overset{⌢}{A B}$ 所对的圆周角，且 $∠ A O B = 120 °$ ，

$∴ ∠ A D B = \frac{1}{2} ∠ A O B = 60 °$ .

…

任务：

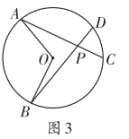(1)、如图1，在探究与圆有关的角时，运用的数学思想方法是：____；

A、公理化思想 B、分类讨论 C、数形结合

(2)、将勤奋小组的解题过程补充完整；

(3)、如图3，当点

P

在

⊙ O

内时，

∠ A P B

是

\overset{⌢}{A B}

所对的一个圆内角，延长

A P

交

⊙ O

于点

C

，延长

B P

交

⊙ O

于点

D

，若设

∠ A O B = m ° ， \overset{⌢}{C D}

所对的圆心角为

n °

，则

∠ A P B =

°.

查看试题解析

21. 如图，抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，且OB＝OC＝3OA.

(1)、求抛物线的解析式及对称轴.

(2)、在抛物线上任取一点M，过点M作MN//x轴，且四边形ABMN为平行四边形，在线段MN上任取一点P，过点P作x轴的垂线交抛物线于点Q，记点Q的纵坐标为yQ.当点M到抛物线对称轴的距离不超过1个单位长度时，求yQ的取值范围.

查看试题解析

22. 如图，Q是弧AB与直径AB所围成的图形的内部的一定点，P是直径AB上一动点，连接PQ并延长交弧AB于点C.连接AC.已知AB＝6cm，设A，P两点间的距离为xcm，P，C两点间的距离为y₁cm，A、C两点间的距离为y₂cm.

小腾根据学习函数的经验，分别对函数y₁ ， y₂随自变量x的变化而变化的规律进行了探究.下面是小腾的探究过程，请补充完整：

(1)、技照如表中自变量x的值进行取点、画图、测量，分别得到了y₁ ， y₂与x的几组对应值；

x/cm	0	1	2	3	4	5	6
y₁/cm	5.62	4.67	3.76		2.65	3.18	4.37
y₂/cm		5.59	5.53	5.42	5.19	4.73	4.11

(2)、在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y₁），并画出函数y₁的图象；

(3)、结合函数图象，解决问题：当△APC为等腰三角形时，AP的长度约为cm.（保留2位小数）

查看试题解析

23. 问题背景：在课外小组活动中，“创新小组”对“正方形旋转”问题进行了探究，如图①，边长为6的正方形ABCD的对角线相交于点E，分别延长EA到点F，EB到点H，使AF＝BH，再以EF，EH为邻边做正方形EFGH，连接AH，DF；

(1)、解决问题：AH与DF之间的数量关系是，位置关系是；

(2)、深入研究：如图②正方形EFGH固定不动，将正方形ABCD绕点E顺时针方向旋转α°，判断AH与DF的关系，并证明：

(3)、拓展延伸：如图③，在正方形ABCD旋转过程中（0 °＜α＜90 °），AB，BC分别交EF，EH于点M，N，连接MN，EC.
①当AM＝2时，直接写出S_△BMN＋S_△CEN的值；
②若α＝45°，在不添加字母的情况下，请你在图中再找两个点，和点M，N所围成的四边形是特殊四边形，直接写出这个特殊四边形.（写两个，不需要证明，需要指明是什么特殊四边形）

查看试题解析