河南省信阳市固始县2021年九年级第一次适应性考试数学试卷
试卷更新日期:2022-04-01 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 2020年中央财政下达义务教育补助经费1695.9亿元,比上年增长8.3%.其中1695.9亿元用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元3. 下列采用的调查方式中,不合适的是( )A、了解澧水河的水质,采用抽样调查. B、了解一批灯泡的使用寿命,采用全面调查. C、了解张家界市中学生睡眠时间,采用抽样调查. D、了解某班同学的数学成绩,采用全面调查.4. 下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是( )A、
 B、
B、 C、
C、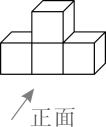 D、
D、 5. 将含30°角的一个直角三角板和一把直尺如图放置,若 ,则 等于( )
5. 将含30°角的一个直角三角板和一把直尺如图放置,若 ,则 等于( )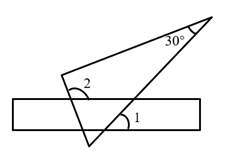 A、80° B、100° C、110° D、120°6. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )
A、80° B、100° C、110° D、120°6. 如图,函数 与函数 的图象相交于点 .若 ,则x的取值范围是( )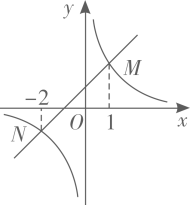 A、 或 B、 或 C、 或 D、 或7. 定义新运算 ,对于任意实数a,b满足 ,其中等式右边是通常的加法、减法、乘法运算,例如 ,若 (k为实数) 是关于x的方程,则它的根的情况是( )A、有一个实根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根8. 目前以 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 用户2万户,计划到2021年底全市 用户数累计达到8.72万户.设全市 用户数年平均增长率为 ,则 值为( )A、 B、 C、 D、9. 如图,已知Rt△AOB的顶点O(0,0),∠AOB=90°,点B在x轴正半轴上,点A在y轴正半轴上,按以下步骤作图:①以点A为圆心,适当长为半径作弧,分别交AO,AB于点M,N;②分别以点M、N为圆心,大于的长为半径作弧,两弧交于点P,连接AP,交BO于点C.过点C作CD⊥BO交AB于点D.若CD=2,∠B=30°,则点A的坐标为( )
A、 或 B、 或 C、 或 D、 或7. 定义新运算 ,对于任意实数a,b满足 ,其中等式右边是通常的加法、减法、乘法运算,例如 ,若 (k为实数) 是关于x的方程,则它的根的情况是( )A、有一个实根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根8. 目前以 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 用户2万户,计划到2021年底全市 用户数累计达到8.72万户.设全市 用户数年平均增长率为 ,则 值为( )A、 B、 C、 D、9. 如图,已知Rt△AOB的顶点O(0,0),∠AOB=90°,点B在x轴正半轴上,点A在y轴正半轴上,按以下步骤作图:①以点A为圆心,适当长为半径作弧,分别交AO,AB于点M,N;②分别以点M、N为圆心,大于的长为半径作弧,两弧交于点P,连接AP,交BO于点C.过点C作CD⊥BO交AB于点D.若CD=2,∠B=30°,则点A的坐标为( ) A、(0,3) B、(0,4) C、(0,5) D、(0,6)10. 如图①,在矩形ABCD中,点M从点A出发以每秒1个单位长度的速度匀速运动到点B,点N沿A-D-C-B的顺序匀速运动,速度为每秒2个单位长度,当点M运动到点B时,M、N同时停止运动,设点M出发t秒时,△AMN的面积为S,如果S与t的函数关系如图②所示(其中0≤t≤2和6≤t≤8段为抛物线,2≤t≤6段为线段),那么下列说法不正确的是( )
A、(0,3) B、(0,4) C、(0,5) D、(0,6)10. 如图①,在矩形ABCD中,点M从点A出发以每秒1个单位长度的速度匀速运动到点B,点N沿A-D-C-B的顺序匀速运动,速度为每秒2个单位长度,当点M运动到点B时,M、N同时停止运动,设点M出发t秒时,△AMN的面积为S,如果S与t的函数关系如图②所示(其中0≤t≤2和6≤t≤8段为抛物线,2≤t≤6段为线段),那么下列说法不正确的是( )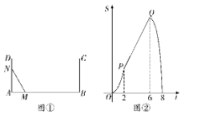 A、当点M运动到点B时,点N也运动到点B B、矩形ABCD的周长是12 C、当2≤t≤6时,S=2t D、当t=7时,S=7
A、当点M运动到点B时,点N也运动到点B B、矩形ABCD的周长是12 C、当2≤t≤6时,S=2t D、当t=7时,S=7二、填空题
-
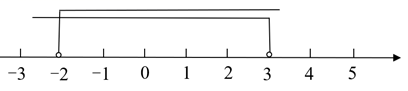
11. 写出一个负数,使这个数的绝对值小于3.12. 关于 的不等式组 的解集在数轴上如图表示,则 的值为.
 13. 如图,在矩形ABCD中,AB=6,AD=8,E、F分别为AB、CD边上的点,且EF∥BC,G为EF上一点,且GF=2,M、N分别为GD、EC的中点,则MN=.
13. 如图,在矩形ABCD中,AB=6,AD=8,E、F分别为AB、CD边上的点,且EF∥BC,G为EF上一点,且GF=2,M、N分别为GD、EC的中点,则MN=.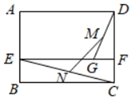 14. 如图,在扇形AOB中,OA=4,∠AOB=90°,点P是弧AB上的动点,连接OP,点C是线段OP的中点,连接BC并延长交OA于点D,则图中阴影部分面积最小值为.
14. 如图,在扇形AOB中,OA=4,∠AOB=90°,点P是弧AB上的动点,连接OP,点C是线段OP的中点,连接BC并延长交OA于点D,则图中阴影部分面积最小值为.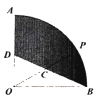
三、解答题
-
15. 现有四张分别标有数字-1,-1,0,2的卡片,它们除数字外完全相同.把卡片背面朝上洗匀,从中随机抽取一张,记下数字不放回,再随机抽取一张,则两次抽出的卡片上的数字相同的概率是.16. 先化简,再求值:( ﹣1)÷ ,其中a= +2.17. “黄河宁,天下平.”这是2019年9月份习主席在郑州主持召开黄河流域生态保护和高质量发展座谈会上的讲话内容.为积极响应政府号召,甲、乙两校举办了以“生态文明与环境保护”为主题的作文竞赛,为了了解甲、乙两校学生“生态文明与环境保护”作文竞赛成绩的情况,从甲、乙两校各随机抽取20名学生的竞赛成绩(百分制,成绩取整数),进行了整理和分析,过程如下:
收集数据
甲校 68 88 100 100 79 94 89 85 100 88 100 90 98 97 77 94 96 100 92 67
乙校 69 97 91 69 98 100 99 100 90 100 97 89 97 100 99 94 79 99 98 79
整理数据
学校成绩段
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲校
2
a
b
12
乙校
2
2
1
15
分析数据
学校统计量
平均数
中位数
众数
甲校
90.1
93
d
乙校
92.2
c
100
根据以上信息,回答下列问题:
(1)、表中a=_ , b=_ , c=_ , d=_;(2)、若甲校共有400名同学参加此次竞赛,估计甲校成绩超过86分的学生人数;(3)、在此次竞赛中,你认为哪个学校学生的“生态文明与环境保护”作文竞赛的成绩较好?请说明理由.18. 如图,已知⊙O的直径AB=4,点C、D分别为⊙O上的两点, , 过点D作DE⊥AB于点E,⊙O的切线DF与直线AF交于点F,且AF过点C,连接BD、AD.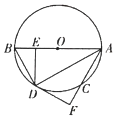 (1)、求证:CF=BE;(2)、填空:
(1)、求证:CF=BE;(2)、填空:①当AD=时,四边形AODC是菱形;
②当AD=时,四边形AEDF是正方形.
19. 清明上河园是以画家张择端的写实画作《清明上河图》为蓝本,按照《营造法式》为建设标准,再现了古都汴京千年繁华的盛景.如图①,园内的拂云阁雄健端庄又不失隽秀舒展,是园内登高远眺绝佳处.某数学兴趣小组为了测量拂云阁的高度,小组成员小亮站在点D处测得拂云阁顶的仰角是37°,沿直线向前走23米到达点C处,测得拂云阁顶的仰角是60°,已知小亮的眼睛到地面的距离DE=1.5米,拂云阁底端B和测量点C、D在同一条直线上,示意图如图②所示,求拂云阁的高度.(结果保留整数,参考数据: , sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)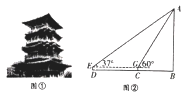 20. 某新建成学校举行美化绿化校园活动,九年级计划购买A,B两种花木共100棵绿化操场,其中A花木每棵50元,B花木每棵100元.(1)、若购进A,B两种花木刚好用去8000元,则购买了A,B两种花木各多少棵?(2)、如果购买B花木的数量不少于A花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用.21. 在平面直角坐标系xOy中,直线y=-2x+2分别与x,y轴交于A,B两点,点C(0,m)在线段OB上,抛物线y=ax2+bx+c(a≠0)经过A,C两点,且与x轴交于另一点D.(1)、求点D的坐标(用只含a,m的代数式表示);(2)、当时,若点P(n,y1),Q(4,y2)均在抛物线y=ax2+bx+c上,且y1>y2 , 求实数n的取值范围;22. 如图,点E在弦AB所对的优弧上,且弧BE为半圆,C是弧BE上的动点,连接CA,CB.已知AB=4cm,设B,C两点间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A,C两点间的距离为y2cm.
20. 某新建成学校举行美化绿化校园活动,九年级计划购买A,B两种花木共100棵绿化操场,其中A花木每棵50元,B花木每棵100元.(1)、若购进A,B两种花木刚好用去8000元,则购买了A,B两种花木各多少棵?(2)、如果购买B花木的数量不少于A花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用.21. 在平面直角坐标系xOy中,直线y=-2x+2分别与x,y轴交于A,B两点,点C(0,m)在线段OB上,抛物线y=ax2+bx+c(a≠0)经过A,C两点,且与x轴交于另一点D.(1)、求点D的坐标(用只含a,m的代数式表示);(2)、当时,若点P(n,y1),Q(4,y2)均在抛物线y=ax2+bx+c上,且y1>y2 , 求实数n的取值范围;22. 如图,点E在弦AB所对的优弧上,且弧BE为半圆,C是弧BE上的动点,连接CA,CB.已知AB=4cm,设B,C两点间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A,C两点间的距离为y2cm.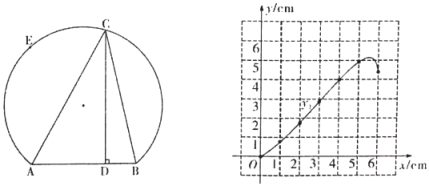
小明根据学习函数的经验,分别对函数y1 , y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)、按照表中自变量x的值进行取点、画图、测量,分别得到了y1 , y2与x的几组对应值;x/cm
0
1
2
3
4
5
6
y1/cm
0
0.78
1.76
2.85
3.98
4.95
4.47
y2/cm
4
4.69
5.26
a
5.96
5.94
4.47
上表中a的值为_.
(2)、在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x.y2),并画出函数y1的图象如图所示.请在同一坐标系中画出函数y2的图象;(3)、结合函数图象,解决问题:①连接BE,则BE的长约为_cm;
②当以A,B,C为顶点组成的三角形是直角三角形时,BC的长度约为_cm.
23. 如图,在△ABC中,∠BAC=120°,AB=AC= , 将△ABC绕点A逆时针旋转a得到△ADE,连接BD,EC,BD的延长线交EC的延长线于点F. (1)、【问题发现】如图①,当α=60°时,线段BF与EF的数量关系是 , ∠BFE=;(2)、【类比探究】当△ABC旋转到如图②所示的位置时,请判断线段BF与EF的数量关系及∠BFE的度数,并说明理由;(3)、【问题解决】当AE∥BC时,请直接写出线段BF的长.
(1)、【问题发现】如图①,当α=60°时,线段BF与EF的数量关系是 , ∠BFE=;(2)、【类比探究】当△ABC旋转到如图②所示的位置时,请判断线段BF与EF的数量关系及∠BFE的度数,并说明理由;(3)、【问题解决】当AE∥BC时,请直接写出线段BF的长.