河南省焦作市武陟县2021年中考数学一检试卷

试卷更新日期：2022-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 若a的相反数为 $\frac{5}{2}$ ，则a的值为（）

A、﹣ $\frac{2}{5}$ B、﹣ $\frac{5}{2}$ C、 $\frac{5}{2}$ D、 $\frac{2}{5}$

查看试题解析
2. 2020年，某市从强化政策支持、做强电商园区、培育地头企业、发展直播电商、开展电商扶贫等方面发力，累计实现网络交易额1805.2亿元，数据“1805.2亿”用科学记数法表示为（）

A、 0.18052×10¹² B、1.8052×10¹¹ C、1.8052×10¹² D、0.18052×10¹¹

查看试题解析
3. 如图，AB∥CD，GH⊥EF于G，∠1＝28°，则∠2的度数为（）

A、28° B、152° C、62° D、118°

查看试题解析
4. 如图是由大小相同的正方体搭成的几何体，将小正方体①去掉后，下列说法正确的是（）

A、主视图不变 B、俯视图不变 C、左视图不变 D、三种视图都不变

查看试题解析
5. 计算﹣m²n•（﹣ $\frac{1}{2}$ mn³）的结果是（）

A、 $\frac{1}{2}$ m⁴n³ B、 $\frac{1}{2}$ m³n³ C、﹣ $\frac{1}{2}$ m³n⁴ D、 $\frac{1}{2}$ m³n⁴

查看试题解析
6. 某超市销售A，B，C，D四种品牌的冷饮，某天的销售情况如图所示，则该超市应多进的冷饮品牌是（）

A、A品牌 B、B品牌 C、C品牌 D、D品牌

查看试题解析
7. 已知关于x的一元二次方程x²+bx+c＝0，其中b，c在数轴上的对应点如图所示，则这个方程的根的情况是（）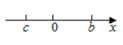

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根

查看试题解析
8. 已知点A（﹣1，6），B（m，y₁），C（m+1，y₂）在反比例函数y＝ $\frac{k}{x}$ 的图象上，若m＞0，则y₁ ， y₂的大小关系是（）

A、y₁＞y₂＞6 B、y₁＜y₂＜6 C、y₁＝y₂＝6 D、无法确定

查看试题解析
9. 如图，在▱ABCD中，以点B为圆心，适当长度为半径作弧，分别交AB，BC于点F，G，再分别以点F，G为圆心，大于 $\frac{1}{2}$ FG长为半径作弧，两弧交于点H，作射线BH交AD于点E，连接CE，若AE＝10，DE＝6，CE＝8，则BE的长为（）

A、4 $\sqrt{5}$ B、8 $\sqrt{5}$ C、2 $\sqrt{41}$ D、40 $\sqrt{2}$

查看试题解析
10. 如图，在平面直角坐标系中，四边形OABC是菱形，∠AOC＝120°，点B的坐标为（6，0），点D是边BC的中点，现将菱形OABC绕点O顺时针旋转，每秒旋转60°，则第2021秒时，点D的坐标为（）

A、（ $\frac{9}{2}$ ， $\frac{3}{2} \sqrt{3}$ ） B、（﹣ $\frac{9}{2}$ ，﹣ $\frac{3}{2} \sqrt{3}$ ） C、（ $\frac{9}{2}$ ，﹣ $\frac{3}{2} \sqrt{3}$ ） D、（﹣ $\frac{9}{2}$ ， $\frac{3}{2} \sqrt{3}$ ）

查看试题解析

二、填空题

11. 请写出一个大于 $- \sqrt{5}$ 且小于 $\sqrt{2}$ 的整数：.

查看试题解析
12. 不等式组 ${\begin{matrix} - x > \frac{1}{2} \\ x + 3 \leq 2 \end{matrix}$ 的解集是.

查看试题解析
13. 一个不透明的袋子中装有仅颜色不同的4个红球和1个黄球，从袋子中随机摸出两个球，则摸出的两个球的颜色相同的概率是.

查看试题解析
14. 如图，某图书阅览室摆放桌椅如下：按此规律摆放，2n+1（n是不小于4的自然数）人需要张桌子.

查看试题解析
15. 如图，在扇形BOC中，∠BOC＝60°，点D是 $\overset{⌢}{B C}$ 的中点，点E，F分别为半径OC，OB上的动点.若OB＝2，则△DEF周长的最小值为.

查看试题解析

三、解答题

16. 先化简，再求值： $(1 - \frac{a + 2}{a - 2}) \div \frac{a^{2} - 2 a}{a^{2} - 4 a + 4}$ ，其中 $a = \sqrt{3}$ .

查看试题解析

17. 为了了解同学们每月零花钱的数额，校园小记者随机调查了本校50名同学，并将调查的结果进行收集，整理，绘制成如图（表）的频数分布表和频数分布直方图：

a.零花钱数额的频数分布表

零花钱数额（元）	0≤x＜30	30≤x＜60	60≤x＜90	90≤x＜120	120≤x＜150
频数	4	m	20	n	2

b.零花钱数额的频数分布直方图

c.零花钱数额在90≤x＜120这一组的为：90， 90， 91 ，93 ，95， 100 ，100 ，105

根据以上信息，回答下列问题：

(1)、表中m的值为， n 的值为；

(2)、请补全频数分布直方图；

(3)、该校共有学生2800人，若零花钱数额超过100元（含100）的视为“零花钱较多”，请估计该校学生中“零花钱较多”的人数.

查看试题解析

18. 如图，AB为半圆O的直径，点C为半圆上不与A，B重合的一动点， $\overset{⌢}{A C}$ ＝ $\overset{⌢}{C D}$ ，连接AC，CD，AD，BC，延长BC交AD于F，交半圆O的切线AE于E.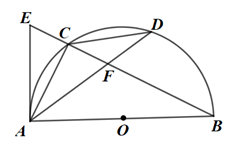

(1)、求证：△AEF是等腰三角形；

(2)、填空：
①若AE＝ $\sqrt{5}$ ，BE＝5，则BF的长为；

②当∠E的度数为时，四边形OACD为菱形.

查看试题解析

19. 某“综合实践”小组在学习了“利用三角函数测高”这节后，开展了测量底部可以到达的物体的高度的实践活动，并撰写如下活动报告（不完整）：

数学活动报告

活动小组：清北组

活动地点：学校操场

活动时间：2020年12月22日

活动记录：小航

活动课题	测量旗杆的高度
活动工具	测倾器和皮尺
测量示意图			说明：线段MN表示旗杆，测点A到旗杆底部N的水平距离AN可以直接测得，点C在MN上.
测量数据	测量项目	第一次	第二次	平均值
	仰角∠MBC	21°	23°	a
	水平距离AN	25.4m	25.6m	b
	侧倾器的高度AB	1.5m	1.5m	c
计算过程
测量结果
……

(1)、填空：a＝， b＝， c＝；

(2)、活动报告中设置“平均值”栏的主要目的是；

(3)、根据以上信息，请补全报告中的计算过程和测量结果.（精确到0.1m.参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40）

查看试题解析

20. 某商店销售A、B两种品牌的书包，已知购买1个A品牌书包和2个B品牌书包共需550元；购买2个A品牌书包和1个B品牌书包共需500元.

(1)、求这两种品牌书包的单价；

(2)、某商店对这两种品牌的书包给出优惠活动：A种品牌的书包按原价的八折销售，B种品牌的书包10个以上超出部分按原价的五折销售.
①设购买x个A品牌书包的费用为y₁元，购买x个B品牌书包的费用为y₂元，请分别求出y₁ ， y₂与x的函数关系式；

②学校准备购买同一种品牌的书包，如何选择购买更省钱？

查看试题解析
21. 如图，抛物线 $y = x^{2} + 2 x - c$ 与x轴负半轴，y轴负半轴分别交于点A，C，且 $O A = O C$ ，它的对称轴为直线l.

(1)、求抛物线的表达式及顶点坐标.

(2)、P是直线 $A C$ 上方对称轴上的一动点，过点P作 $P Q ⊥ A C$ 于点Q.若 $P Q = P O$ ，求点P的坐标.

查看试题解析
22. 小航在学习中遇到这样一个问题：
如图，点C是 $\overset{⌢}{A B}$ 上一动点，直径AB＝8cm，过点C作CD $∥$ AB交 $\overset{⌢}{A B}$ 于D，O为AB的中点.连接OC，OD，当△ABC的面积为3.5cm²时，求线段CD的长.
小航结合学习函数的经验研究此问题，请将下面的探究过程补充完整：

(1)、根据点C在 $\overset{⌢}{A B}$ 上的不同位置，画出相应的图形，测量线段CD，OC的长度和△OCD的面积，得到下表的几组对应值（当点C与点A或点B重合时，△OCD的面积为0）.
CD/cm
0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
$S_{Δ O C D}$ $/ c m^{2}$
0
1.9
3.9
5.6
m
7.8
7.9
6.8
0
填空：m＝（结果保留一位小数）；

(2)、将线段CD的长度作为自变量x，△OCD的面积是x的函数，记为y，请在平面直角坐标系xOy中画出函数的图象，并写出△OCD面积的最大值；

(3)、在同一坐标系中画出所需的图象，并结合图象直接写出：当△OCD的面积为3.5cm²时，线段CD长度的近似值（结果保留一位小数）.

查看试题解析
23. 如图

(1)、问题发现
如图1，△ABC与△ADE都是等腰直角三角形，且∠BAC＝∠DAE＝90°，直线BD，CE交于点F，直线BD，AC交于点G.则线段BD和CE的数量关系是，位置关系是；

(2)、类比探究
如图2，在△ABC和△ADE中，∠ABC＝∠ADE＝α，∠ACB＝∠AED＝β，直线BD，CE交于点F，AC与BD相交于点G.若AB＝kAC，试判断线段BD和CE的数量关系以及直线BD和CE相交所成的较小角的度数，并说明理由；

(3)、拓展延伸
如图3，在平面直角坐标系中，点M的坐标为（3.0），点N为y轴上一动点，连接MN.将线段MN绕点M逆时针旋转90得到线段MP，连接NP，OP.请直接写出线段OP长度的最小值及此时点N的坐标.

查看试题解析

CD/cm	0	1.0	2.0	3.0	4.0	5.0	6.0	7.0	8.0
$S_{Δ O C D}$ $/ c m^{2}$	0	1.9	3.9	5.6	m	7.8	7.9	6.8	0