2022年中考数学二轮专题复习-二次函数的图像和性质
试卷更新日期:2022-04-01 类型:二轮复习
一、单选题
-
1. 二次函数y=(x-3)2+1的最小值是( )A、3 B、-3 C、1 D、-12. 将二次函数 的图象向左平移1个单位长度, 再向上平移2个单位后, 所得图象 的函数解析式是( )A、 B、 C、 D、3. 抛物线 的对称轴是直线( )A、 B、 C、 D、4. 抛物线的顶点坐标为( )A、 B、 C、 D、5. 根据以下表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,可以判断方程ax2+bx+c=0的一个解x的范围是( )
x
0
0.5
1
1.5
2
y=ax2+bx+c
-1
-0.5
1
3.5
7
A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<26. 二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:x
…
0
1
2
3
4
…
y
…
4
5
4
﹣4
﹣20
﹣45
…
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A、﹣45 B、﹣20 C、﹣4 D、07. 已知二次函数 (其中m>0),下列说法正确的是( )A、当x>2时,都有y随着x的增大而增大 B、当x<3时,都有y随着x的增大而减小 C、若x<n时,都有y随着x的增大而减小,则 D、若x<n时,都有y随着x的增大而减小,则8. 若A(﹣6,y1),B(﹣3,y2),C(1,y3)为二次函数y=2x2﹣1图象上的三点,则y3 , y2 , y1的大小关系是( )A、y3<y2<y1 B、y2<y3<y1 C、y3<y1<y2 D、y2<y1<y39. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b>0,③4a﹣2b+c>0,④3a+c>0,其中正确的结论个数为( )
 A、1个 B、2个 C、3个 D、4个10. 如图,已知点A( ,2), B(0,1),射线AB绕点A逆时针旋转30°,与x轴交于点C,则过A,B,C三点的二次函数y=ax2+bx+1中a,b的值分别为( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知点A( ,2), B(0,1),射线AB绕点A逆时针旋转30°,与x轴交于点C,则过A,B,C三点的二次函数y=ax2+bx+1中a,b的值分别为( ) A、 B、 C、 D、11. 已知二次函数 是常数, 的图象经过点 和 ,且当 时,函数 的最小值为 ,最大值为1,则 的取值范围是( )A、 B、 C、 D、12. 如图,正方形OABC的边长为2,OC与y轴正半轴的夹角为30°,点A在抛物线 的图象上,则a的值为( )
A、 B、 C、 D、11. 已知二次函数 是常数, 的图象经过点 和 ,且当 时,函数 的最小值为 ,最大值为1,则 的取值范围是( )A、 B、 C、 D、12. 如图,正方形OABC的边长为2,OC与y轴正半轴的夹角为30°,点A在抛物线 的图象上,则a的值为( )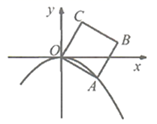 A、 B、 C、 D、13. 已知函数 的对称轴为直线 .若 是方程 的两个根,且 ,则下列说法正确的是( )
A、 B、 C、 D、13. 已知函数 的对称轴为直线 .若 是方程 的两个根,且 ,则下列说法正确的是( ) A、 B、 C、 D、14. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、15. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①:②;③;④ . 正确的有( )
A、 B、 C、 D、14. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、15. 如图,已知二次函数的图象与x轴交于点 , 与y轴的交点B在和之间(不包括这两点),对称轴为直线 . 下列结论:①:②;③;④ . 正确的有( ) A、1个 B、2个 C、3个 D、4个16. 如图,将函数y(x+4)2+5的图象沿y轴向下平移得到一条新函数的图象,其中点A(﹣6,m),B(﹣1,n)平移后的对应点分别为点A'、B',若曲线AB扫过的面积为30(图中的阴影部分),则新图象的函数表达式是( )
A、1个 B、2个 C、3个 D、4个16. 如图,将函数y(x+4)2+5的图象沿y轴向下平移得到一条新函数的图象,其中点A(﹣6,m),B(﹣1,n)平移后的对应点分别为点A'、B',若曲线AB扫过的面积为30(图中的阴影部分),则新图象的函数表达式是( ) A、y(x+4)2﹣2 B、y(x+4)2﹣1 C、y(x+4)2+2 D、y(x+4)2+117. 二次函数y=x2的图象如图所示,点A0 位于坐标原点,A1 , A2 , A3 , …,A2023在y轴的正半轴上,B1 , B2 , B3 , …,B2023在二次函数y=x2第一象限的图象上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2022B2023A2023都是等边三角形,则△A2022B2023A2023的周长是( )
A、y(x+4)2﹣2 B、y(x+4)2﹣1 C、y(x+4)2+2 D、y(x+4)2+117. 二次函数y=x2的图象如图所示,点A0 位于坐标原点,A1 , A2 , A3 , …,A2023在y轴的正半轴上,B1 , B2 , B3 , …,B2023在二次函数y=x2第一象限的图象上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2022B2023A2023都是等边三角形,则△A2022B2023A2023的周长是( )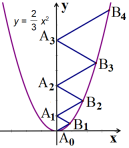 A、6069 B、6066 C、6063 D、606018. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、6069 B、6066 C、6063 D、606018. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )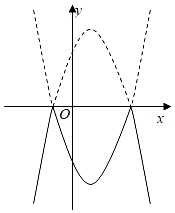 A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣319. 如图,抛物线 (a>0)与x轴交于A,B,顶点为点D,把抛物线在x轴下方部分关于点B作中心对称,顶点对应D′,点A对应点C,连接DD′,CD′,DC,当△CDD′是直角三角形时,a的值为( )
A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣319. 如图,抛物线 (a>0)与x轴交于A,B,顶点为点D,把抛物线在x轴下方部分关于点B作中心对称,顶点对应D′,点A对应点C,连接DD′,CD′,DC,当△CDD′是直角三角形时,a的值为( ) A、 或 B、 或 C、 或 D、 或20. 对于每个非零自然数n,抛物线 与x轴交于 , 两点,以 表示这两点之间的距离,则 的值是( )A、 B、 C、 D、1
A、 或 B、 或 C、 或 D、 或20. 对于每个非零自然数n,抛物线 与x轴交于 , 两点,以 表示这两点之间的距离,则 的值是( )A、 B、 C、 D、1二、填空题
-
21. 在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表.
x
-3
-2
-1
1
2
3
4
5
y
-14
-7
-2
2
m
n
-7
-14
则m-n的值为 .
22. 已知抛物线与轴的一个交点为 , 则 .23. 如图,已知 的半径为1,圆心P在抛物线 上运动,当 与x轴相切时,圆心P的横坐标为. 24. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为.25. 如果抛物线(其中a、b、c是常数,且a≠0)在对称轴左侧的部分是下降的,那么a0.(填“<”或“>”)26. 点A(x1 , y1),B(x2 , y2)(x1·x2≥0)是y=ax2(a≠0)图象上的点,存在=1时,=1成立,写出一个满足条件a的值27. 抛物线为常数)的顶点为 , 且抛物线经过点 , 下列结论:① , ② , ③ , ④时,存在点使为直角三角形.其中正确结论的序号为.28. 如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为 .
24. 点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为.25. 如果抛物线(其中a、b、c是常数,且a≠0)在对称轴左侧的部分是下降的,那么a0.(填“<”或“>”)26. 点A(x1 , y1),B(x2 , y2)(x1·x2≥0)是y=ax2(a≠0)图象上的点,存在=1时,=1成立,写出一个满足条件a的值27. 抛物线为常数)的顶点为 , 且抛物线经过点 , 下列结论:① , ② , ③ , ④时,存在点使为直角三角形.其中正确结论的序号为.28. 如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为 . 29. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,抛物线 的顶点 在线段 上,与 轴相交于 , 两点,设点 , 的横坐标分别为 , ,且 .若 是-1,则 的最大值是.
29. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,抛物线 的顶点 在线段 上,与 轴相交于 , 两点,设点 , 的横坐标分别为 , ,且 .若 是-1,则 的最大值是. 30. 已知抛物线 ( 为常数, )经过点 ,点 是x轴正半轴上的动点.点 在抛物线上,当 的最小值为 时,b的值为.
30. 已知抛物线 ( 为常数, )经过点 ,点 是x轴正半轴上的动点.点 在抛物线上,当 的最小值为 时,b的值为.三、计算题
-
31.(1)、解方程:2x2+1=3x;(2)、将二次函数 配方成y=a(x﹣h)2+k的形式.32. 已知抛物线y=﹣2x2+(m﹣3)x﹣8.(1)、若抛物线的对称轴为y轴,求m的值;(2)、若抛物线的顶点在x正半轴上,求m的值.33. 用适当的方法解下列方程:(1)、2x2﹣8x=0.(2)、x2﹣3x+4=0.(3)、y= x2﹣x+3,求出抛物线的开口方向、对称轴、顶点坐标.34.
如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.

(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.35. 如图,矩形ABCD中,AD=3,AB=4,点P是对角线AC上一动点(不与A,C重合),连结BP,作PE⊥PB,交射线DC于点E,以线段PE,PB为邻边作矩形BPEF.过点P作GH⊥CD,分别交AB、CD于点G、H.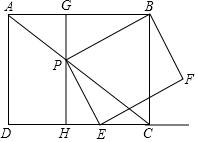 (1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.
(1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.四、解答题
-
36. 已知二次函数的图象经过 , 两点,求b,c的值.37. 已知二次函数 的图象如图所示,求 的面积.
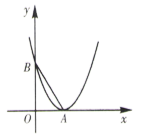 38. 一个半圆和抛物线的一部分围成的“芒果”如图所示,已知点A , B , C , D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线对应的解析式为y= x2﹣ ,求CD的长.
38. 一个半圆和抛物线的一部分围成的“芒果”如图所示,已知点A , B , C , D分别是“芒果”与坐标轴的交点,AB是半圆的直径,抛物线对应的解析式为y= x2﹣ ,求CD的长.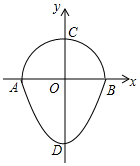 39. 如图,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.
39. 如图,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.(Ⅰ)求抛物线的解析式;
(Ⅱ)若抛物线交y轴于点C,在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由;
(Ⅲ)在抛物线第二象限的图象上是否存在一点P,使得△PBC的面积最大?若存在,请直接写出点P的坐标和△PBC面积的最大值;若不存在,请说明理由.
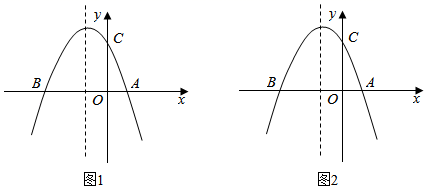 40. 如图,是某座抛物线型的隧道示意图,已知路面AB宽24米,抛物线最高点C到路面AB的距离为8米,为保护来往车辆的安全,在该抛物线上距路面AB高为6米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(提示:以AB所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系)
40. 如图,是某座抛物线型的隧道示意图,已知路面AB宽24米,抛物线最高点C到路面AB的距离为8米,为保护来往车辆的安全,在该抛物线上距路面AB高为6米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(提示:以AB所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系) 41. 抛物线 过点 和点 ,与 轴交于点 ,顶点为点D.
41. 抛物线 过点 和点 ,与 轴交于点 ,顶点为点D.(Ⅰ)求点 的坐标;
(Ⅱ)点 是线段 上一动点,过点 作直线 轴,交抛物线于点 ,连接 并延长交 轴于点 ,连接 .若 的面积是 面积的2倍,求点 的坐标;
(Ⅲ)抛物线上一点 ,点 的横坐标是 ,连接 ,与 轴交于点 ,点 是线段 上一动点(不与点 ,点 重合)将 沿 所在直线翻折,得到 ,当 与 重叠部分的面积是 面积的 时,求线段 的长度.
42. 如图,在平面直角坐标系中, 为原点,抛物线 ( , 为常数),经过点 和点 .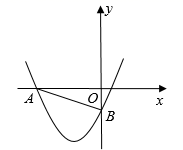 (1)、求抛物线的解析式;(2)、在抛物线上是否存在一点 ,使 ?若存在,请求出点 的坐标,若不存在,请说明理由;(3)、点 为直线 下方抛物线上一点,点 为 轴上一点,当 的面积最大时,直接写出 的最小值.43. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
(1)、求抛物线的解析式;(2)、在抛物线上是否存在一点 ,使 ?若存在,请求出点 的坐标,若不存在,请说明理由;(3)、点 为直线 下方抛物线上一点,点 为 轴上一点,当 的面积最大时,直接写出 的最小值.43. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
44. 如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ,x1•x2= ) (1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(3)、在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.五、综合题
-
45. 如图,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(-2,0),直线BC的解析式为y= x-4.
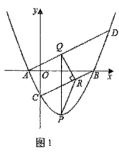
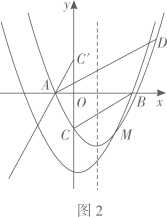 (1)、求抛物线的解析式;(2)、如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;(3)、如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.46. 如图,已知二次函数 的图象与x轴交于点A,B(点A在点B的左边),与y轴交于点C. 点P,Q为抛物线上两动点.
(1)、求抛物线的解析式;(2)、如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P的坐标;(3)、如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2 个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.46. 如图,已知二次函数 的图象与x轴交于点A,B(点A在点B的左边),与y轴交于点C. 点P,Q为抛物线上两动点. (1)、若点P坐标为(1,3),求抛物线的表达式;(2)、如图①连结BC,在(1)的条件下,是否存在点Q,使得∠BCQ=∠ABC. 若存在,请求出点Q的坐标,若不存在,请说明理由;(3)、若点P为抛物线顶点,连结OP,当 a 的值从-3变化到-1的过程中,求线段OP扫过的面积.
(1)、若点P坐标为(1,3),求抛物线的表达式;(2)、如图①连结BC,在(1)的条件下,是否存在点Q,使得∠BCQ=∠ABC. 若存在,请求出点Q的坐标,若不存在,请说明理由;(3)、若点P为抛物线顶点,连结OP,当 a 的值从-3变化到-1的过程中,求线段OP扫过的面积.