浙教版备考2022年中考数学二轮复习训练题13:动态几何问题
试卷更新日期:2022-04-01 类型:二轮复习
一、单选题
-
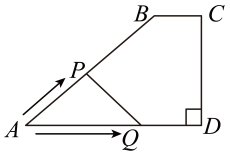
1. 在四边形ABCD中,∠A=45°,∠D=90°,AD∥BC,BC=1,CD=3.点P,Q同时从点A出发,点P以个单位长度/秒向点B运动,到达点B停止运动;点Q以2个单位长度/秒沿着AD→DC向点C运动,到达点C停止运动.设点Q运动时间为ts,△APQ的面积为S,则S随t变化的函数图象大致为( )
 A、
A、 B、
B、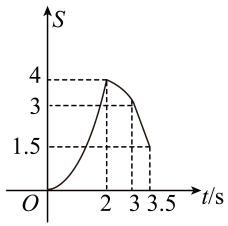 C、
C、 D、
D、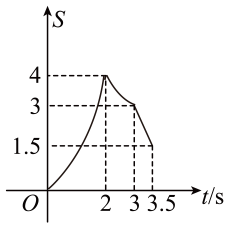 2. 如图,点M、N分别是正方形ABCD的边BC、CD上的两个动点,在运动过程中保持∠MAN=45°,连接EN、FM相交于点O,以下结论:①MN=BM+DN;②BE2+DF2=EF2;③BC2=BF•DE;④OM=OF( )
2. 如图,点M、N分别是正方形ABCD的边BC、CD上的两个动点,在运动过程中保持∠MAN=45°,连接EN、FM相交于点O,以下结论:①MN=BM+DN;②BE2+DF2=EF2;③BC2=BF•DE;④OM=OF( )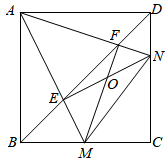 A、①②③ B、①②④ C、②③④ D、①②③④3. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )
A、①②③ B、①②④ C、②③④ D、①②③④3. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )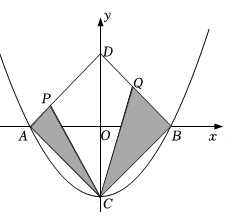 A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小4. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )
A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小4. 如图,正方形ABCD的边长为3,将长为2 的线段QF的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在AB上滑动,同时点F在BC上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段QF的中点M所经过的路线长为( )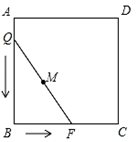 A、 B、 C、 D、5. 如图, 中, , , ,点 是 边上的一个动点,将线段 绕点 顺时针旋转 得到线段 ,连接 ,则在点 运动过程中,线段 的最小值为( )
A、 B、 C、 D、5. 如图, 中, , , ,点 是 边上的一个动点,将线段 绕点 顺时针旋转 得到线段 ,连接 ,则在点 运动过程中,线段 的最小值为( ) A、 B、 C、 D、6. 如图,直线 与x轴、y 轴分别相交于点A、B两点,圆心P的坐标为(2,0).⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是( )
A、 B、 C、 D、6. 如图,直线 与x轴、y 轴分别相交于点A、B两点,圆心P的坐标为(2,0).⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是( )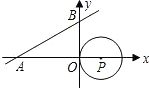 A、5 B、6 C、7 D、87. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM∶EN的值的变化情况是( )
A、5 B、6 C、7 D、87. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为斜边向外作等腰直角三角形△ACD,△BCE,弧AC和弧BC的中点分别是M,N.连接DM,EN,若C在半圆上由点A向B移动的过程中,DM∶EN的值的变化情况是( ) A、变大 B、变小 C、先变大再变小 D、保持不变8. 如图所示,在矩形纸片 中, ,点 分别是矩形的边 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 与 交于点 .则下列结论成立的是( )
A、变大 B、变小 C、先变大再变小 D、保持不变8. 如图所示,在矩形纸片 中, ,点 分别是矩形的边 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 与 交于点 .则下列结论成立的是( )① ;②当点 与点 重合时 ;③ 的面积 的取值范围是 ;④当 时, .
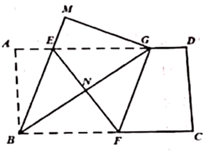 A、①③ B、③④ C、②③ D、②④9. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )
A、①③ B、③④ C、②③ D、②④9. 如图,将边长为 的正六边形 在直线l上由图 的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图 位置时,顶点 所经过的路径( )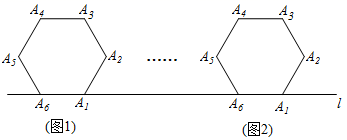 A、 B、 C、 D、10. 如图,正方形 的边长为a,点E在边 上运动(不与点A,B重合), ,点F在射线 上,且 与 相交于点G,连接 .则下列结论:① ,② 的周长为 ,③ ;④当 时,G是线段 的中点,其中正确的结论是( )
A、 B、 C、 D、10. 如图,正方形 的边长为a,点E在边 上运动(不与点A,B重合), ,点F在射线 上,且 与 相交于点G,连接 .则下列结论:① ,② 的周长为 ,③ ;④当 时,G是线段 的中点,其中正确的结论是( )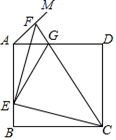 A、①②③ B、①④ C、①③④ D、①②③④
A、①②③ B、①④ C、①③④ D、①②③④二、填空题
-
11. 如图,已知Rt△ABC,∠C=90°,AC=BC=2,点M,N分别为CB,CA上的动点,且始终保持BM=CN,则AM+BN的最小值为 .
 12. 如图,△ABC中AB=AC,A (0,8),C (6,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的倍,要使整个运动时间最少,则点D的坐标应为 .
12. 如图,△ABC中AB=AC,A (0,8),C (6,0),D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的倍,要使整个运动时间最少,则点D的坐标应为 .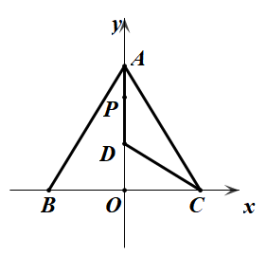 13. 如图所示,ABCD是边长为2的正方形,点E,F分别为边BC,CD上动点(点E不与B,C重合,点F不与C,D重合),且∠EAF=45°,下列说法:
13. 如图所示,ABCD是边长为2的正方形,点E,F分别为边BC,CD上动点(点E不与B,C重合,点F不与C,D重合),且∠EAF=45°,下列说法:①点E从B向C运动的过程中,△CEF的周长始终不变;
②以A为圆心,2为半径的圆一定与EF相切;
③△AEF面积有最小值;
④△CEF的面积最大值小于 .
其中正确的有 .(填写序号)
 14. 如图,在矩形ABCD中,AB=6,AD=8,点M,N分别为AD,AC上的动点(不含端点),AN=DM,连结点M与矩形的一个顶点,以该线段为直径作⊙O,当点N和矩形的另一个顶点也在⊙O上时,线段DM的长为 .
14. 如图,在矩形ABCD中,AB=6,AD=8,点M,N分别为AD,AC上的动点(不含端点),AN=DM,连结点M与矩形的一个顶点,以该线段为直径作⊙O,当点N和矩形的另一个顶点也在⊙O上时,线段DM的长为 . 15. 两块全等的等腰直角三角形如图放置,∠A=90°,DE交AB于点P,E在斜边BC上移动,斜边EF交AC于点Q,BP=3 ,BC=10,当△BPE是等腰三角形时,则AQ的长为 .
15. 两块全等的等腰直角三角形如图放置,∠A=90°,DE交AB于点P,E在斜边BC上移动,斜边EF交AC于点Q,BP=3 ,BC=10,当△BPE是等腰三角形时,则AQ的长为 . 16. 如图,⊙O的半径为2,圆心O到直线l的距离为4,有一内角为60°的菱形,当菱形的一边在直线l上,另有两边所在的直线恰好与⊙O相切,此时菱形的边长为 .
16. 如图,⊙O的半径为2,圆心O到直线l的距离为4,有一内角为60°的菱形,当菱形的一边在直线l上,另有两边所在的直线恰好与⊙O相切,此时菱形的边长为 .
三、综合题
-
17. 如图1,二次函数y=x2+bx-4的图象与x轴交于A(3,0)、B两点,与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AB,AC运动,其中一点到达端点时,另一点也随之停止运动.
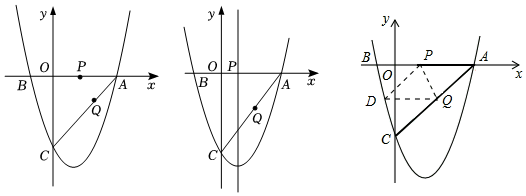 (1)、求该二次函数的解析式和点C的坐标;(2)、如图2,当点P、O同时运动秒时,停止运动,这时在抛物线对称轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出点E的坐标;若不存在,请说明理由;(3)、如图3,当P、Q运动t秒时,把△APQ沿PQ翻折,点A恰好落在抛物线上点D处,请判定此时四边形APDQ的形状,简要说明理由,并求出此时t的值.18. 在菱形ABCD中,对角线AC和BD相交于点O,且AC=16,BD=12.动点P从点A出发以2.5cm/s的速度沿折线A一B一C的路线向终点C运动.过点P作PQ⊥AC,垂足为Q,点Q关于点O的对称点为M,过点P,Q,M作⊙I.设运动时间为t秒.
(1)、求该二次函数的解析式和点C的坐标;(2)、如图2,当点P、O同时运动秒时,停止运动,这时在抛物线对称轴上是否存在点E,使得以A,E,Q为顶点的三角形为等腰三角形?若存在,请求出点E的坐标;若不存在,请说明理由;(3)、如图3,当P、Q运动t秒时,把△APQ沿PQ翻折,点A恰好落在抛物线上点D处,请判定此时四边形APDQ的形状,简要说明理由,并求出此时t的值.18. 在菱形ABCD中,对角线AC和BD相交于点O,且AC=16,BD=12.动点P从点A出发以2.5cm/s的速度沿折线A一B一C的路线向终点C运动.过点P作PQ⊥AC,垂足为Q,点Q关于点O的对称点为M,过点P,Q,M作⊙I.设运动时间为t秒.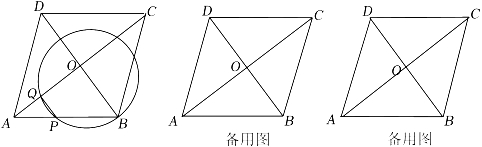 (1)、当t=1时,求AQ和PQ的长.
(1)、当t=1时,求AQ和PQ的长.
(2)、当P为AB中点时,请判断点B与⊙I的位置关系,并说明理由.(3)、在点P的整个运动过程中.①当t为何值时,⊙I经过点B.
②当t= ▲ 时,⊙I与边AB相切.
19. 在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC,连接OB,点D为OB的中点,点E是线段AB上的动点,连接DE,作DF⊥DE,交OA于点F,连接EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.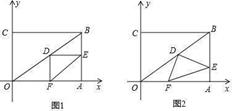 (1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中, 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出 的值.(3)、连接AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.20. 如图(1),在四边形ABCD中,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,设运动的时间为t(s),0<t<5
(1)、如图1,当t=3时,求DF的长.(2)、如图2,当点E在线段AB上移动的过程中, 的大小是否发生变化?如果变化,请说明理由;如果不变,请求出 的值.(3)、连接AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.20. 如图(1),在四边形ABCD中,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,设运动的时间为t(s),0<t<5 (1)、用含t的代数式表示AP;(2)、当以点A、P、Q为顶点的三角形与△ABD相似时,求t的值;(3)、如图(2),延长QP、BD,两延长线相交于点M,当△QMB为直角三角形时,求t的值.21. 已知,如图,在平面直角坐标系中,正方形ABCD,点A(0,10),点B(8,4),点C在第一象限,点P从顶点A出发,沿着正方形的边长逆时针运动一周,在OP右侧作∠OPQ=∠OAB交x轴于点Q.
(1)、用含t的代数式表示AP;(2)、当以点A、P、Q为顶点的三角形与△ABD相似时,求t的值;(3)、如图(2),延长QP、BD,两延长线相交于点M,当△QMB为直角三角形时,求t的值.21. 已知,如图,在平面直角坐标系中,正方形ABCD,点A(0,10),点B(8,4),点C在第一象限,点P从顶点A出发,沿着正方形的边长逆时针运动一周,在OP右侧作∠OPQ=∠OAB交x轴于点Q. (1)、求点C坐标.(2)、当点P与点B重合时,求OQ的长.(3)、在点P的整个运动过程中,当△OPQ是以PQ为腰的等腰三角形时,求OQ的长.22. 如图,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4).
(1)、求点C坐标.(2)、当点P与点B重合时,求OQ的长.(3)、在点P的整个运动过程中,当△OPQ是以PQ为腰的等腰三角形时,求OQ的长.22. 如图,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4). (1)、连接EF,若运动时间t=时,EF⊥AC;(2)、连接EP,当△EPC的面积为3cm2时,求t的值;(3)、若△EQP∽△ADC,求t的值.23. 如图, 在 中, , 点 以每秒2个单位长度的速度从点 出发, 沿 方向向终点 匀速运动, 同时点Q以每秒1个単位长度的速度从点 出发, 沿 方向向终点 匀速运动, 连结 . 设运动的时间为 秒.
(1)、连接EF,若运动时间t=时,EF⊥AC;(2)、连接EP,当△EPC的面积为3cm2时,求t的值;(3)、若△EQP∽△ADC,求t的值.23. 如图, 在 中, , 点 以每秒2个单位长度的速度从点 出发, 沿 方向向终点 匀速运动, 同时点Q以每秒1个単位长度的速度从点 出发, 沿 方向向终点 匀速运动, 连结 . 设运动的时间为 秒. (1)、求 的长 (用含 的代数式表示).(2)、当 秒时, 求 的面积.(3)、①如图 2,连结 ,当 为直角三角形时,求所有满足条件 的值.
(1)、求 的长 (用含 的代数式表示).(2)、当 秒时, 求 的面积.(3)、①如图 2,连结 ,当 为直角三角形时,求所有满足条件 的值.② 如图3,当点 关于 的对称点 落在直线 上时,求 的值.
24. 已知P是 上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP.若 . (1)、如图1,当 , , 时,求 ⊙O 的半径;(2)、在(1)的条件下,求四边形APBQ的面积(3)、如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若 ,探究直线AB与ON的位置关系,并说明理由.
(1)、如图1,当 , , 时,求 ⊙O 的半径;(2)、在(1)的条件下,求四边形APBQ的面积(3)、如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若 ,探究直线AB与ON的位置关系,并说明理由.