2021-2022学年浙教版七年级下册期中复习专题3 平行线的判定及性质（普通版）
试卷更新日期：2022-03-31 类型：复习试卷
一、单选题
-
1. 如图所示，若AB∥CD．则（ ）
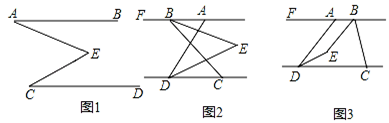
A、∠B=∠1 B、∠A=∠2 C、∠B=∠2 D、∠1=∠22. 如图，给出下列条件：① ；② ；③ ，且 ；④ 且 ；其中能推出 的条件为（ ）
A、①② B、②④ C、②③ D、②③④3. 如图，AB DE，BC⊥CD，则以下说法中正确的是（ ）
A、α，β的角度数之和为定值 B、α随β增大而增大 C、α，β的角度数之积为定值 D、α随β增大而减小4. 如图，已知GF⊥AB ， ∠1＝∠2，∠B＝∠AGH ， 则下列结论：①GH∥BC；②∠D＝∠F；③HE平分∠AHG；④HE⊥AB ， 其中正确的有（ ）
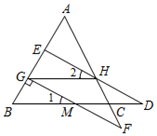A、1个 B、2个 C、3个 D、4个5. 将长方形ABCD纸片沿AE折叠，得到如图所示的图形，已知∠CED'=80°，则∠EAB的大小是（ ）
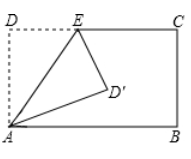A、60° B、50° C、75° D、55°6. 如图，将一直角三角板与两边平行的纸条如图所示放置，下列结论：
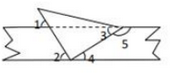
（1）∠1＝∠2；（2）∠3＝∠4；（3）∠2+∠4＝90°；（4）∠4+∠5＝180°，其中正确的个数是（ ）
A、1 B、2 C、3 D、47. 如图，在墙面上安装某一管道需经两次拐弯，拐弯后的管道与拐弯前的管道平行。若第一个弯道处∠B=142°，则第二个弯道处∠C的度数为（ ）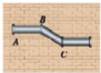
A、38° B、142° C、152° D、162°8. 如图，直线 ，折线 交 于M，交 于N，点F在 与 之间，设 ， ，则 的度数是
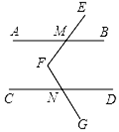A、 B、 C、 D、9. 如图是一块断尺，一块等腰直角三角板的直角顶点刚好落在断尺的下端.则下列结论中，不正确的是（ ）
A、∠1+∠3＝90° B、∠5﹣∠2＝90° C、∠2+∠3+∠4+∠5＝270° D、∠5﹣∠3＝90°10. 如图，AB∥EF，用含∠1，∠2，∠3的式子表示∠4，则∠4等于（ ）
A、∠1+∠2-∠3 B、∠1+∠3-∠2 C、180°+∠3-∠1-∠2 D、∠2+∠3-∠1-180°二、填空题
-
11. 如图所示，直线 ，三角板的直角顶点 落在直线 上，两条直角边分別交直线 于B，C两点.若 ，则 .
12. 如图，直线MN分别与直线AB ， CD相交于点E ， F ， EG平分∠BEF ， 交直线CD于点G ， 若∠MFD＝∠BEF＝62°，射线GP⊥EG于点G ， 则∠PGF的度数为度．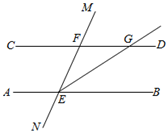
13. 如下图，AB∥EF∥CD，∠ABC=46°，∠BCE=20°，则∠CEF=
14. 已知∠A与∠B（ ， ）的两边-边平行，另一边互相垂直，且 ，则∠A的度数为°.15. 若∠α与∠β的两边分别平行，且∠a=(2x+10)°，∠β=(3x-20)°，则∠a的度数为。16. 如图，直线 ，直线 交 ， 于 ， 两点， 交直线 于点 ，若 ，则 ．
三、综合题
-
17. 已知：如图，三角形ABC中，AC⊥BC ． F是边AC上的点，连接BF ， 作EF∥BC且交AB于点E ． 过点E作DE⊥EF ， 交BF于点D ．
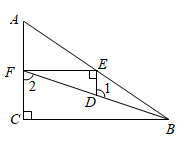
求证：∠1+∠2＝180°．
下面是证明过程，请在横线上填上适当的推理结论或推理依据．
证明：
∵AC⊥BC（已知），
∴∠ACB＝90°（垂直的定义）．
∵EF∥BC（已知），
∴∠AFE＝▲ ＝90°（ ▲）．
∵DE⊥EF（已知），
∴∠DEF＝90°（垂直的定义）．
∴∠AFE＝∠DEF（等量代换），
∴▲∥▲（ ▲）．
∴∠2＝∠EDF（ ▲）．
又∵∠EDF+∠1＝180°（邻补角互补），
∴∠1+∠2＝180°（等量代换）．
18. 如图，在△ABC中，D，E，F分别是三边上的点，且DE平分∠ADF，∠ADF=2∠DFB。
(1)、判断DE与BC是否平行，并说明理由。(2)、若EF//AB，∠DFE=4∠CFE，求∠ADE的度数。19. 如图，已知 平分 交 于点E， .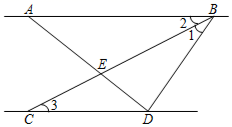
(1)、证明：(2)、若 于点D， ，求 的度数.20. 如图，已知ABCD，E是直线AB上的一点，CE平分∠ACD，射线CF⊥CE，∠1＝32°，
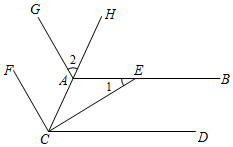(1)、求∠ACE的度数；(2)、若∠2＝58°，求证：CFAG.
