2021-2022学年浙教版七年级下册期中复习专题4 平移
试卷更新日期:2022-03-31 类型:复习试卷
一、单选题
-
1. 以下现象中,属于平移的是( )
①小朋友荡秋千的过程;②电梯上升的过程;③宇宙中行星的运动;④生产过程中传送带上的电视机的移动过程.
A、①② B、②④ C、②③ D、③④2. 下列图形中,周长最长的是( )A、 B、
B、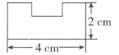 C、
C、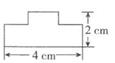 D、
D、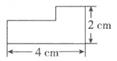 3. 如图 沿直线m向右平移 ,得到 ,下列说法错误的是( )
3. 如图 沿直线m向右平移 ,得到 ,下列说法错误的是( )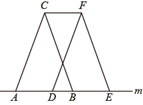 A、 B、 C、 D、4. 将点A(﹣4,﹣1)先向右平移3个单位,再向上平移5个单位得到点A1 , 则点A1的坐标为( )A、(﹣1,4) B、(﹣7,4) C、(﹣1,﹣6) D、(1,﹣4)5. 如图,不是平移设计的是( )A、
A、 B、 C、 D、4. 将点A(﹣4,﹣1)先向右平移3个单位,再向上平移5个单位得到点A1 , 则点A1的坐标为( )A、(﹣1,4) B、(﹣7,4) C、(﹣1,﹣6) D、(1,﹣4)5. 如图,不是平移设计的是( )A、 B、
B、 C、
C、 D、
D、 6. 在数轴上,点 , 在原点 的同侧,分别表示数 ,3,将点 向左平移5个单位长度得到点 ,若点 与点 所表示的数互为相反数,则 的值为( )A、2 B、3 C、 D、07. 如图所示,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,最近的路线是( )
6. 在数轴上,点 , 在原点 的同侧,分别表示数 ,3,将点 向左平移5个单位长度得到点 ,若点 与点 所表示的数互为相反数,则 的值为( )A、2 B、3 C、 D、07. 如图所示,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,最近的路线是( )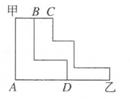 A、①最近 B、①②最近 C、①③最近 D、①②③一样近8. 如图,图中的小三角形可以由三角形ABC平移得到的有( )
A、①最近 B、①②最近 C、①③最近 D、①②③一样近8. 如图,图中的小三角形可以由三角形ABC平移得到的有( ) A、5个 B、6个 C、7个 D、8个9. 如图,点A、B的坐标分别是为 , , 若将线段平移至的位置,与坐标分别是和 , 则线段在平移过程中扫过的图形面积为( )
A、5个 B、6个 C、7个 D、8个9. 如图,点A、B的坐标分别是为 , , 若将线段平移至的位置,与坐标分别是和 , 则线段在平移过程中扫过的图形面积为( ) A、18 B、20 C、28 D、3610. 将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内(相同纸片之间不重叠),其中AB=a.小明发现:通过边长的平移和转化,阴影部分⑤的周长与正方形①的边长有关,那么阴影部分⑥与阴影部分⑤的周长之差与正方形( )(填编号)的边长有关.
A、18 B、20 C、28 D、3610. 将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内(相同纸片之间不重叠),其中AB=a.小明发现:通过边长的平移和转化,阴影部分⑤的周长与正方形①的边长有关,那么阴影部分⑥与阴影部分⑤的周长之差与正方形( )(填编号)的边长有关.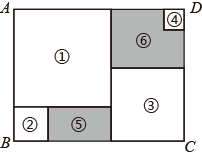 A、① B、② C、③ D、④
A、① B、② C、③ D、④二、填空题
-
11. 如图,是由通过平移得到,且点在同一条直线上,如果 , . 那么这次平移的距离是 .
 12. 如图,将边长为5cm的等边△ABC向右平移1cm,得到△A′B′C′,此时阴影部分的周长为cm.
12. 如图,将边长为5cm的等边△ABC向右平移1cm,得到△A′B′C′,此时阴影部分的周长为cm. 13. 如图所示,长方形ABCD的边长AB=6,BC= 8.则图中五个小长方形的周长之和为
13. 如图所示,长方形ABCD的边长AB=6,BC= 8.则图中五个小长方形的周长之和为 14. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到 ,连接 ,则 的周长为 .
14. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到 ,连接 ,则 的周长为 . 15. 夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为800m,且桥宽忽略不计,则小桥的总长为m.
15. 夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为800m,且桥宽忽略不计,则小桥的总长为m. 16.
16.如图所示,一座楼房的楼梯,高1米,水平距离是2.8米,如果要在台阶上铺一种地毯,那么至少要买这种地毯米.

三、解答题
-
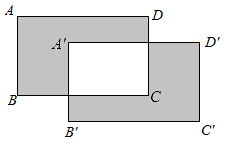
17. 如图,将长为 , 宽为的长方形先向右平移 , 再向下平移 , 得到长方形 , 则阴影部分的面积为多少 .
 18. 某公园有很多的长方形草地,草地里修了很多有趣.的小路,如图三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
18. 某公园有很多的长方形草地,草地里修了很多有趣.的小路,如图三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米. (1)、如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为平方米;(2)、如图2,有两条宽均为1米的小路(图中阴影部分),则草地的面积为平方米;(3)、如图3,非阴影部分为1米宽的小路,沿着小路的中间从人口E处走到出口F处,所走的路线(图中虚线)长为米。19. 如图,把一根木棒放在数轴上,数轴的1个单位长度为1 cm,木棒的左端点与数轴上的点A重合,右端点与点B重合.
(1)、如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为平方米;(2)、如图2,有两条宽均为1米的小路(图中阴影部分),则草地的面积为平方米;(3)、如图3,非阴影部分为1米宽的小路,沿着小路的中间从人口E处走到出口F处,所走的路线(图中虚线)长为米。19. 如图,把一根木棒放在数轴上,数轴的1个单位长度为1 cm,木棒的左端点与数轴上的点A重合,右端点与点B重合. (1)、若将木棒沿数轴水平向右移动,则当它的左端点移动到点B处时,它的右端点在数轴上所对应的数为20;若将木棒沿数轴水平向左移动,则当它的右端点移动到点A处时,它的左端点在数轴上所对应的数为5,由此可得到木棒的长为cm.(2)、图中点A表示的数是 , 点B表示的数是 .(3)、根据(1)(2),请你借助“数轴”这个工具帮助小红解决下列问题:
(1)、若将木棒沿数轴水平向右移动,则当它的左端点移动到点B处时,它的右端点在数轴上所对应的数为20;若将木棒沿数轴水平向左移动,则当它的右端点移动到点A处时,它的左端点在数轴上所对应的数为5,由此可得到木棒的长为cm.(2)、图中点A表示的数是 , 点B表示的数是 .(3)、根据(1)(2),请你借助“数轴”这个工具帮助小红解决下列问题:一天,小红问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”请求出爷爷现在多少岁了.
20. 如图,AD∥BC,∠B=∠D=50°,点E、F在BC上,且满足∠CAD=∠CAE,AF平分∠BAE.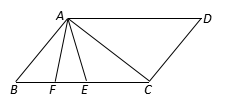 (1)、∠CAF=°;(2)、若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;(3)、在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.21. 在数轴上,点 向右移动1个单位得到点 ,点 向右移动 ( 为正整数)个单位得到点 ,点 , , 分别表示有理数 , , .(1)、当 时,点 , , 三点在数轴上的位置如图所示, , , 三个数的乘积为负数.
(1)、∠CAF=°;(2)、若平行移动CD,那么∠ACB与∠AEB度数的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;(3)、在平行移动CD的过程中,是否存在某种情况,使∠AFB=∠ACD?若存在,求出∠ACD度数;若不存在,说明理由.21. 在数轴上,点 向右移动1个单位得到点 ,点 向右移动 ( 为正整数)个单位得到点 ,点 , , 分别表示有理数 , , .(1)、当 时,点 , , 三点在数轴上的位置如图所示, , , 三个数的乘积为负数.
数轴上原点的位置可能( )
A、在点 左侧或在 , 两点之间 B、在点 右侧或在 , 两点之间 C、在点 左侧或在 , 两点之间 D、在点 右侧或在 , 两点之间(2)、若这三个数的和与其中的一个数相等,则(3)、将点 向右移动 个单位得到点 ,点 表示有理数 , 、 、 、 四个数的积为正数,这四个数的和与其中的两个数的和相等,且 为整数请用含 的代数式表示 ,写出推理过程.