2021-2022学年浙教版七年级下册期中复习专题1 平行线

试卷更新日期：2022-03-31 类型：复习试卷

进入出卷网下载

一、填空题

1. 在同一，的两条直线叫做平行线．有时我们说两条射线或两条线段平行，实际上是指它们所在的直线平行

查看试题解析
2. 已知a、b是同一平面内的任意两条直线．

(1)、若直线a、b没有公共点，则直线a、b的位置关系是

(2)、若直线a、b有且只有一个公共点，则直线a、b的位置关系是；

(3)、若直线a、b有两个以上的公共点，则直线a、b的位置关系是．

查看试题解析

二、单选题

3. 下列说法中，不正确的是（）

A、过任意一点可作已知直线的一条平行线 B、同一平面内两条不相交的直线是平行线 C、在同一平面内，过直线外一点只能画一条直线与已知直线垂直 D、平行于同一直线的两直线平行

查看试题解析
4. 在同一平面内，两条不重合的直线的位置关系可能是（）

A、平行或相交 B、垂直或相交 C、垂直或平行 D、平行、垂直或相交

查看试题解析
5.
如图，已知AB⊥CD于O，直线EF经过点O与AB的夹角∠AOE=52°，则∠COF的度数是（　　）

A、52° B、128° C、38° D、48°

查看试题解析
6.
如图，能确定l₁∥l₂的α为（　　）

A、140° B、150° C、130° D、120°

查看试题解析
7. 直线a、b、c是三条平行直线．已知a与b的距离为5cm，b与c的距离为2cm，则a与c的距离为（　　）

A、2cm B、3cm C、7cm D、3cm或7cm

查看试题解析
8.
如图，在立定跳远中，体育老师是这样测量运动员的成绩的，用一块直角三角板的一边附在起跳线上，另一边与拉直的皮尺重合，这样做的理由是（　）

A、两点之间线段最短 B、过两点有且只有一条直线 C、垂线段最短 D、过一点可以作无数条直线

查看试题解析
9.
如图，直线AB、CD、EF相交于点O，则∠1+∠2+∠3的度数为（　　）

A、90° B、120° C、180° D、不能确定

查看试题解析
10. a，b，c是同一平面内任意三条直线，交点可能有（）

A、1个或2个或3个 B、0个或1个或2个或3个 C、1个或2个 D、都不对

查看试题解析
11. 已知n（n≥3，且n为整数）条直线中只有两条直线平行，且任何三条直线都不交于同一个点．如图，当n=3时，共有2个交点；当n=4时，共有5个交点；当n=5时，共有9个交点；…依此规律，当共有交点个数为27时，则n的值为（）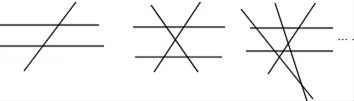

A、6 B、7 C、8 D、9

查看试题解析
12. 按下所语句画图：点M在直线a上，也在直线b上，但不在直线c上，直线a，b，c两两相交，下图中正确的是（）

A、 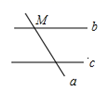B、 C、 D、

查看试题解析

三、解答题

13. 尺规作图（不写作法，请保留作图痕迹）
已知：点 $P$ 为直线 $A B$ 外一点，求作：直线 $P Q$ ，使得 $P Q ∥ A B$ ．

查看试题解析
14. 根据下列要求画图．

(1)、如图1所示，过点A画MN∥BC；

(2)、如图2所示，三条直线a，b，c两两相交，点P在三条直线围成的三角形外，过点P画l₁∥a交直线6于点Q，过点Q画直线l₂∥c交直线a于点M．

查看试题解析
15. 如图，在8×6的正方形网格中，每个小正方形的顶点称为格点，点D是∠ABC的边BC上的一点，点M是∠ABC内部的一点，点A、B、C、D、M均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，并回答问题：

(1)、过点M画BC的平行线MN交AB于点N；

(2)、过点D画BC的垂线DE，交AB于点E；

(3)、点E到直线BC的距离是线段的长度．

查看试题解析
16. 任选一题作答，只计一题的成绩：

(1)、如图，在 $6 \times 5$ 的正方形网格中，点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ 都在格点上.连接点 $A$ ， $B$ 得线段 $A B$ .

Ⅰ.画出过 $C$ ， $D$ ， $E$ ， $F$ 中的任意两点的直线；

Ⅱ.互相平行的直线（线段）有▲ ；（请用“ $∥$ ”表示）

Ⅲ.互相垂直的直线（线段）有▲ .（请用“ $⊥$ ”表示）

(2)、如图，直线 $A B$ 和 $C D$ 相交于 $O$ ， $∠ E O C = 90 °$ ， $O F$ 是 $∠ A O E$ 的角平分线， $∠ C O F = 34 °$ ，求 $∠ B O D$ 的度数.

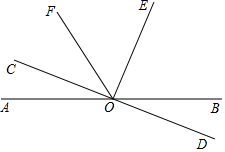
其中一种解题过程如下，请在括号中注明根据，在横线上补全步骤.

解： $∵ ∠ E O C = 90 °$

$∠ C O F = 34 °$ $($ ▲ $)$

$∴ ∠ E O F =$ ▲ $°$

$∵ O F$ 是 $∠ A O E$ 的角平分线

$∴ ∠ A O F =$ ▲ $= 56 °$ $($ ▲ $)$

$∴ ∠ A O C =$ ▲ $°$

$∵ ∠ A O C +$ ▲ $= 90 °$

$∠ B O D + ∠ E O B = 90 °$ $($ ▲ $)$

$∴ ∠ B O D = ∠ A O C =$ ▲ $°$ $($ ▲ $)$

查看试题解析
17. 如图

如图1，已知直线m∥n，点A，B在直线n上，点C，P在直线m上。

(1)、写出图1中面积相等的各对三角形：。

(2)、如图1，A，B，C为三个顶点，点P在直线m上移动到任一位置时，总有与△ABC的面积相等。

(3)、如图2，一个五边形ABCDE，你能否过点E作一条直线交BC（或BC的延长线）于点M，使四边形ABME的面积等于五边形ABCDE的面积？

查看试题解析